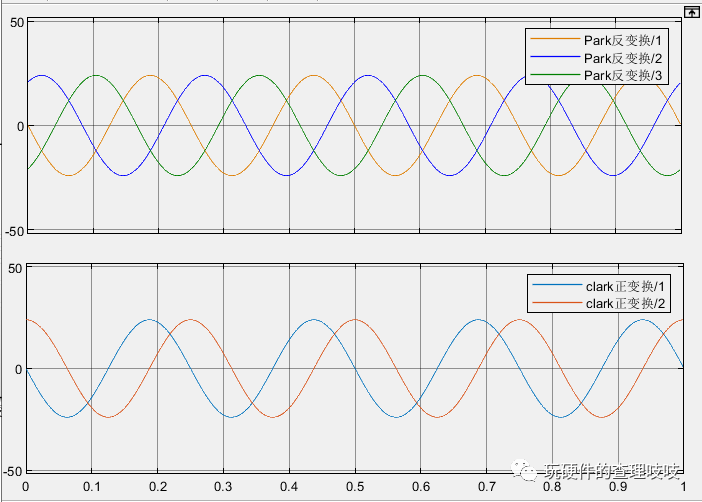
通过Clarke变换后所得到的α、β静止坐标系上的分量，我们要注意现在得到的还是正弦信号，既不是阶跃信号，也不是斜坡信号。

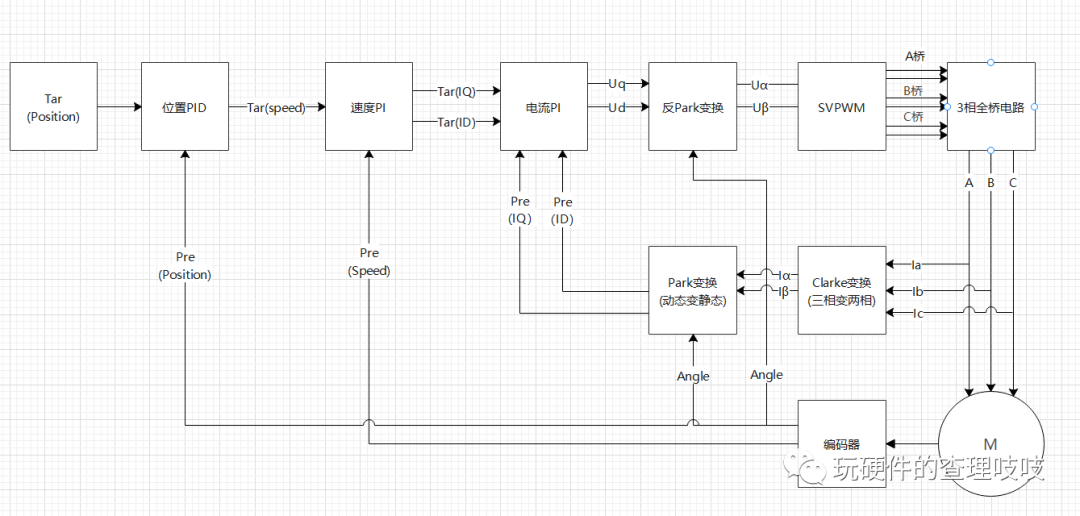
目前的主要控制方法是以PI控制器为主。然而PI控制器只能实现直流信号的无稳态误差的跟踪，当它跟踪正弦波信号时，必然出现不稳定的稳态误差。那么为了实现对α、β轴分量的无稳态误差控制，主要有两种方向：

一是设计一种能够对正弦波信号无稳态误差的控制器（明显有研究深度，较困难）；

二是将正弦波信号转化为直流信号，从而可以继续采用PI控制器（难度降低）；

显然我们的前辈对PI控制器的参数整定方法已经比较熟悉，因此采用第二种方式将一个新问题转为已解决的问题，可大大简化设计难题，于是Robert H. Park提出了park变换。

如上图所示，合成矢量Vδ在α、β坐标系下的投影 Vα,Vβ 的幅值是正弦变换的。设计 d、q 坐标系，当它与Vδ以相同的角速度旋转时，在d、q轴上的投影Vd,Vq的幅值是恒定的，即相对于选择矢量而言，Vd,Vq为直流量，这样就可沿用PI控制策略进行设计。

具体矩阵算法如下；

依据公式搭建matlab模型，设定矢量旋转的电磁角度θ=0.25s/2pi,仿真出波形如下；

综上介绍了SVPWM的坐标变换，我认为矢量控制的本质即有功和无功的单独控制。而坐标变换，是其实现解耦的方法。矢量控制即“磁场定向控制”，意思就是把磁场方向，定向在一个坐标轴D轴上（人为定义），而转矩的方向与磁场正好垂直，它也就恰好被定向到了Q轴上（人为定义与D轴垂直）。把电机的电流也同样解耦在该DQ坐标轴上，就可以分别转矩与磁场分别解耦控制。