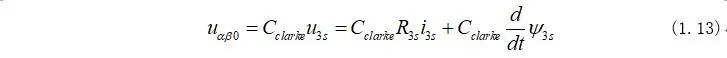Clarke变换是“矢量坐标变换”中的一种变换方式，在永磁同步电机中，电动机的定子磁场是由定子的三相绕组的磁动势产生的，根据电动机旋转磁场理论就知，向对称的三相绕组中通以对称的三相正弦电流时，就会产生合成的磁动势，并以w的速度在空间中旋转。所以，为了简化交流电机的分析方法，Clarke提出了一种以电机定子为静止参考系的电机参数变换分析方式，即依据功率不变和磁势不变的原理，将定子三相物理量从三维坐标转换到二维坐标，简称3S/2S变换，其中S表示静止。

在PMSM中建立合适的坐标系

图1-1中两个坐标系，其中ABC是PMSM静止坐标系，另一个坐标系是PMSM经过Clarke要变换后的坐标系：

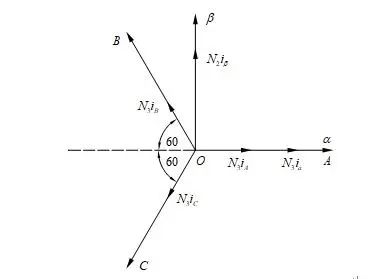
图1-1 Clarke坐标变换示意图

图1-1中PMSM三相绕组每相的有效线圈匝数为N3，两相绕组每相有效线圈匝数为N2，两种坐标系中每相的磁动势均为有效线圈匝数与该相电流的乘积。

原理分析

矢量坐标变换就是用磁势或者电流空间矢量来描述等效的三相磁场、两相磁场和旋转直流磁场，并对它们进行坐标变换。因此矢量坐标变化必须要遵循以下两个原则：

1、变换前后电流所产生的旋转磁场等效;

2、变换前后两系统的电动机功率不发生变化。

根据矢量变换原则，Clarke变换前后的磁场应该完全等效，即合成的磁势矢量分别在两个坐标系坐标轴上的投影应该相等。设磁动势是正弦分布的，当三相总磁动势与两相总磁动势相等时，两套绕组瞬时磁动势在两相坐标系上的投影都应相等。

因此根据图1-1可以得出磁势守恒的式子为：

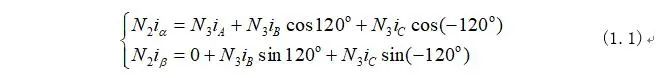
将式(1.1)变形又可化为矩阵形式为：

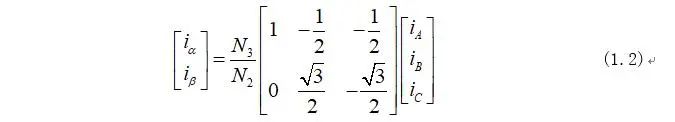
因为式(1.2)中矩阵不是方阵不能求的逆矩阵，所以需要引入新变量零轴电流：

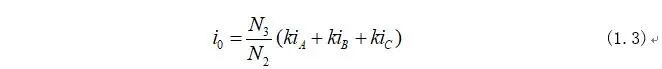
将式(1.3)和式(1.2)合并可以得到两相坐标系方程为：

所以定义Clarke矩阵为：

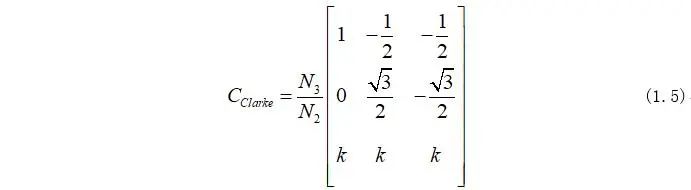
Clarke最终表达形式

其中Clarke矩阵的转置矩阵为：

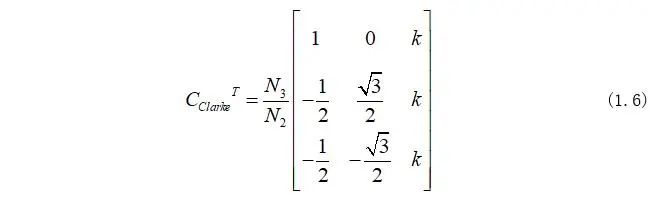
Clarke矩阵的逆矩阵为：

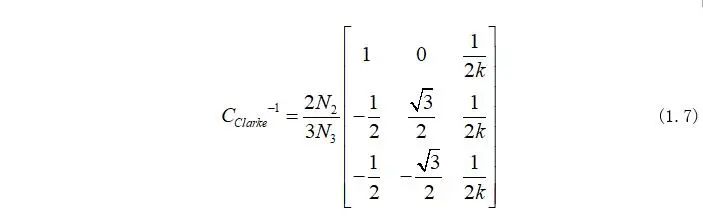
在Clarke变换下需要保证发电机的输出功率在变换前后不能发生变换，因此计算公式为：

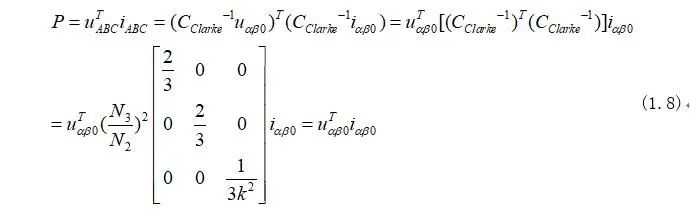
由式(1.8)可知，为了确保变换前后输出功率不变化，可以其中参数求得：

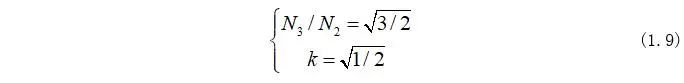
因此，Clarke变换式为：

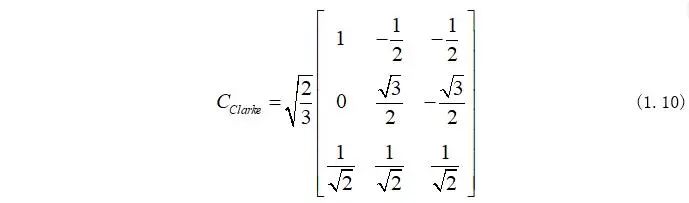
如果忽略零轴变量，那么Clarke变换式又可化为：

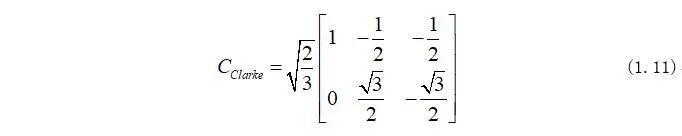
Clarke如何应用

如何得到永磁同步电机在静止两相坐标的电机电压方程?

永磁同步电机的定子电压方程在三相静止坐标系下为：

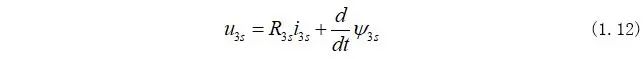
将式(1.12)乘以Clarke矩阵可以得到永磁同步电机在两相静止坐标系下的电机电压方程为：