磁场定向控制中使用到的坐标变换主要有Clark变换、Park变换、Anti-Park变换。其中Clark变换是三相静止绕组A、B、C和两相静止绕组α-β之间的变换；Park变换是两相静止坐标系α-β到两相旋转坐标系d、q之间的变换；Anti-Park变换是Park的逆变换。

本篇文章将讲述Clark变换，从公式推导到仿真实现，最后到C语言代码实现验证Clark变换。

一、Clark坐标变换公式推导

图1 三相和两相坐标系与绕组磁动势的空间矢量

图1中绘出了A、B、C和α-β两个坐标系，为方便起见，取A轴与α轴重合。设三相绕组每相有效匝数为N3，两相绕组每相有效匝数为N2，各相磁动势为有效匝数与电流的乘积，其空间矢量均位于有关相的坐标轴上。由于交流磁动势的大小随时间在变化着，图中磁动势矢量的长度是随意的。

设磁动势波形是正弦分布的，当三相总磁动势与两相总磁动势相等时，两套绕组瞬时磁动势在α、β轴上的投影都应相等，因此：

写成矩阵形式，得：

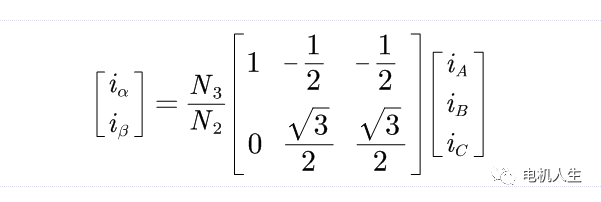
考虑变换前后总功率不变，得：

考虑变换前后幅值不变，得：

上面的变换矩阵即为Clark坐标变换矩阵，在PMSM矢量控制中主要用于将三相电流Ia、Ib、Ic变换成两相电流Ialpha、Ibeta。

二、Clark坐标变换Matlab/Simulink仿真验证

在Simulink中搭建Clark变换，本次仿真中使用的是等幅值变换。

仿真结果为：

三、Clark坐标变换C语言实现

在处理器中编写程序，并放在中断中运行，打印波形，观察Clark变换。实验结果如下：

使用J-Scope打印结果，上面为三相输入，下面为经坐标变换后的输出结果。

四、总结

本篇文章编写了电机矢量控制中使用到的坐标变换之Clark变换，并进行仿真和实验验证。