1、SVPWM原理简介
PWM(Pulse Width Modulation)脉宽调整,这是一种利用面积等效原理实现的控制技术。SVPWM(Space Vector PWM)空间矢量PWM控制,因为控制电动机内部的圆形旋转磁场,最终需要控制的是电压空间矢量。一般控制电机的三相电压相互成120度,以正弦的形式变换。我们需要控制的就是这三相电压呈现这种形式来最终控制到电磁转矩。主电路图如下所示:
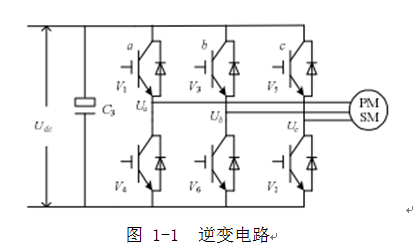
将三相电压矢量以等幅计算方式转换为两相矢量得:
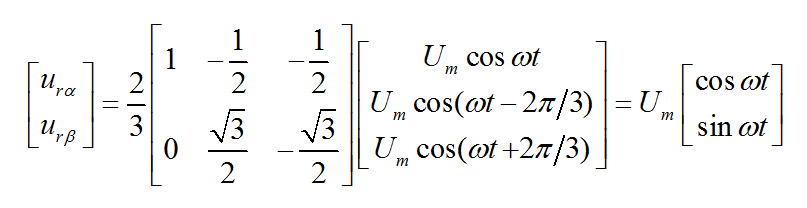
由于逆变器三相桥臂共有6个开关管,为了研究各相上下桥臂不同开关组合时逆变器输出的空间电压矢量,特定义开关函数Sx(x=a、b、c) 为:

(Sa、Sb、Sc)的全部可能组合共有八个,包括6个非零矢量 Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量 U0(000)、U7(111),下面以其中一种开关组合为例分析,假设Sx(x=a、b、c)=(100),此时

求解上述方程可得:UaN=2Ud/3、UbN=-Ud/3、UcN=-Ud/3。同理可计算出其它各种组合下的空间电压矢量,列表如下:
表 1-1 开关状态与相电压和线电压的对应关系
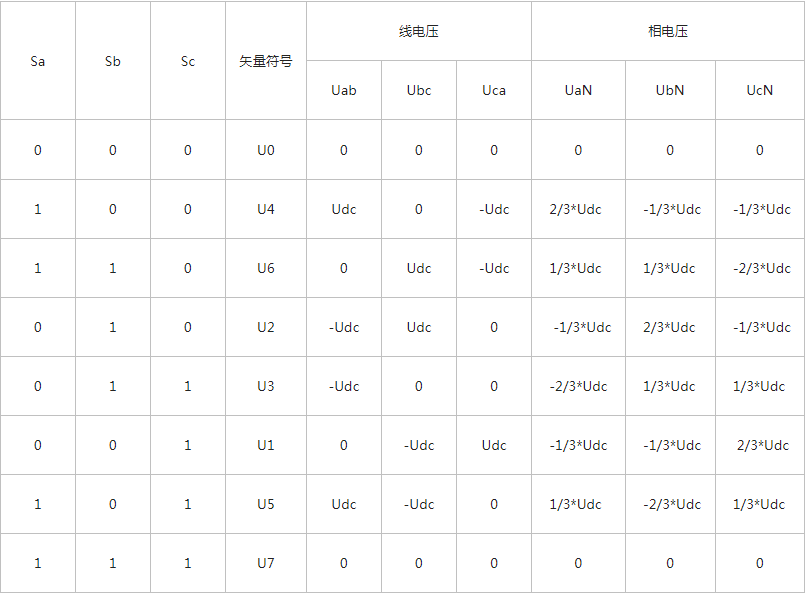
八个基本电压空间矢量的大小和位置入下图所示:

如果某一瞬间要求的电压控制键矢量在第一扇区,那么可以根据第一扇区的矢量U4以及U6以及零矢量U0或U7合成所要求的矢量U。经过计算,可以得到各矢量的状态保持时间为:

式中 m 为 SVPWM 调制系数(调制比):若要求Uref的模保持恒定,则Uref的轨迹为一圆形;若要求三相电压波形不失真(即不饱和),则Uref的轨迹应在正六边形内部;结合此两点可知Uref的模取最大值时的轨迹为正六边形的内切圆,此时m=1,故m<=1。
我们以减少开关次数为目标,将基本矢量作用顺序的分配原则选定为:在每次开关状态转换时,只改变其中一相的开关状态。并且对零矢量在时间上进行了平均分配,以使产生的 PWM对称,从而有效地降低PWM的谐波分量。当 U4(100)切换至 U0(000)时,只需改变 A 相上下一对切换开关,若由 U4(100)切换至 U7(111)则需改变 B、C 相上下两对切换开关,增加了一倍的切换损失。因此要改变电压矢量U4(100)、U2(010)、U1(001)的大小,需配合零电压矢量U0(000),而要改变U6(110)、U3(011)、U5(101),需配合零电压矢量U7(111)。这样通过在不同区间内安排不同的开关切换顺序, 就可以获得对称的输出波形,其它各扇区的开关切换顺序如表 所示:
Uref 所在的位置 |
开关切换顺序 |
三相波形图 |
Ⅰ区(0°≤θ≤60°) |
…0-4-6-7-7-6-4-0… |

|
Ⅱ区(60°≤θ≤120°) |
…0-2-6-7-7-6-2-0… |

|
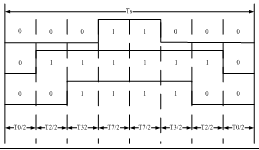
Ⅲ区(120°≤θ≤180°) |
…0-2-3-7-7-3-2-0… |
|
Ⅳ区(180°≤θ≤240°) |
…0-1-3-7-7-3-1-0… |

|
Ⅴ区(240°≤θ≤300°) |
…0-1-5-7-7-5-1-0… |
|
Ⅵ区(300°≤θ≤360°) |
…0-4-5-7-7-5-4-0… |

|
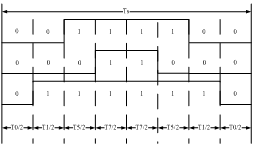
以第Ⅰ扇区为例,其所产生的三相波调制波形在时间 Ts 时段中如图所示,图中电压矢量出现的先后顺序为 U0、U4、U6、U7、U6、U4、U0,各电压矢量的三相波形则与表 1-2 中的开关表示符号相对应。再下一个 TS 时段,Uref 的角度增加一个γ,利用式(1-8)可以重新计算新的 T0、T4、T6 及 T7 值,得到新的合成三相类似表(1-2)所示的三相波形;这样每一个载波周期TS就会合成一个新的矢量,随着θ的逐渐增大,Uref 将依序进入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ区。在电压向量旋转一周期后,就会产生 R 个合成矢量。
通过以上 SVPWM 的法则推导分析可知要实现SVPWM信号的实时调制,首先需要知道参考电压矢量 Uref 所在的区间位置,然后利用所在扇区的相邻两电压矢量和适当的零矢量来合成参考电压矢量。图1-4是在静止坐标系(α,β)中描述的电压空间矢量图,电压矢量调制的控制指令是矢量控制系统给出的矢量信号 Uref,它以某一角频率ω在空间逆时针旋转,当旋转到矢量图的某个 60°扇区中时,系统计算该区间所需的基本电压空间矢量,并以此矢量所对应的状态去驱动功率开关元件动作。当控制矢量在空间旋转 360°后,逆变器就能输出一个周期的正弦波电压。
空间矢量调制的第一步是判断由 Uα 和 Uβ所决定的空间电压矢量所处的扇区。假定合成的电压矢量落在第 I 扇区,可知其等价条件如下:

以上等价条件再结合矢量图几何关系分析,可以判断出合成电压矢量 Uref 落在第 X扇区的充分必要条件,得出下表:
扇区 |
落在此扇区的充要条件 |
I |
Uα>0 ,Uβ>0 且Uβ/ Uα |
Ⅱ |
Uα>0 , 且Uβ/ |Uα|>sqrt(3) |
Ⅲ |
Uα<0 ,Uβ>0 且-Uβ/ Uα |
Ⅳ |
Uα<0 ,Uβ<0 且Uβ/ Uα |
Ⅴ |
Uβ<0 且-Uβ/|Uα|>sqrt(3) |
Ⅵ |
Uα>0 ,Uβ<0 且-Uβ/Uα |
若进一步分析以上的条件,有可看出参考电压矢量Uref 所在的扇区完全由Uβ, sqrt(3)Uα-Uβ, -sqrt(3)Uα- Uβ 三式决定,因此令:

再定义,若U1>0 ,则 A=1,否则 A=0; 若U 2>0 ,则 B=1,否则 B=0;若U3>0 ,则 C=1,否则 C=0。可以看出 A,B,C 之间共有八种组合,但由判断扇区的公式可知 A,B,C 不会同时为 1 或同时为 0,所以实际的组合是六种,A,B,C 组合取不同的值对 应着不同的扇区,并且是一一对应的,因此完全可以由 A,B,C 的组合判断所在的扇区。为区别六种状态,令 N=4*C+2*B+A,则可以通过下表计算参考电压 矢量 Uref 所在的扇区。
N值与扇区对应关系
N |
3 |
1 |
5 |
4 |
6 |
2 |
扇区号 |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅳ |
Ⅴ |
Ⅵ |
采用上述方法,只需经过简单的加减及逻辑运算即可确定所在的扇区,对于提高系统的响应速度和进行仿真都是很有意义的。
最后因为程序中控制的是没相电压的占空比,占空比经过计算得到如下表格
表 1-4 各扇区基本空间矢量的作用时间
扇区 |
时间 |
|
I |
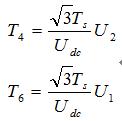
|
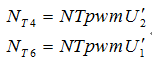
|
Ⅱ |

|
 |
Ⅲ |

|
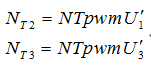
|
Ⅳ |
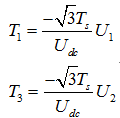
|

|
Ⅴ |
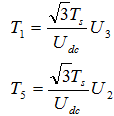
|

|
Ⅵ |

|

|
在扇区1中时间图如下:
2、stm32f427资源简介
a、 stm32f427带有FPU,它有硬件的浮点计算器,所以执行SVPWM算法大致需要15us左右的时间
b、stm32f427的定时器1有7路PWM端口,其中6路是互补的PWM可以实现对三相桥式电路的控制,另外一路PWM端口,用来指示采样电流的时间。
c、stm32f427有多路ADC转换,并且分为注入组与规则组,注入组的优先级高于规则组。SPWM算法就是在采样相电流完成后处理的。
d、采样相电流的时间:这里采用的是双电阻采样法,采样的时间是三相PWM都为0的时候,这时候的电流状态如图所示,这时候采样电阻上的电流就是相电流。现在的关键点是怎么知道是处于零矢量的状态,其实设置定时器1的PWM4占空是4路PWM中最高的就可以了,当然还需要考虑ADC的转换时间,这有个坏处就是PWM占空比将不能达到最大。
3、SVPWM算法程序实现
需要用到的结构体如下
struct CLARK
{
long Ia; //输入,A相定子电流
long Ib; //输入,B相定子电流
long Ic; //输入,C相定子电流
long IAlpha; //输出,静止坐标系Alpha轴定子电流
long IBeta; //输出,静止坐标系Beta轴定子电流
void (*calcClark)();
void (*calcAntiClark)();
};
struct PARK
{
long Id; //输出,旋转坐标系下的D坐标值电流
long Iq; //输出,旋转坐标系下的Q坐标值电流
long IAlpha; //输入,静止坐标系Alpha轴定子电流
long IBeta; //输入,静止坐标系Beta轴定子电流
float Ud; //输出,旋转坐标系下的D坐标值电压
float Uq; //输出,旋转坐标系下的Q坐标值电压
float UAlpha; //输入,静止坐标系Alpha轴定子电压
float UBeta; //输入,静止坐标系Beta轴定子电压
long Theta; //旋转坐标角度
float ActId; //实际D轴电流
float ActIq; //实际Q轴电流
void (*calcPark)();
void (*calcAntiPark)();
};
struct SVPWM
{
float UAlpha; //输入,静止坐标系Alpha轴定子电压
float UBeta; //输入,静止坐标系Beta轴定子电压
long Ua; //
long Ub; /
long Uc; //
long Tx; //
long Ty; //
long Tz; //
long taOn; //A相时间
long tbOn; //B相时间
long tcOn; //C相时间
};
1、clark变换模块程序,clark变换既将三相坐标系转换成二相固定坐标系的变换。
static void Clark_calc(struct CLARK *v)
{
float sqrt_3 = SQRT_3;//添加浮点变量为了编译器优化调用硬件浮点指令
v->IAlpha = v->Ia;
v->IBeta = (sqrt_3/3)*(v->Ia+(v->Ib*2));
}
2、park变换模快程序,park变换既二相固定坐标系转换成二相旋转坐标系的变换。存在旋转坐标系是为了将永磁同步电机的励磁电流与转矩电流剥离。
#define SinPointNum 3600
extern const int Sin_Table[SinPointNum];//正弦表
static void Park_Calc(struct PARK *v)
{
long Sinthe,Costhe;
UINT16 Point;
Point = v->Theta;
if(Point<2700)
Costhe = Sin_Table[Point+900];
else
Costhe = Sin_Table[Point-2700]; // Ualpha = Ucos(the) UpmMax = 2/3Udc
Sinthe = Sin_Table[Point]; // Ubeta = Usin(the)
v->Id = v->IAlpha*Costhe+v->IBeta*Sinthe;
v->Iq = -v->IAlpha*Sinthe+v->IBeta*Costhe;
v->Id = v->Id/0x8000;
v->Iq = v->Iq/0x8000;
v->ActId = (float)(v->Id)*7.15*3.3/4096;//最大采样实际电流11.8a
v->ActIq = (float)(v->Iq)*7.15*3.3/4096;//最大采样实际电流11.8a
}
3、反park变换,反park变换既二相旋转坐标系转换成二相固定坐标系的变换
static void Anti_Park_Calc(struct PARK *v)
{
int Sinthe,Costhe;
UINT16 Point;
Point = v->Theta;
if(Point<2700)
Costhe = Sin_Table[Point+900];
else
Costhe = Sin_Table[Point-2700]; // Ualpha = Ucos(the) UpmMax = 2/3Udc
Sinthe = Sin_Table[Point]; // Ubeta = Usin(the)
v->UAlpha = v->Ud*(float)Costhe - v->Uq*(float)Sinthe;//范围是-sqrt(2)μ?+sqrt(2)
v->UBeta = v->Ud*(float)Sinthe + v->Uq*(float)Costhe;//范围是-sqrt(2)μ?+sqrt(2)
}
4、SVPWM模块实现
static void Svpwm_Module(struct SVPWM *pstrSvpwm)
{
UINT8 u8Sector=0;
UINT8 a,b,c;
int t1,t2;
int temp;
float sqrt_3 = SQRT_3;//添加浮点变量为了编译器优化调用硬件浮点指令
float m = K;
UINT8 Udc = MOTOR_POWER;
/* 利用以下公式确定扇区 */
// iClarkBeta_calc(&strSvpwm.v);
// pstrSvpwm->v.Va = pstrSvpwm->v.Beta; // beta
// pstrSvpwm->v.Vb = (AMP1000_SQRT_3*pstrSvpwm->v.Alpha/2 - pstrSvpwm->v.Beta*AMP1000/2)/AMP1000; // alpha*sqrt(3/4)-0.5*beta
// pstrSvpwm->v.Vc = (-AMP1000_SQRT_3*pstrSvpwm->v.Alpha/2 - pstrSvpwm->v.Beta*AMP1000/2)/AMP1000; // -alpha*sqrt(3/4)-beta*0.5
pstrSvpwm->Ua = pstrSvpwm->UBeta; // beta
pstrSvpwm->Ub = (sqrt_3*pstrSvpwm->UAlpha/2 - pstrSvpwm->UBeta/2); // alpha*sqrt(3)-beta
pstrSvpwm->Uc = (-sqrt_3*pstrSvpwm->UAlpha/2 - pstrSvpwm->UBeta/2); // -alpha*sqrt(3)-beta
if(pstrSvpwm->Ua>0)
a = 1;
else
a = 0;
if(pstrSvpwm->Ub>0)
b = 1;
else
b = 0;
if(pstrSvpwm->Uc>0)
c = 1;
else
c = 0;
u8Sector = 4*c + 2*b + a;
//*24/MOTOR_POWER
/* 利用下面公式计算出X、Y、Z 其中Ts为Timer1_Period,Udc为MOTOR_POWER*/
pstrSvpwm->Ua = sqrt_3*pstrSvpwm->Ua/Udc*Ts/(0x8000);//X=sqrt(3)*beta*Ts/Udc
pstrSvpwm->Ub = sqrt_3*pstrSvpwm->Ub/Udc*Ts/(0x8000);//Y=(sqrt(3)/2*beta+3/2*alpha)*Ts/Udc
pstrSvpwm->Uc = sqrt_3*pstrSvpwm->Uc/Udc*Ts/(0x8000);//Z=(sqrt(3)/2*beta-3/2*alpha)*Ts/Udc
// pstrSvpwm->v.Va = SQRT_3*pstrSvpwm->v.Va*Ts/(0x8000)*K;//X=sqrt(3)*beta*Ts/Udc
// pstrSvpwm->v.Vb = SQRT_3*pstrSvpwm->v.Vb*Ts/(0x8000)*K;//Y=(sqrt(3)/2*beta+3/2*alpha)*Ts/Udc
