现今随着高端测试仪器和仿真软件的普及,大部分的损耗计算都可以使用工具自动完成,节省了不少精力,不得不说这对工程师来说是一种解放,但是这些工具就像黑盒子,好学的小伙伴总想知道工作机理。其实基础都是大家学过的基本高等数学知识。今天作者就帮大家打开这个黑盒子,详细介绍一下损耗计算方法同时一起复习一下高等数学知识。
本文引用地址:我们先来看一个的完整工作波形:
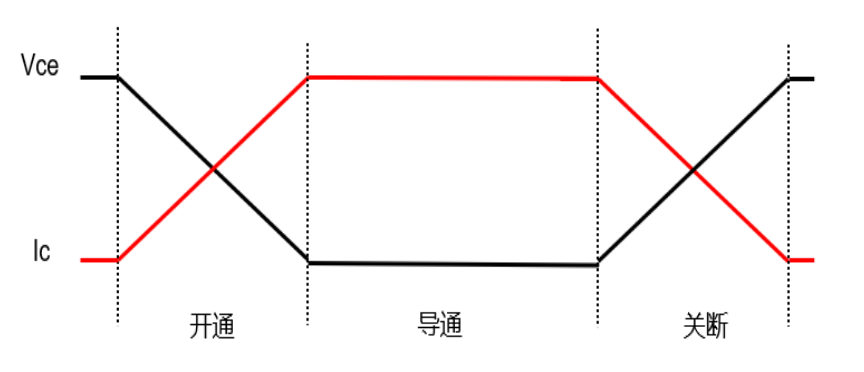
的损耗可以分为开关损耗和导通损耗,其中开关损耗又分为开通和关断两部分,下面我分别来看一下各部分的计算推导过程。
开关损耗-开通部分
我们先来看一下理想的IGBT开通波形:
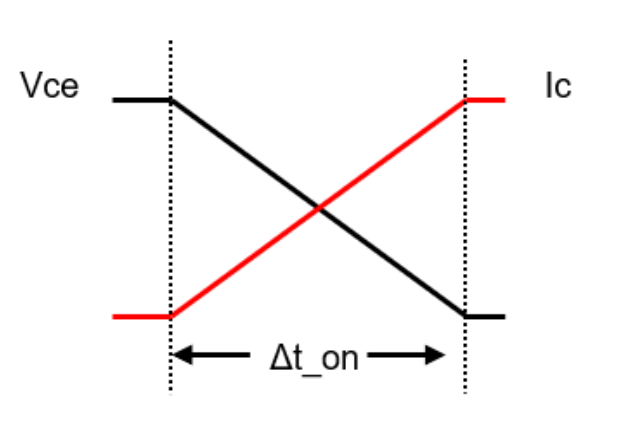
我们需要先分别写出电流和电压的线性方程,先看电流线性方程:分别找到电流开关波形中的两个坐标(0,0) 和 (Δt_on, Ic) , 那么电流线性方程:
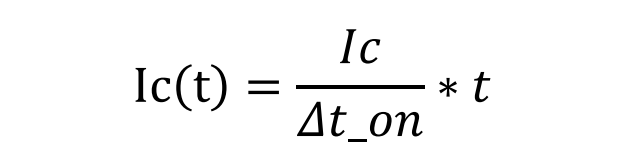
电压线性方程,同样找到电压波形中的两个坐标(0,Vce), (Δt-on,0),那么电压线性方程:
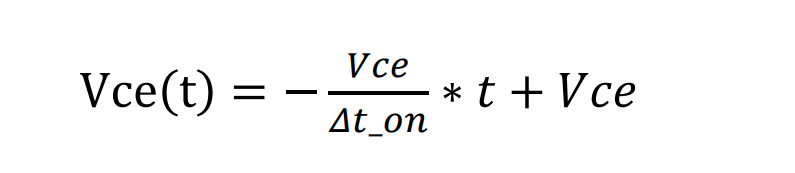
根据损耗计算的定义:

这样开关损耗中的开通部分计算公式我们就推导完成了,那是不是我们有了计算公式就可以直接用了呢?我们先来看看实际的开通波形:
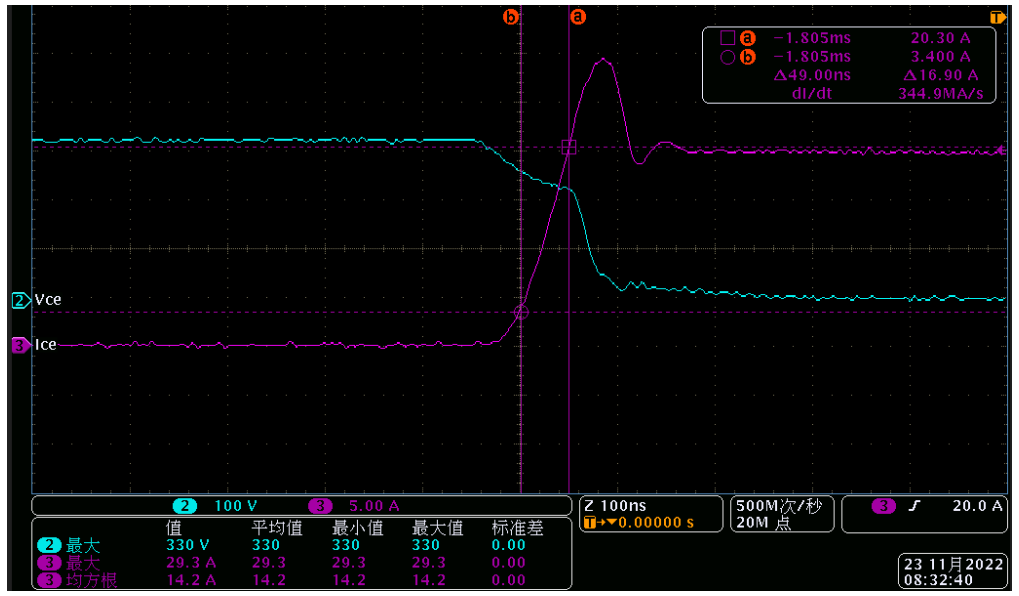
上图是实测的IGBT开通波形,蓝色是Vce波形,红色是Ic波形。可以看到Ic在整个上升过程中还是比较线性的,但是Vce在跌落的时候斜率分成了几段,这个时候我们推导的理想开关波形的损耗似乎就没什么用了,那怎么办呢?
其实虽然我们之前的推导结果不能直接用,但是推导过程我们还是可以借鉴的,我们可以把整个波形根据Vce 的斜率分成几个部分来近似计算,如下图所示,对应时间分别是Δt1, Δt2, Δt3。
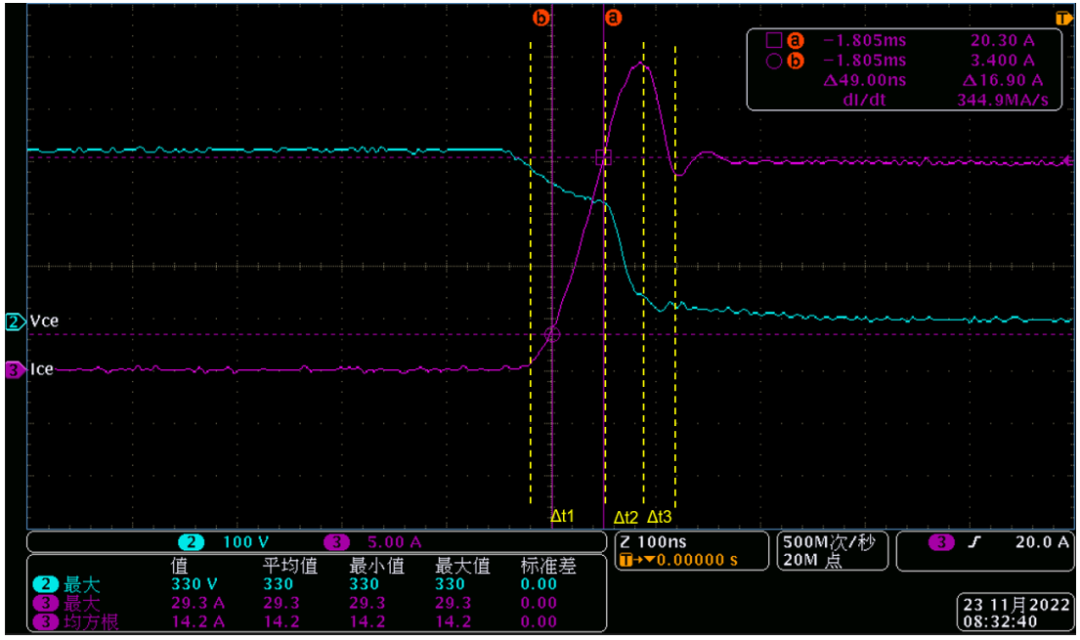
我们先来计算Δt1部分的损耗:
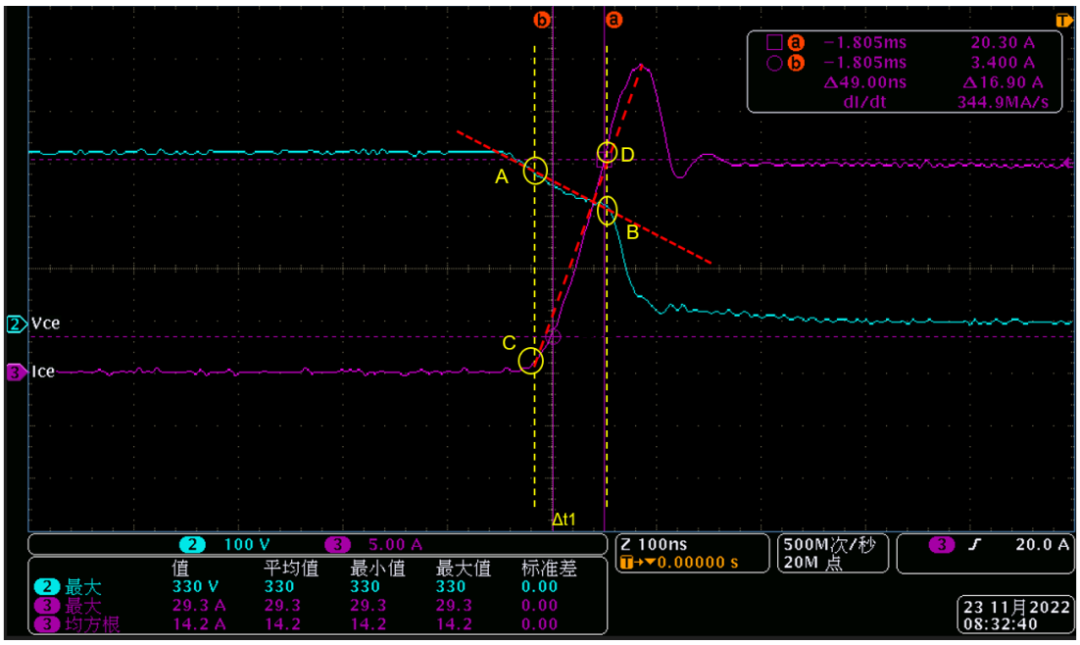
如上图,我们先找到电压和电流波形与Δt1时间标注线的四个交点,标注为:
A(0,Vce1), B(Δt1,Vce2), C(0,0), D(Δt1,Ic1).
Δt1内的Vce表达式:
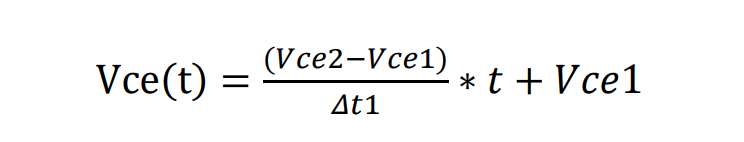
Δt1内的Ic表达式:
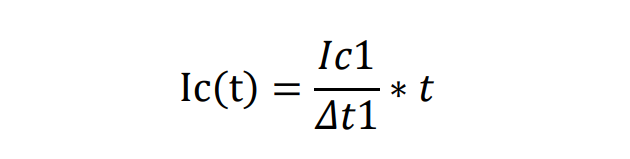
Δt1内的损耗表达式及推导:
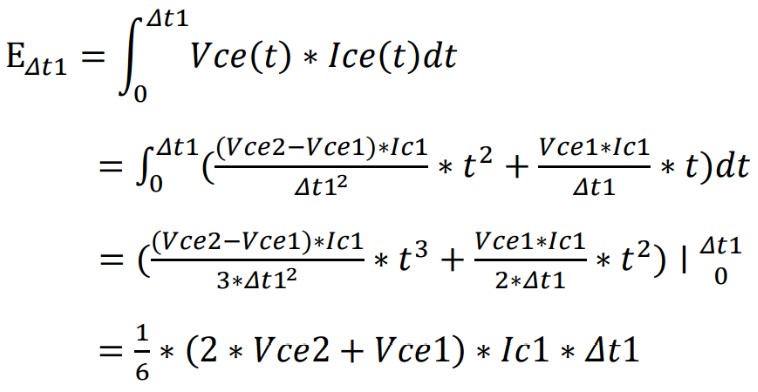
从波形中可以读出:
Vce1=260V, Vce2=220V, Ic1=20.3A, Δt1=70ns, 带入上面公式可以得到:
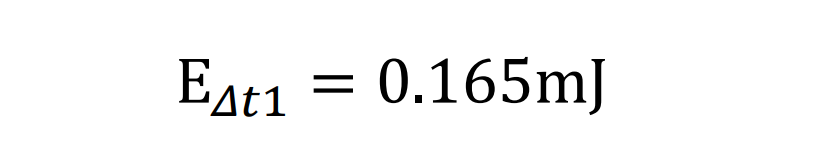
我们用同样的方法计算Δt2部分:
同样先找到电压和电流波形与Δt2时间标注线的四个交点:
E(0,Vce2), F(Δt2,Vce3), G(0,Ic1), H(Δt2,Ic2).
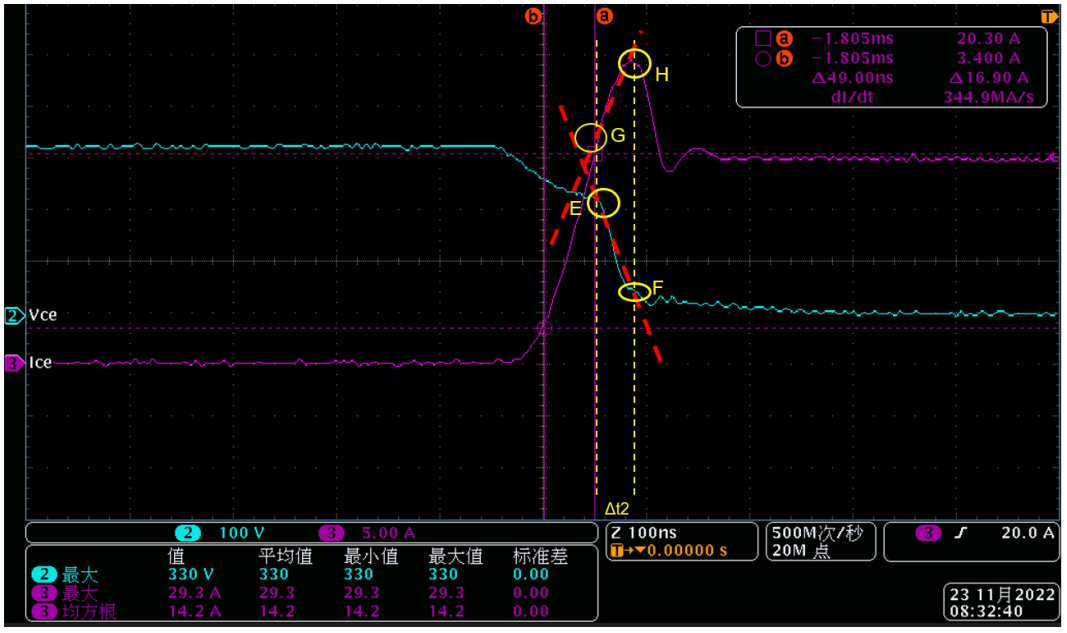
Δt2内的Vce表达式:
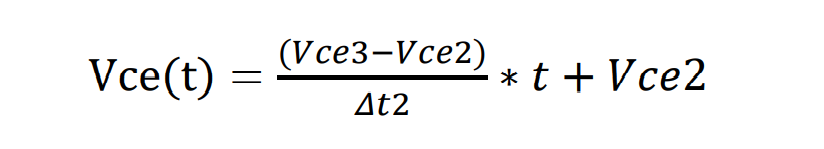
Δt2内的Ic表达式:
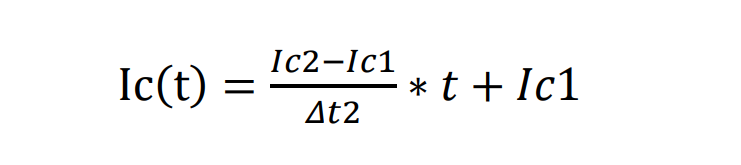
Δt2内的损耗表达式及推导:
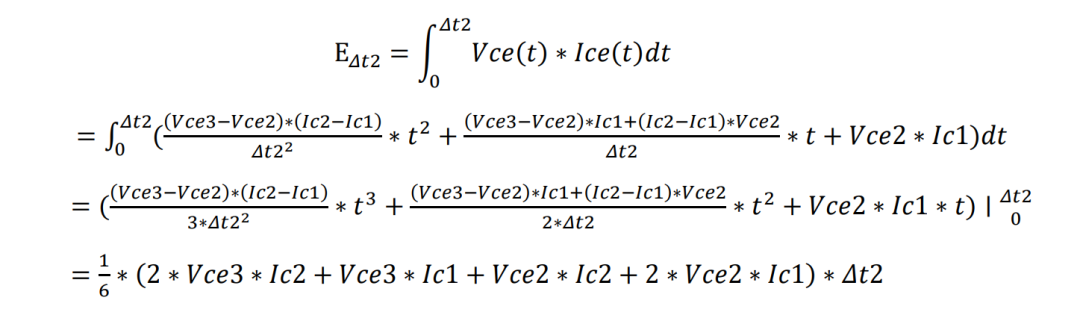
从波形中可以读出:
Vce3=50V, Vce2=220V,
Ic1=20.3A, Ic2=29.3A Δt2=40ns,带入上面公式可以得到
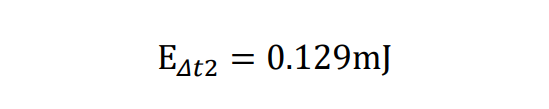
最后是Δt3部分:
四个交点:
I(0,Vce3), J(Δt3,Vce3), K(0,Ic2), L(Δt3,Ic3).
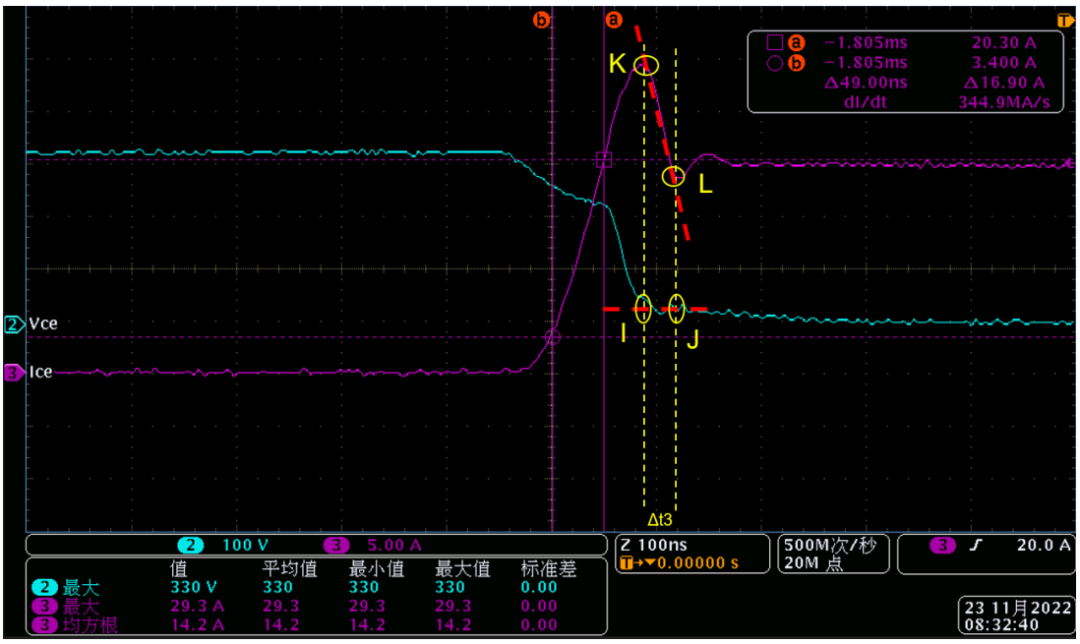
Δt3内的Vce我们取近似常数:
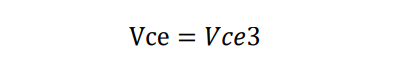
Δt3内的Ic表达式:
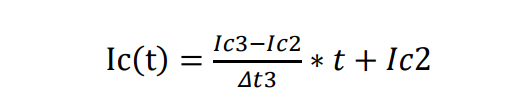
Δt3内的损耗表达式及推导:
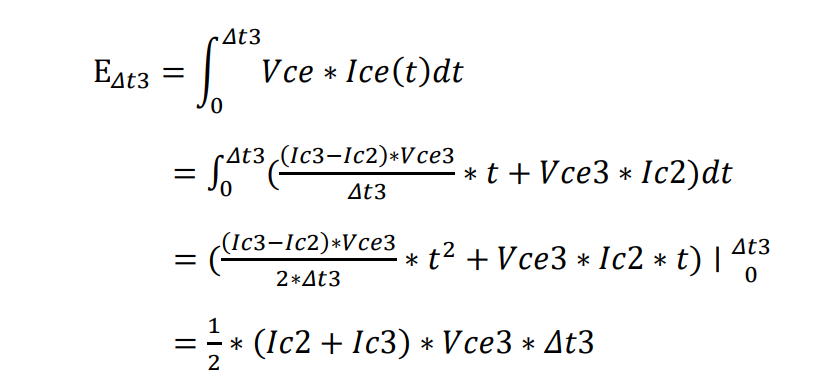
从示波器中可以读出:Vce3=40V, Ic2=29.3A, Ic3=19A Δt3=30ns, 带入上面公式可以得到
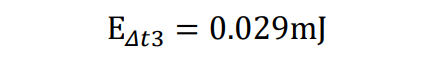
这样把三部分算好加起来就是开通的总损耗:
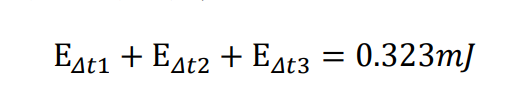
导通部分损耗计算
IGBT导通状态下处于饱和状态,我们只需要对导通状态下的饱和电压Vce和电流Ic乘积积分就可以:
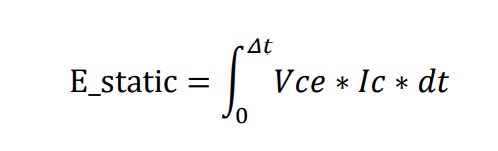
但是导通状态下的Vce实际是和Ic关联的,Vce会随着Ic的变化而变化,我们直接拿下面的实际测试波形来举例分析:
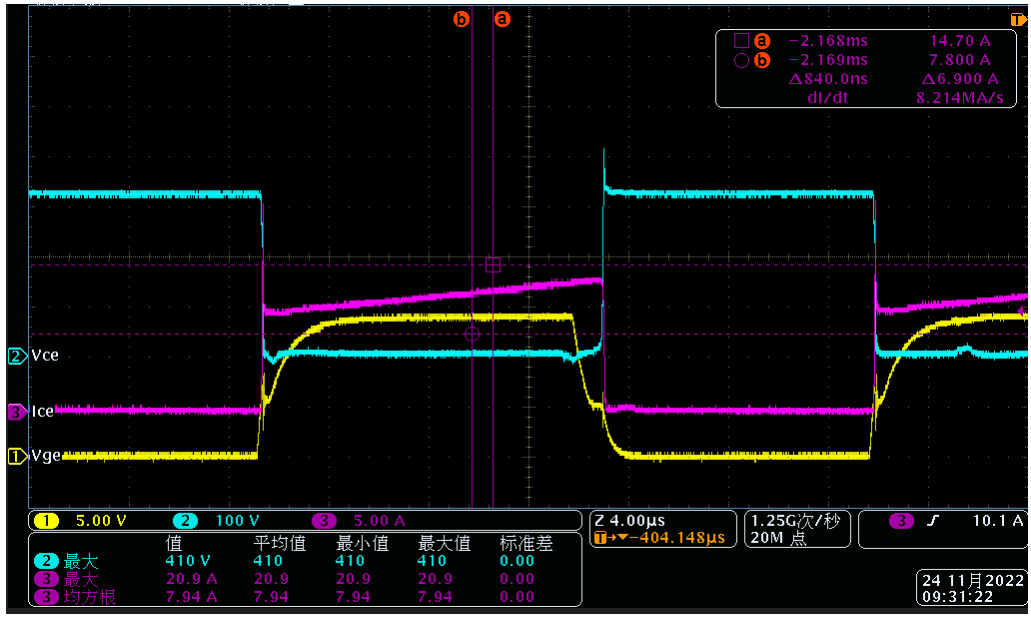
从波形上看,Ic在IGBT导通状态下是线性上升的,对应的Vce应该也是线性增加的,但是因为实际测试中Vce有高压状态的原因,我们会选择高压差分探头测试。当IGBT导通时Vce只有1-2V, 这时差分探头对低压部分的测试精度就成了问题,那么我们怎么近似的计算这部分导通损耗呢?
我们可以参考规格书中的Vce曲线:
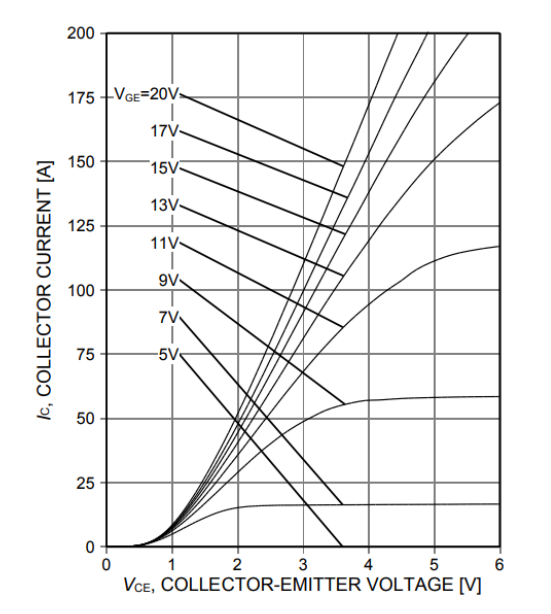
实际测试波形电流在20A左右,所以我们把20A左右的曲线单独放大取出来:
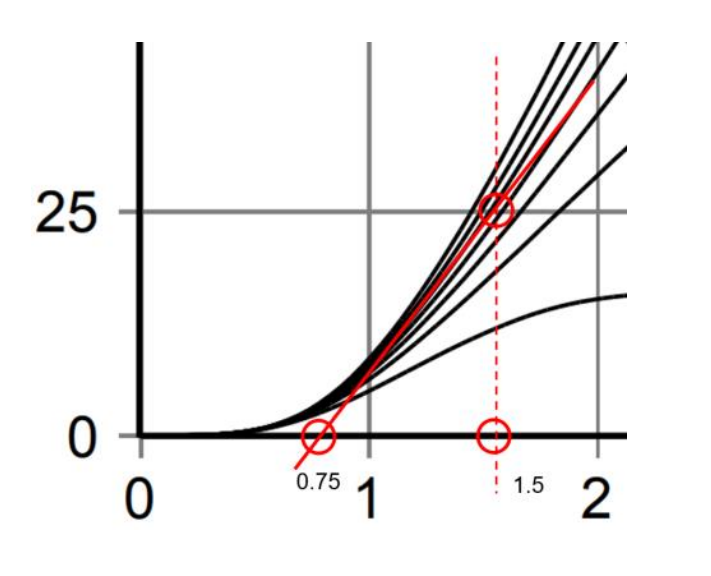
Vce表达式:
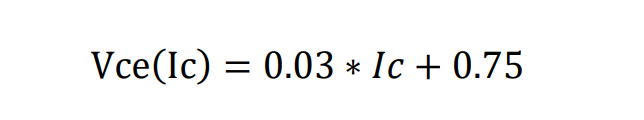
然后我们来看电流部分,首先我们在波形上取A,B两点,导通时间Δt,如下:
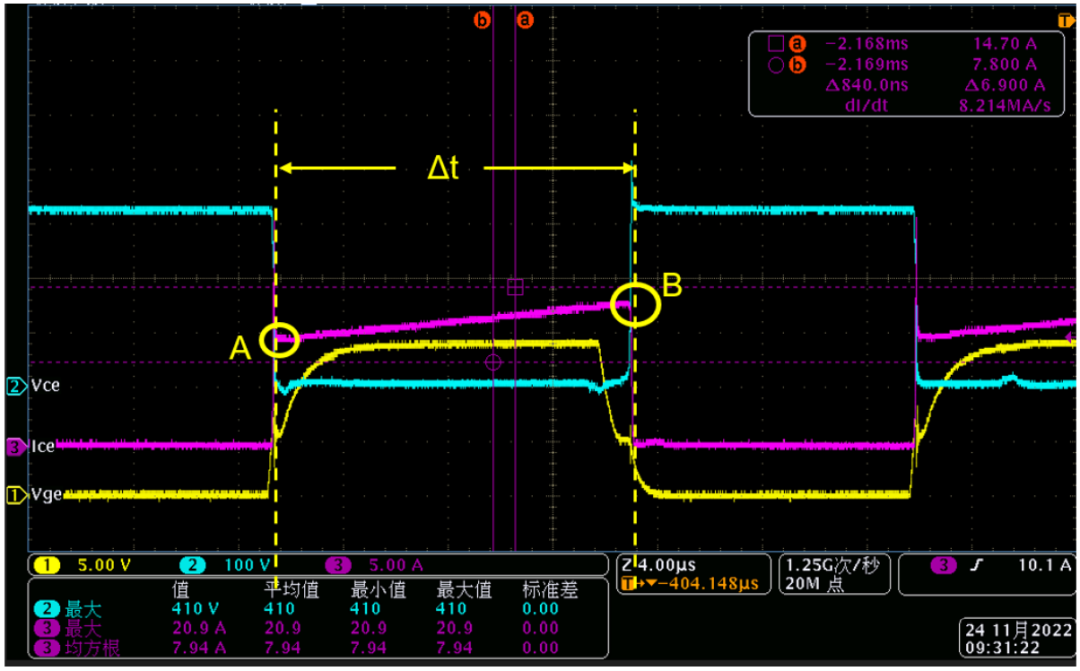
两个点坐标:A(0,Ic1), B(Δt,Ic2):
Δt内的Ic表达式:
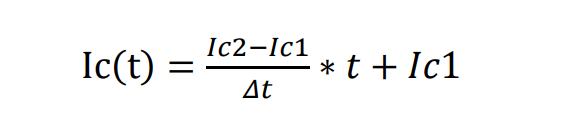
Δt内的导通损耗表达式及推导:
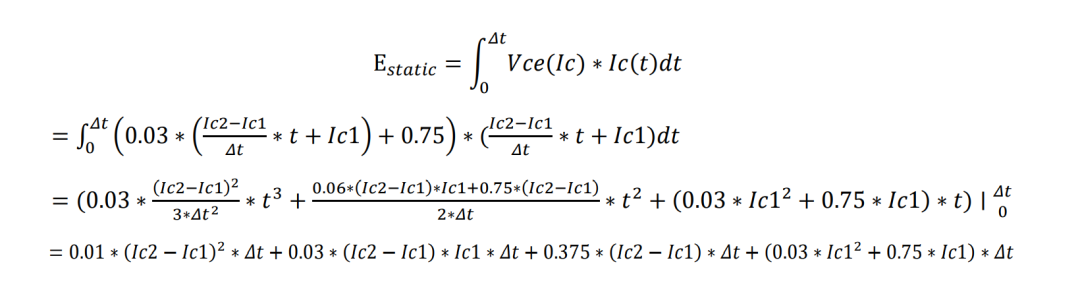
从波形中可以读出:Ic1=9.5A, Ic2=14A, Δt=14us,带入上面公式可以得到
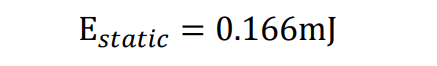
注:关于Vce-Ic曲线,规格书中通常会提供常温(25度)和高温(150度或者175度)两种,为了贴近实际工作状态,建议选择高温曲线。
开关损耗-关断部分
先看理想的IGBT关断波形:
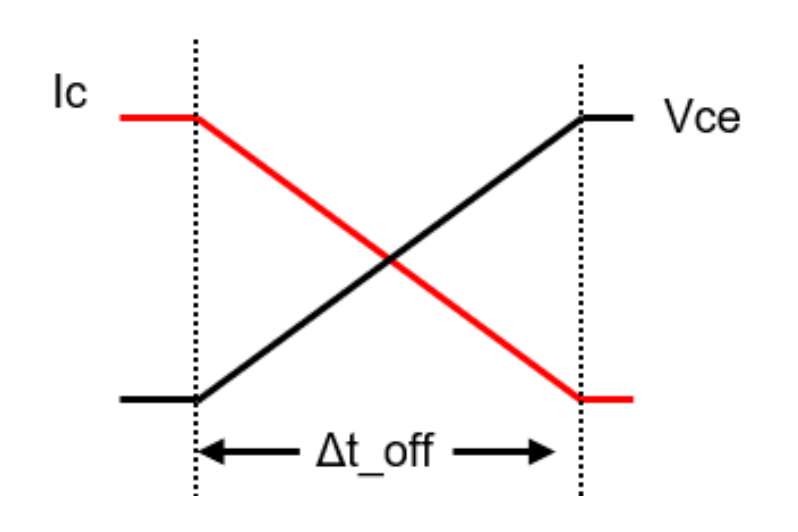
电流线性方程,分别找到电流开关波形中的两个坐标(0,Ic) 和 (Δt_off, 0) , 那么电流线性方程:
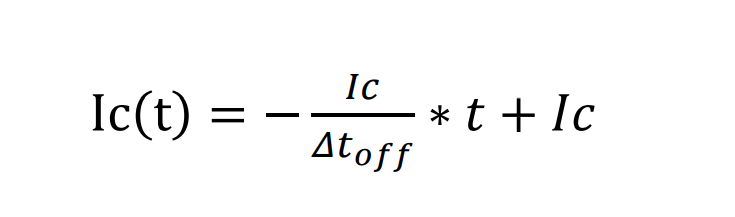
电压线性方程,同样找到电压波形中的两个坐标(0,0), (Δt_off,Vce), 那么电压线性方程:
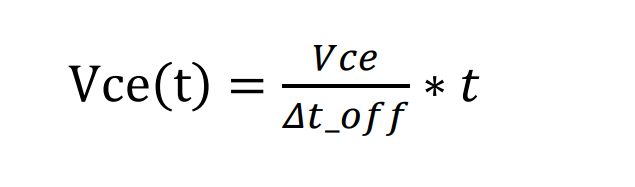
根据损耗计算的定义:
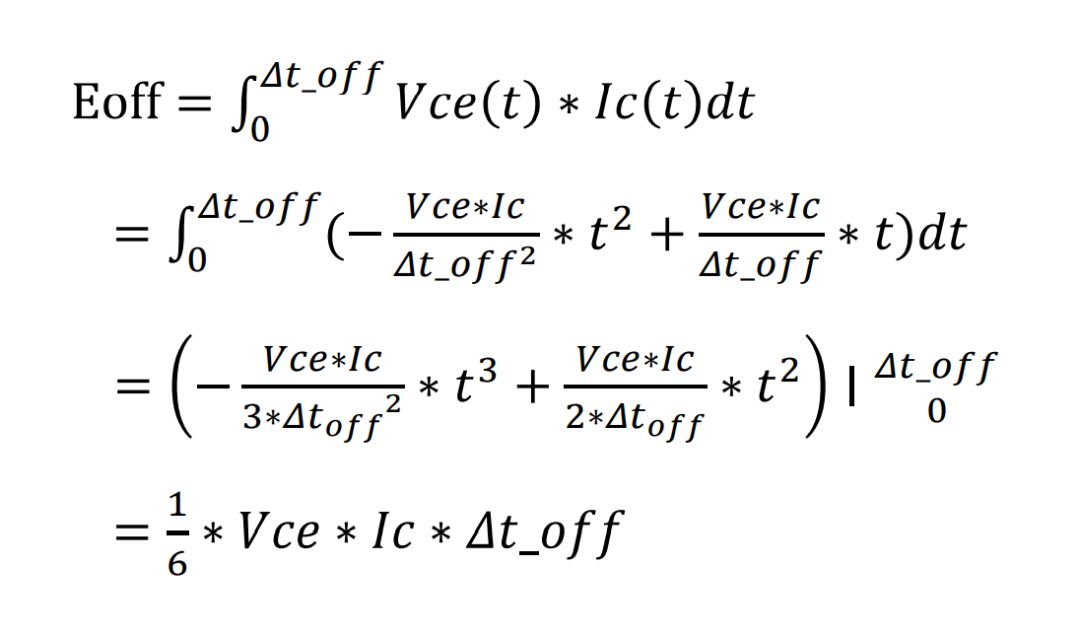
实际的关断波形:
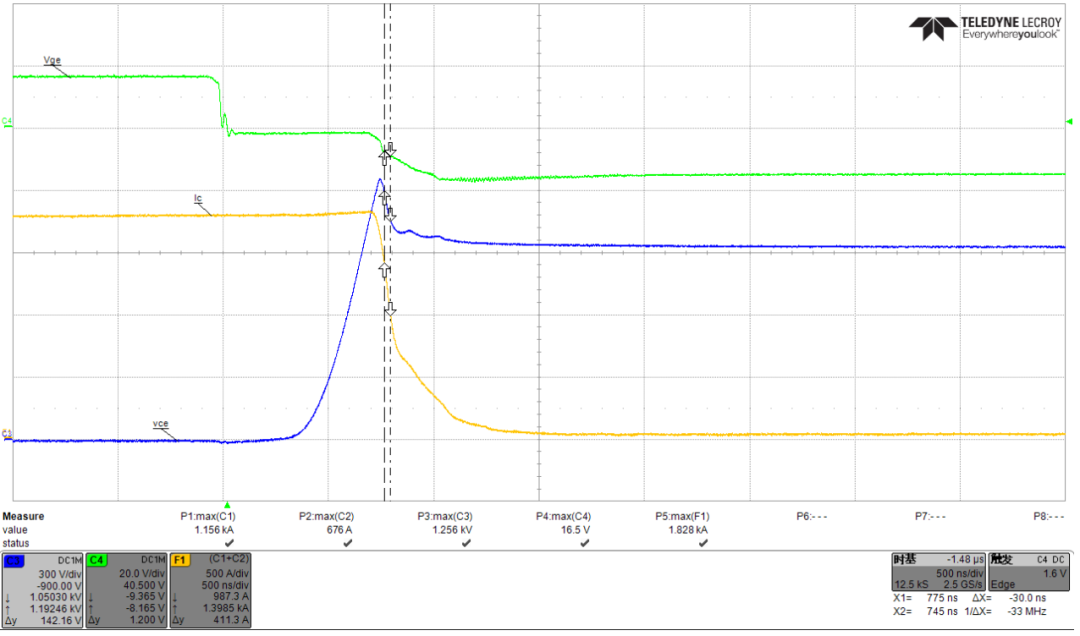
基于上面实际关断波形的损耗计算,想给大家留个作业,计算方法可以参考开通损耗部分的计算推导过程,感兴趣的小伙伴可以试一下。
这样损耗的计算方法介绍完了,我们对于基础高等数学知识的复习也告一段落。
来源:邱玉强,田斌










