技术咨询
代买器件
商务客服
研发客服前两期介绍了Clarke的Park变化的基本原理，但是经过这两种变换后会存在两种系数，相信大家都很迷惑，这是什么原因? 主要原因是存在两种遵循的方式：1、变换前后电流所产生的旋转磁场等效且电机输出功率不变; 2、变换前后电流所合成的空间矢量等效且电机输出功率不变。 这两种最后方式是造成系数不同的根本原因，实际应用中可以根据需要选择相应的变换等效原则。
这一期设计的理论计算能力比较强，强烈建议观看的小伙伴找个安静的角落，哪张纸和笔进行计算!
01依据旋转磁场等效变换
遵循的两个原则：
a、变换前后电流所产生的旋转磁场等效;
b、变换前后两系统的电机输出功率不变;
1.1、Clarke变换
图1-1是ABC和αβ两个坐标系，取α轴与A轴重合，并假定三相绕组每相有效线圈匝数为N3，两相绕组每相有效线圈匝数为N2，两种坐标系中每相的磁动势均为有效线圈匝数与该相电流的乘积。
图1-1 Clarke坐标变换矢量示意图1
由图1-1得出磁势守恒式子为：
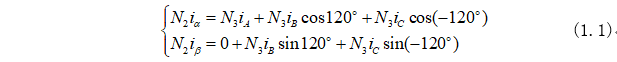
由式(1.1)变形化为矩阵形式为：
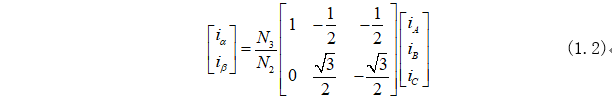
为了方便分析，引入零轴变量为：
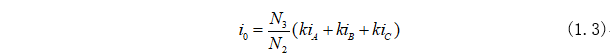
将式(1.3)合并到式(1.2)可以得到αβ0轴坐标系方程为：
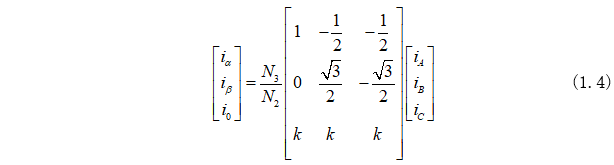
这里定义Clarke矩阵为：
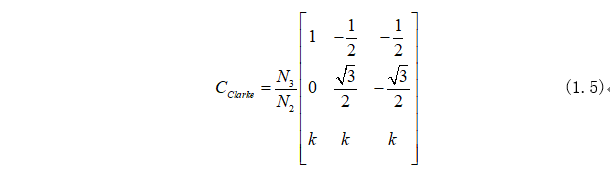
坐标变换中需要确保电机输出功率不能发生变化，故功率计算表达式为：
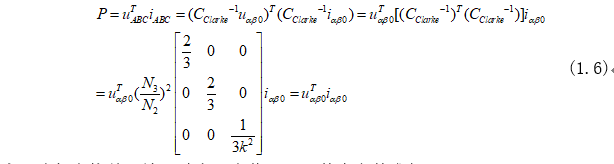
为了确保变换前后输出功率不变化，可以其中参数求得：
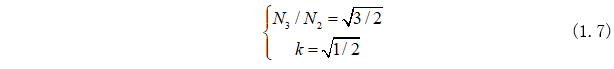
因此Clarke变换式为：
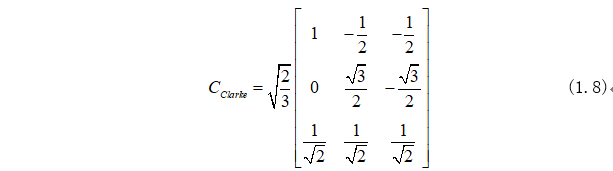
1.2、Park变换
图1-2是两相旋转坐标系转速w随着电机转子转动，αβ是两相静止坐标系，dq是两相旋转坐标系。
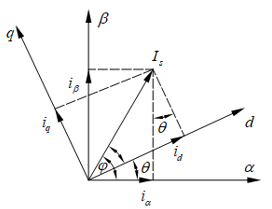
图1-2 Park坐标变换示意图1
由第二期内容可知，Park变换式为：
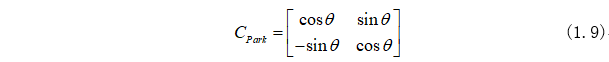
1.3、功率计算
电机功率可以计算为：
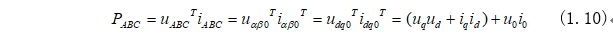
02依据空间矢量等效变换
遵循的两个原则：
a、变换前后电流所合成的空间矢量等效;
b、变换前后两系统的电机输出功率不变;
2.1、Clarke变换
图2-1中空间矢量Is在αβ轴上的投影分别为ia、iβ，且与A轴夹角为φ。
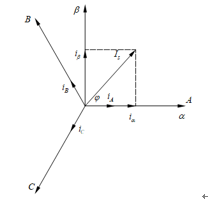
图2-1 Clarke坐标变换矢量示意图2
根据图2-1所示可以得到三相电流与空间矢量Is关系式为：
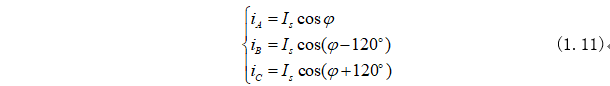
同理可以得到两相静止坐标系中电流ia、iβ与空间矢量Is关系式为：
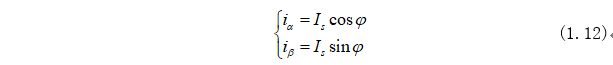
根据三角恒等式：
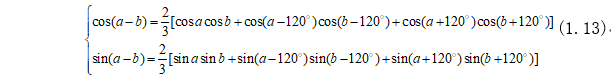
根据三角恒等式(1.13)将式(1.12)变化为：
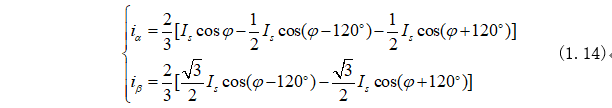
写成矩阵形式为：
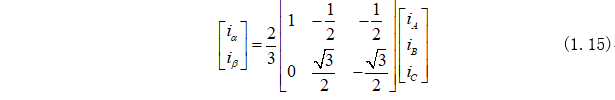
同样，引入零轴变量：
将式(1.16)代入式(1.15)中可以得到新的矩阵形式为：
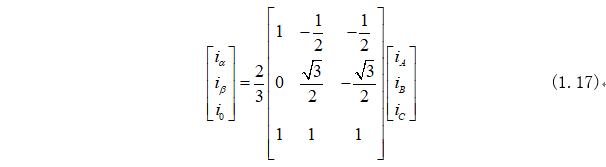
那么Clarke变换矩阵为：
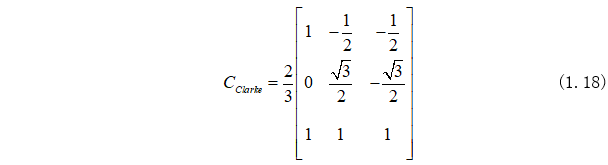
2.2、Park变换
同样，图2-2是两相旋转坐标系转速w随着电机转子转动，αβ是两相静止坐标系，dq是两相旋转坐标系。
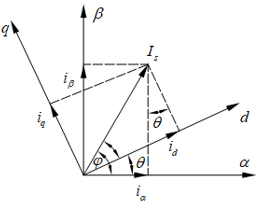
图2-2 Park坐标变换示意图2
由第二期内容可知，Park变换式为：
2.3、功率计算
电机功率可以计算为：
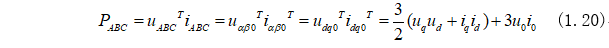
03总结
由磁动势守恒计算出的电机功率为：
由空间矢量守恒计算出的电机功率为：
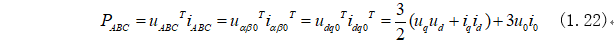
两种变换存在一个3/2的系数区别，主要是各自采用了不同的变换形式，最后得出的功率都是对的!
相关文章
