1.概述：

应用矢量控制时其坐标变换是基础，相关文献与资料都有很多，matlab还有自带模块，但是一般都直接就给个变换矩阵让人晦涩难懂。本文分享学习理解与推导过程。

2.Clarke变换分析推导过程

引用空间概念可得：

根据分析建模：

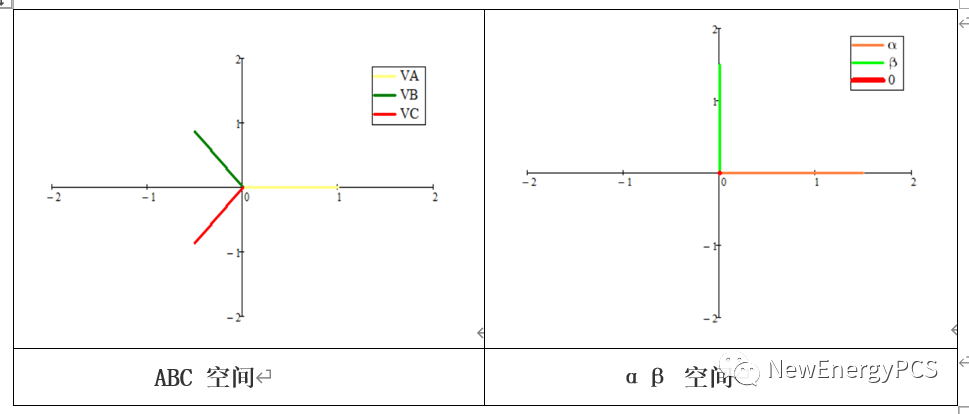
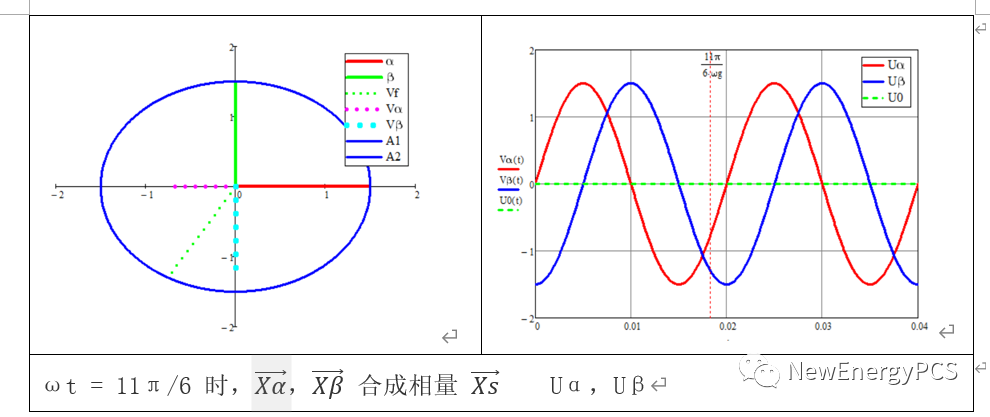
可得结论：

abc 系统转换为αβ系统的变换就是Clarke变换。在上面的分析中旋转矢量的长度相等，得到Uα，Uβ的幅值是3/2，通过调整Clarke变换中的系数，可以调整abc 系统与αβ系统中的幅值大小相等，功率相等，有效值相等。被称为恒幅值变换，恒功率变换，恒有效值变换。

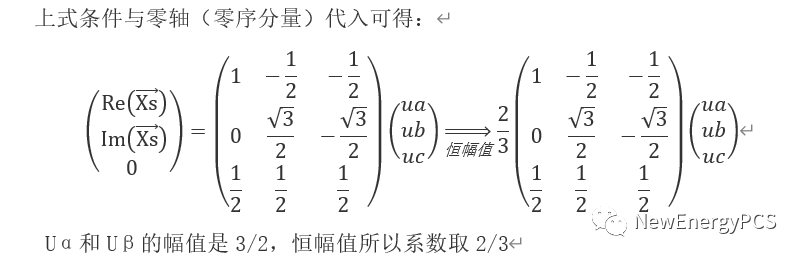
通过上式使用mathcad搭建ABC三相静止坐标与αβ 0两相静止坐标。三相对称时零轴分量为0 。

注意上图使用sin正弦量用正序A B C作 3S/2S变换，发现波形上Uα超前Uβ 90°。与我们定义的αβ 0两相静止坐标，β轴超前α 90°相反。这里有两种方法修改模型，其一是我们修改sin正弦量把原来的正序改为负序A C B。

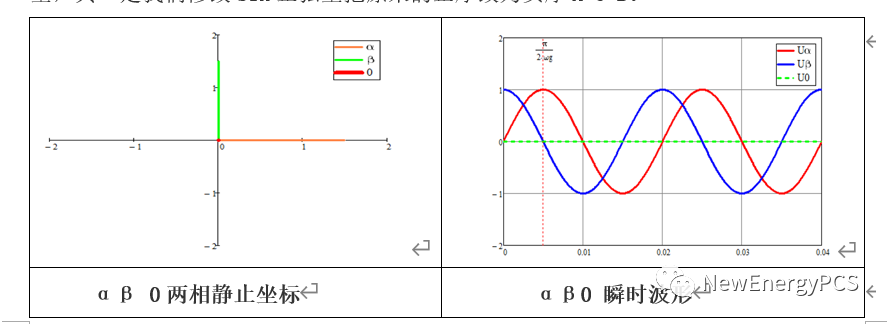
通过修改相序后需要修改clarke变换矩阵第二行的元素反号，即更改为了习惯的逆时针旋转。

在这里声明参考MATLAB官网的参考文档，就暂时不修改相序，但也默认β轴超前α90°，使用mathcad可得如下波形图矢量图。

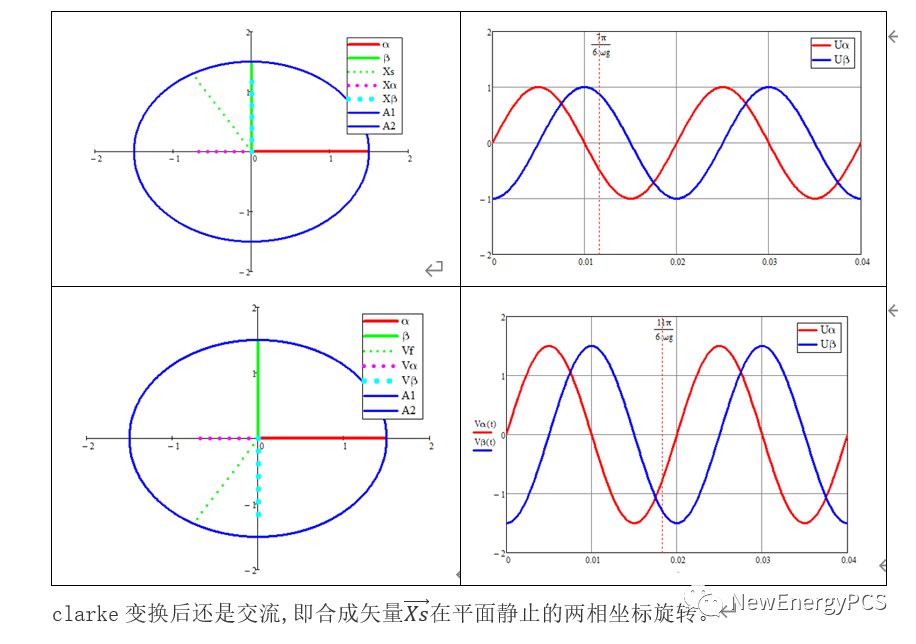
3.park变换分析推导过程

如果将原本平面静止的两相坐标以同平面旋转矢量相同的角速度旋转起来与其相对静止，这时原来的旋转矢量可以看做是相对于坐标静止的直流分量。称这两分量为d，q分量。并且定义q轴超前d轴90°。2s/2r park变换既然是旋转变换，就存在对齐问题与旋转方向问题。那么就有α轴对齐d轴称为d轴定向，或者α轴对齐q称为q轴定向。

d轴定向mathcad仿真如下：

通过用d轴定向park变换矩得到了直流分量，但q轴分量为负，（从d轴定向的矢量图看，q轴应该为正，应为q轴超前d轴90）。产生这个结果的原因是在clarke变换时，默认了β轴超前α90°。而实际上clarke变换时β轴滞后α 90°。

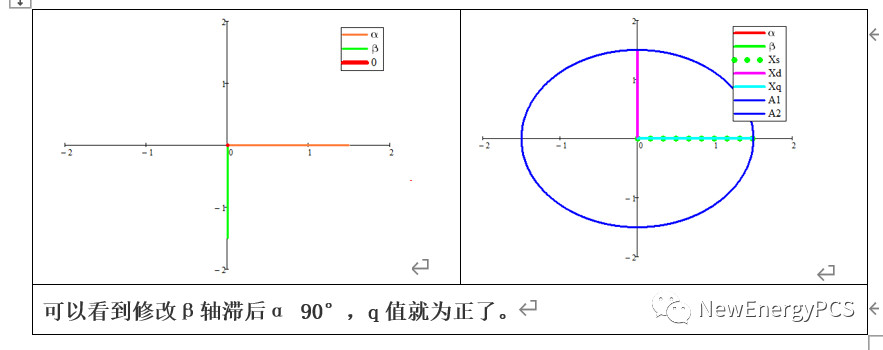
q轴定向mathcad仿真如下：

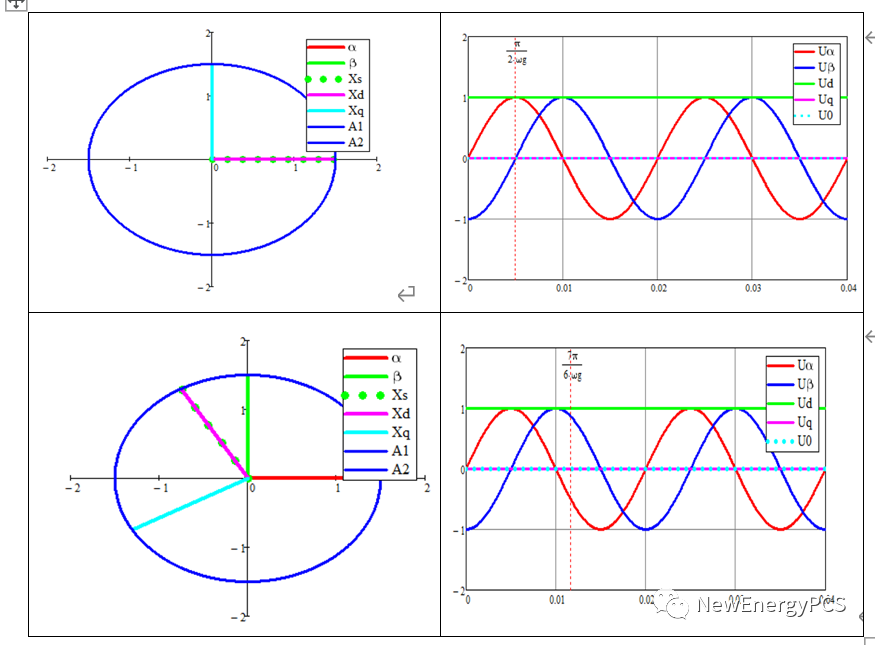
结论1：

使用不同的定义会有不同的clarke park变换矩阵，就需要做些匹配：如Clarke变换中正序改负序，锁相环（PLL）输出相角与park矩阵中的θ匹配。即PLL输出角度作为park矩阵的θ角度时需要偏移90°。那么就要判断三相系统为“正弦形式”或“余弦形式”，观察系统三相波形与PLL输出相位特征来判断。

上图为物理中描述物体简谐运动的旋转矢量法示意图。当旋转矢量的初始位置为图中A点时，矢量旋转一周其值将经历ABCD的大小变化；当旋转矢量位置为图中D点时，，矢量旋转一周其值将经历DABC的大小变化；此处称A点初始位置为余弦形式，D点为初始位置时为正弦形式。

结论2：

三相系统（abc坐标系）的时域分量转换为正交静止坐标系（αβ）中的两个分量。被称为3S/2S，（三相静止坐标转换为二相静止坐标）即clarke变换。将αβ坐标系中的两个分量转换为一个正交旋转坐标系（dq）。也被称为2s/2r，（二相静止坐标转换为二相旋转坐标系）即park变换。连续实现这个两个变换可将交流电流和电压转换为直流信号从而简化计算，主要原因还是常用的控制器是经典的PI调节器，PI调节器可以对直流量进行无净差调节，而交流量不行，所以将三相交流分量转化为两项直流分量做控制。

3.Clarke park逆变换分析推导过程：

由于PI控制器输出是直流量， 那么就产生了上述相反的变换需求，即反park变换2r/2s，反park变换2S/3S。连续实现这个两个变换可将直流电流和电压转换为交流信号，再将交流信号提供给PWM模块作为参考信号进而控制。