1.半桥逆变框图：

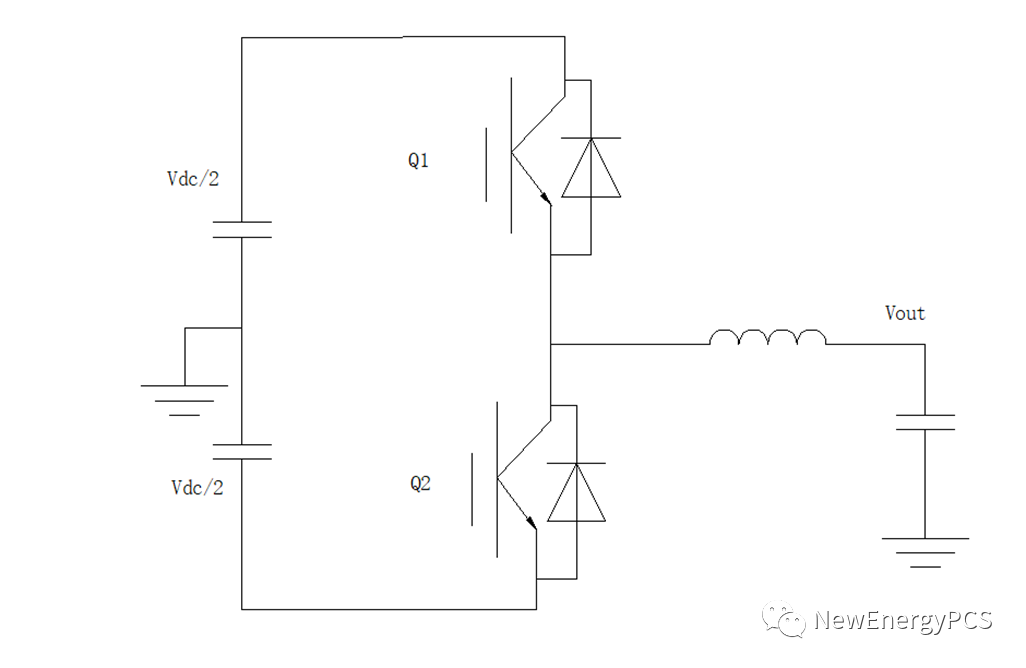
1.输出平均值推导：

逻辑关系：两管同时导通短路，所以不能两管同时导通

Q1导通，Q2关闭 Vout=1/2Vdc，Q2导通，Q1关闭 Vout=-1/2Vdc可得：

2.载波最大值推导：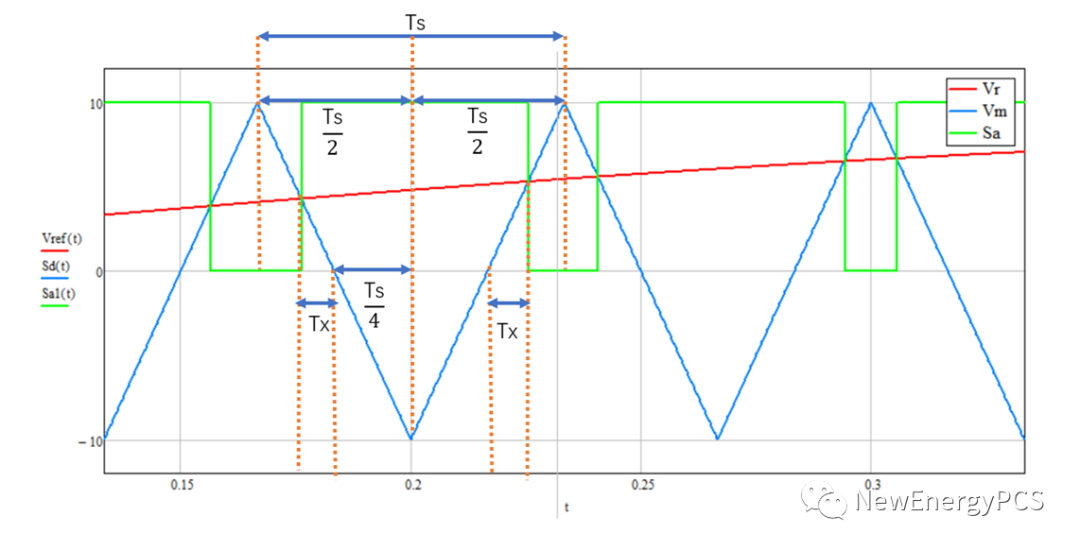

3.占空比分析推导：

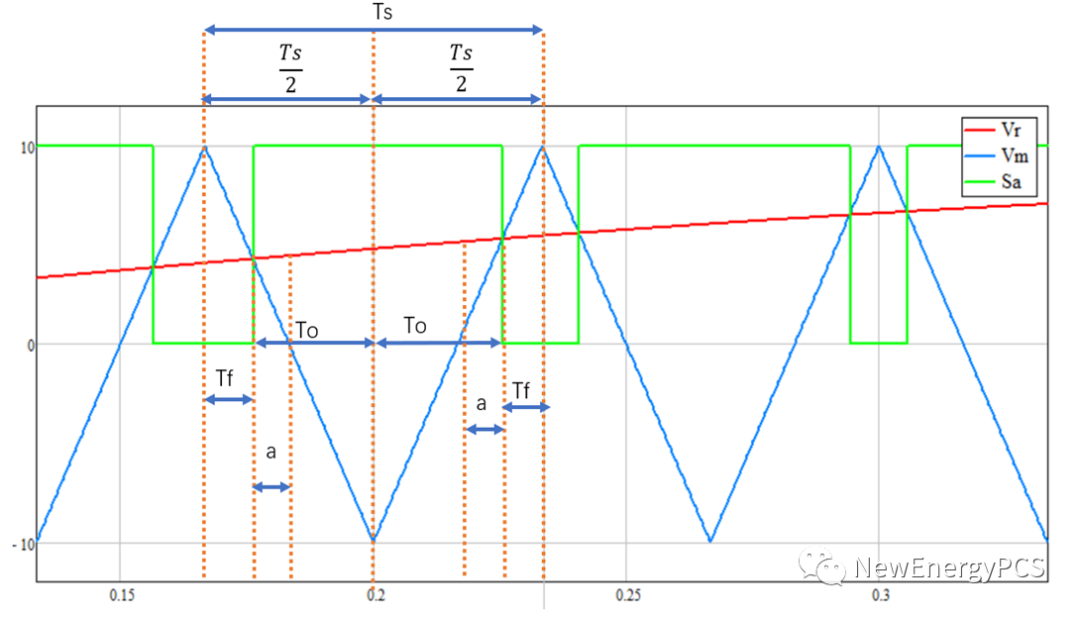相似三角形可得：

4.谐波分析推导：

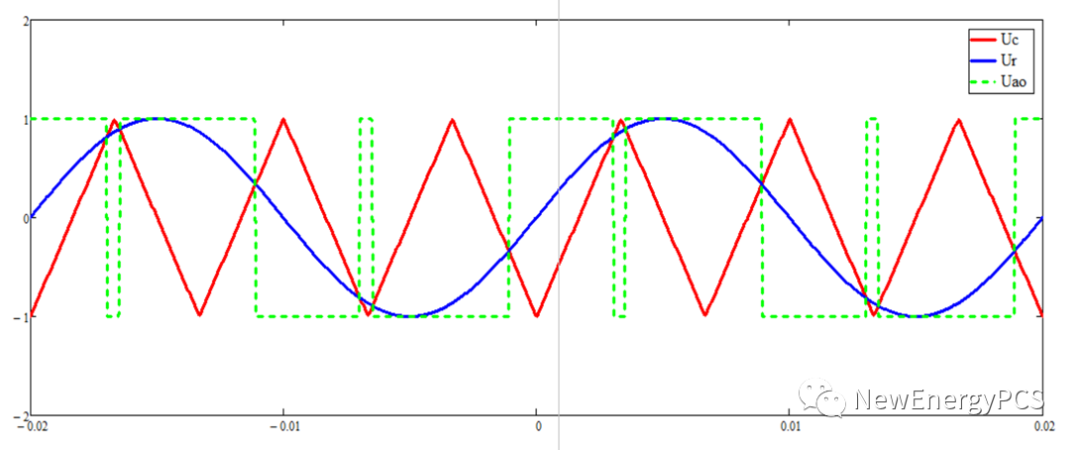
单相双极性工作方式的调制波Ur，载波Uc，输出电压波形Uao：

调制波函数：Ur=Vmsin(ωt+φ)

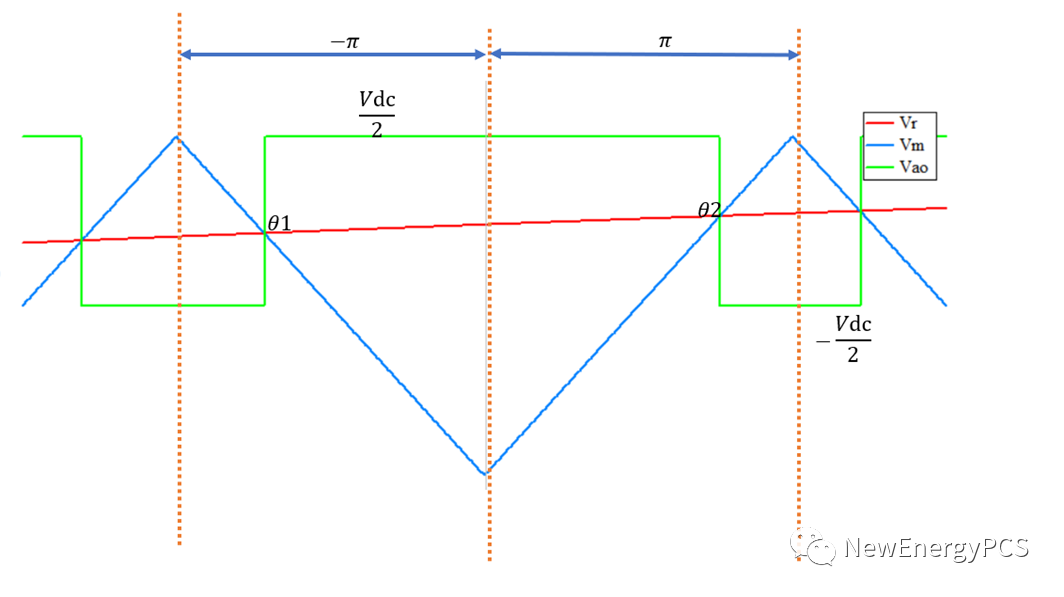
载波频率为基准的傅里叶分析方式，取一个载波周期分析输出电压可得：

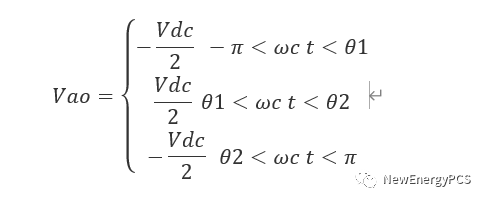
根据傅里叶公式展开Vao得到：

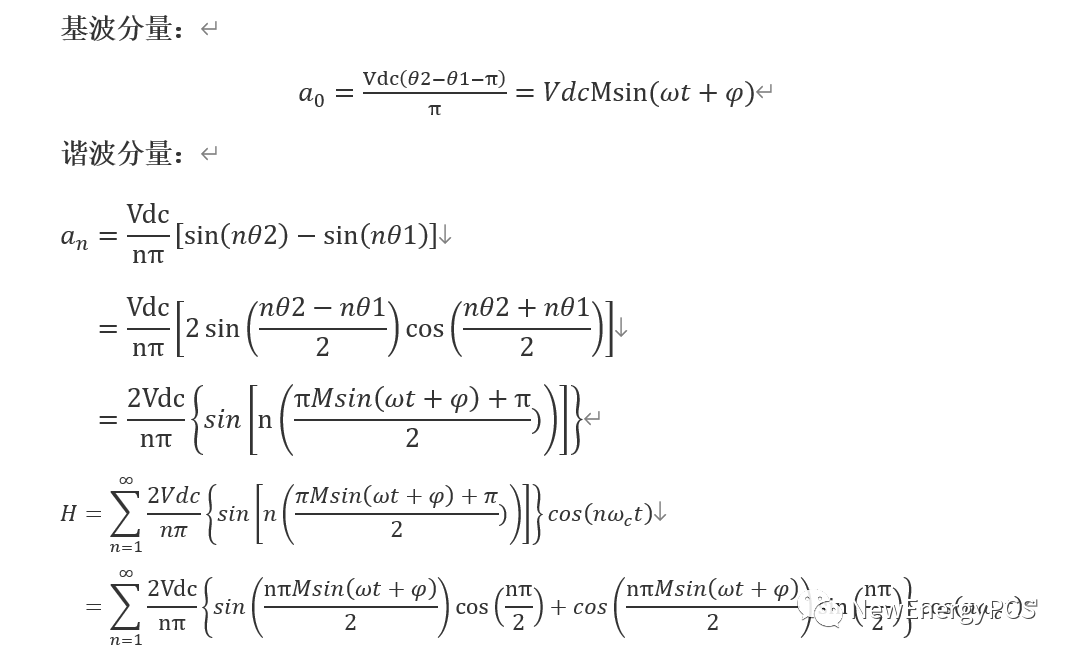
贝塞尔公式：

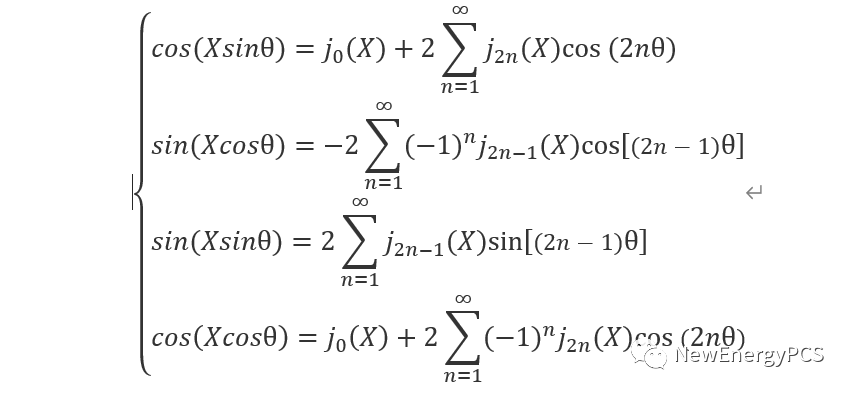
代入谐波公式：

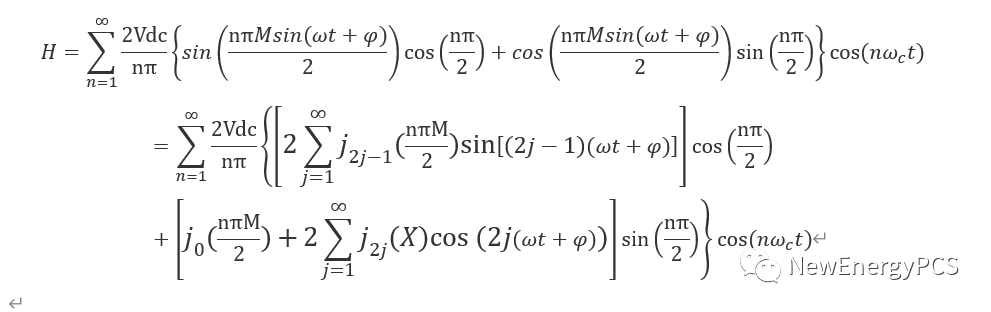
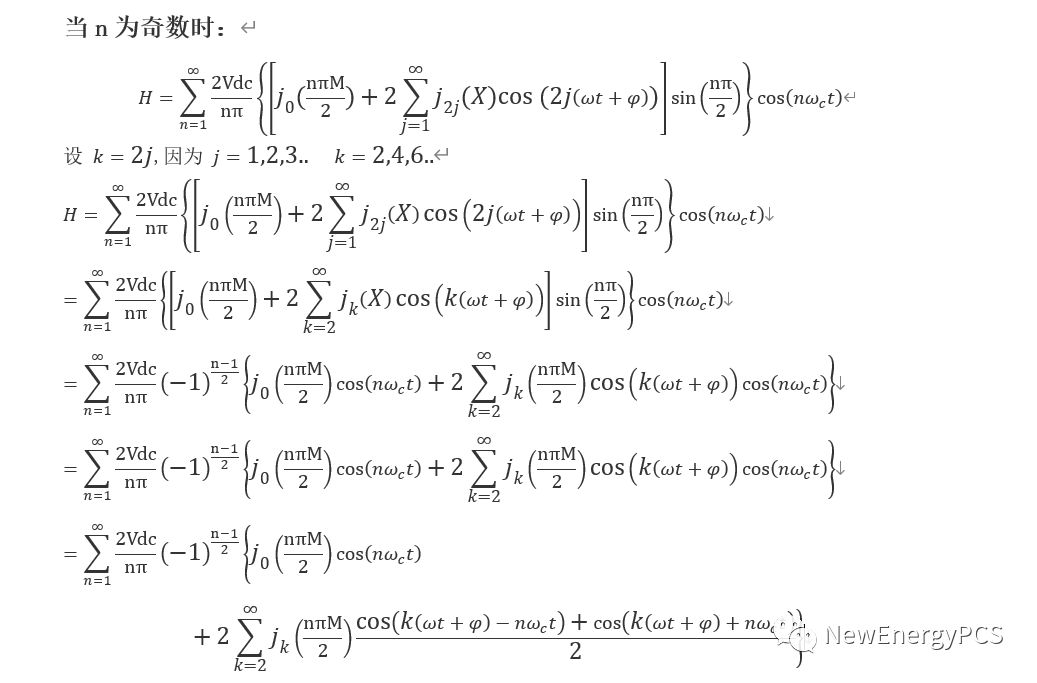
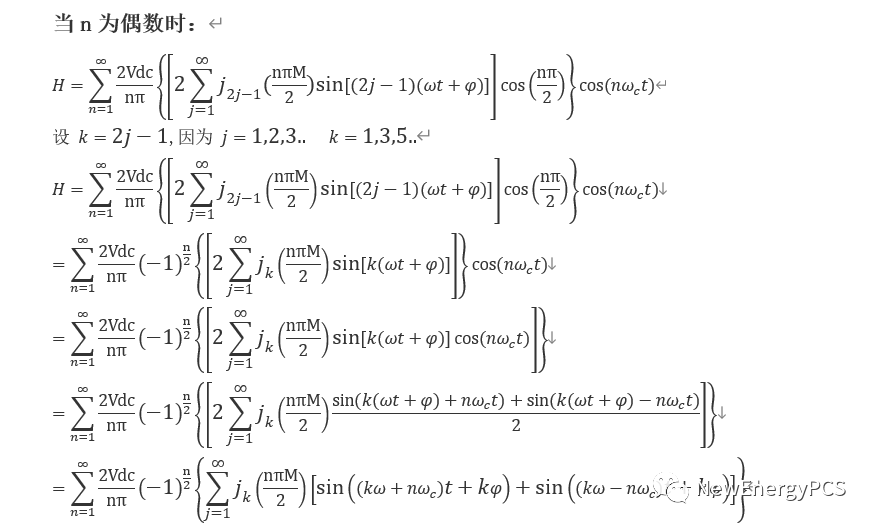
mathcad建立辅组Γ函数用于求解n阶贝塞尔函数，也被称为第一类Bessel函数。贝塞尔函数是贝塞尔方程的解，它们和其他函数组合成柱调和函数。除初等函数外，在物理和工程中是最常用的函数。

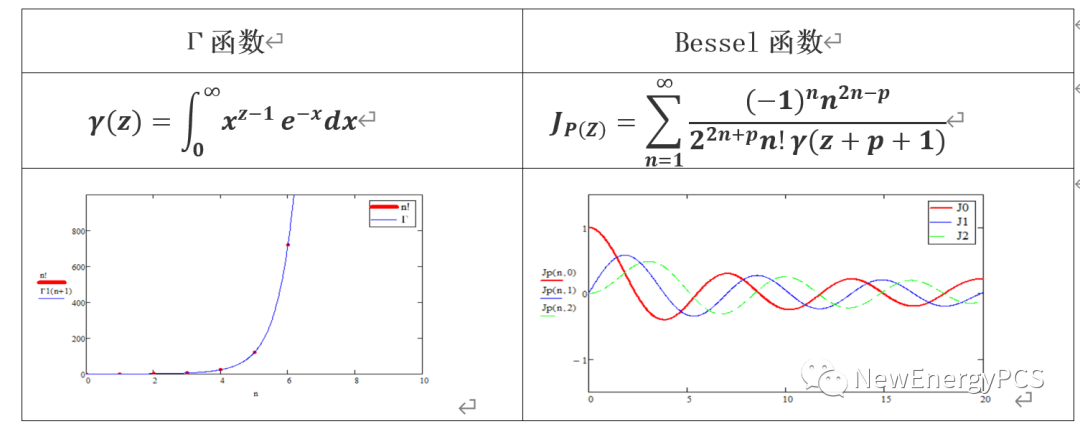
根据贝塞尔函可得谐波分布情况：

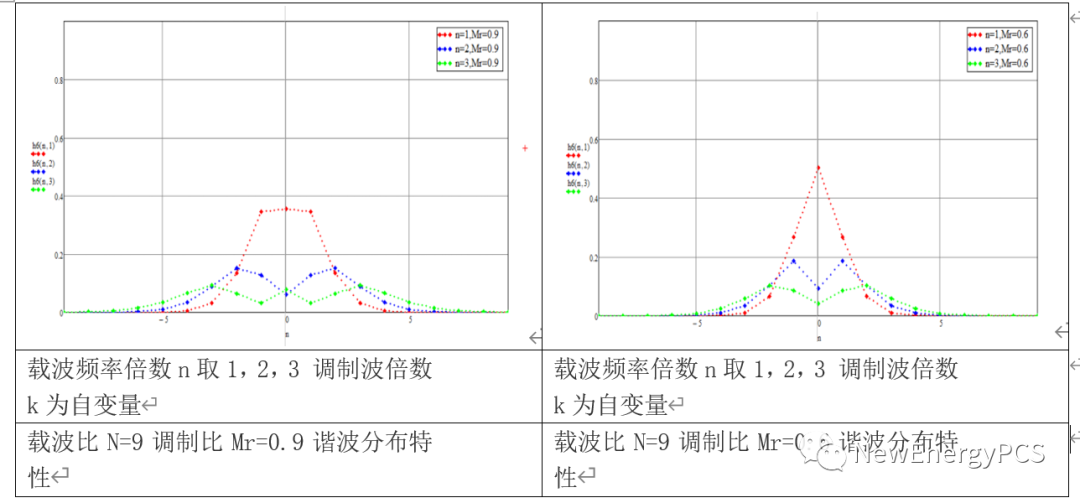
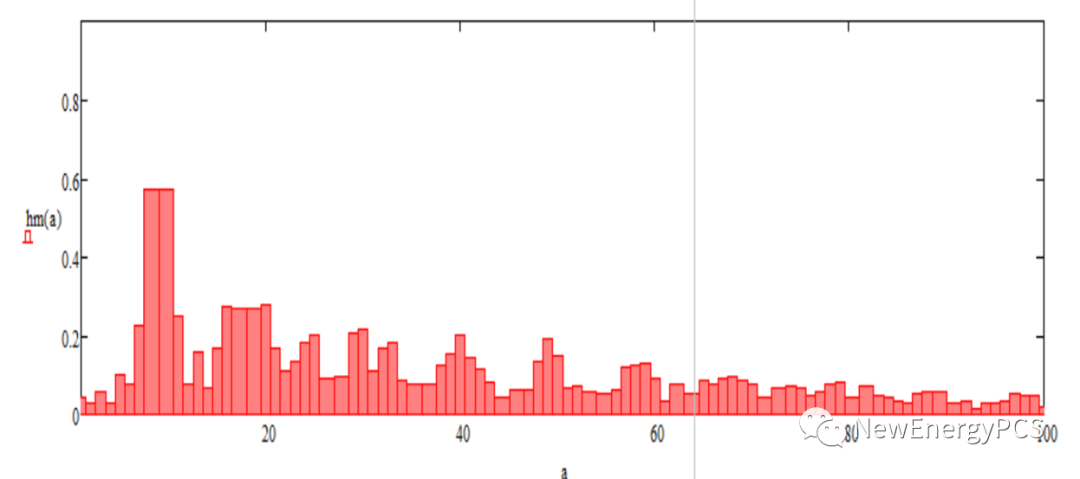
载波频率（开关频率）处及其附近的谐波（n=0,±2等），是主要谐波，计滤波器时主要考虑这些谐波。在所有谐波中，幅值最大的谐波出现在开关频率（n=1,k=0）处。2倍及以上倍开关频率附近的边带谐波幅值较低。频谱的分布不只与Mr的大小有关，也与载波比N有关；Mr可以改变谐波的幅值，而N可以改变谐波的频率。N越大，谐波频率越高，滤波越容易。当N达到一定值时，只用几个微法的电容就可以达到比较好的滤波效果（可以将设备做的比较小），这就是提高开关频率的主要原因。

结论：

桥臂开关谐波分量的解析法比较复杂，用双重傅里叶级数分解为调制波角频率倍数的谐波，而采用以载波的角频率为基准，考察边频带谐波分布情况的方法是比较常见的。