无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确与稳定

什么是相机标定？

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。

在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定。

计算机视觉的基本任务之一是依据相机获取的图像信息计算三维空间中物体的几何信息，并由此重建和识别物体。我们用简单的数学模型来表达复杂的成像过程，并且求出成像的反过程。标定之后的双目相机，可以进行三维场景的重建，这是计算机视觉的一大分支。

经典的针孔相机模型

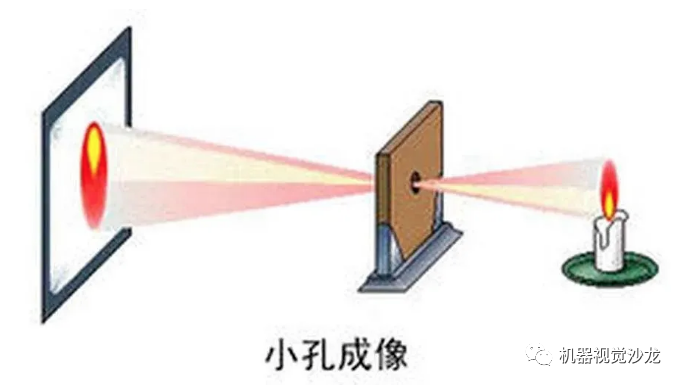
小孔成像的实验大家都很熟悉，如上图，依据这个实验也可以抽象出一个经典的针孔相机模型，如下图：

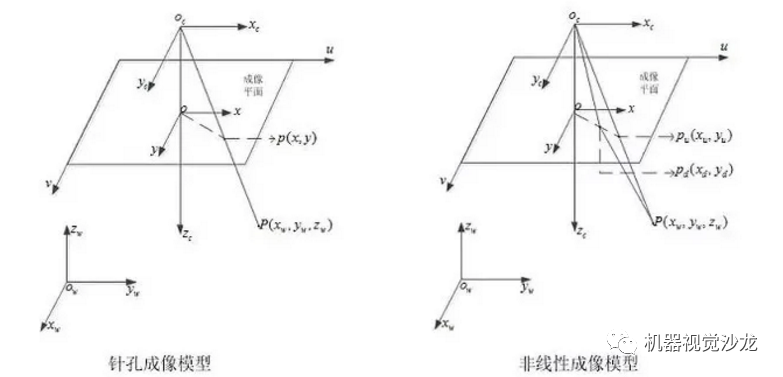
相机标定常用到四种坐标系，分别为：

1）像素坐标系（u，v）：描述物体成像后的像点在数字图像上（相片）的坐标，单位为个（像素数目）。

2）成像平面坐标系（x，y）：描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系，单位为m。

3）相机坐标系（xc，yc,  zc）：原点落在相机上的三维坐标系，单位为m。

4）世界坐标系（xw，yw,  zw）：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入，单位为m。

世界坐标系到相机坐标系的转换关系今天暂不讨论，我们把重点放在相机坐标系到成像平面坐标系的转换关系上。

上文中小孔成像实验的成像过程可以描述为一点通过针孔相机模型的示意图（如图A）。为了在数学上更方便描述，我们将相机坐标系和图像坐标系位置对调，变成图B所示的布置方式：

图A

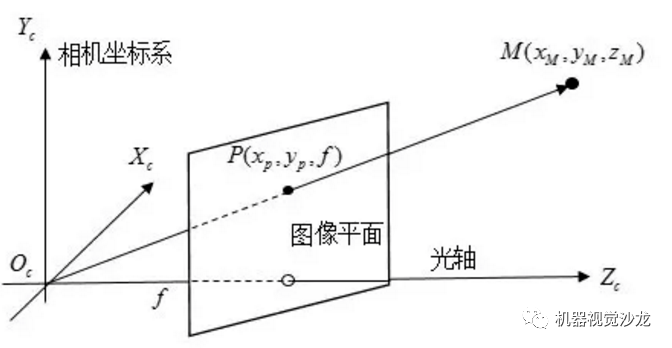
图B

经过一系列推导，我们就可以得到一个结果转化公式：

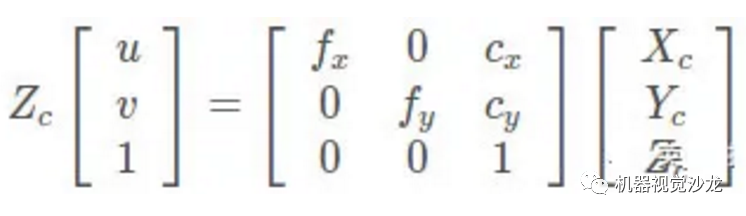
透镜的畸变

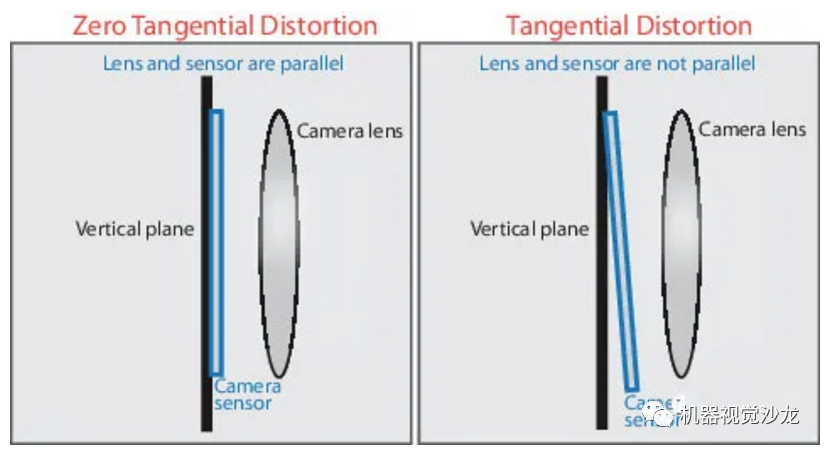
透镜的畸变主要分为径向畸变和切向畸变：

径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图。

切向畸变是由于透镜本身与图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。

常用的相机标定方法

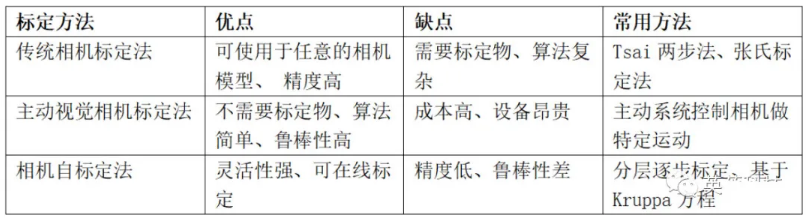
常用的相机标定方法有：传统相机标定法、主动视觉相机标定方法、相机自标定法。

1）传统相机标定法

传统相机标定法需要使用尺寸已知的标定物，通过建立标定物上坐标已知的点与其图像点之间的对应，利用一定的算法获得相机模型的内外参数。根据标定物的不同可分为三维标定物和平面型标定物。传统相机标定法在标定过程中始终需要标定物，且标定物的制作精度会影响标定结果。

2）主动视觉相机标定法

基于主动视觉的相机标定法是指已知相机的某些运动信息对相机进行标定。该方法不需要标定物，但需要控制相机做某些特殊运动，利用这种运动的特殊性可以计算出相机内部参数。基于主动视觉的相机标定法的优点是算法简单，往往能够获得线性解，故鲁棒性较高，缺点是系统的成本高、实验设备昂贵、实验条件要求高，而且不适合于运动参数未知或无法控制的场合。

3）相机自标定法

相机自标定算法主要是利用场景中的一些平行或者正交的信息。其中空间平行线在相机图像平面上的交点被称为消失点，它是射影几何中一个非常重要的特征，所以很多学者研究了基于消失点的相机自标定方法。自标定方法灵活性强，可对相机进行在线定标。但由于它是基于绝对二次曲线或曲面的方法，其算法鲁棒性差。

视觉镜头基础知识

为什么需要镜头？

肉眼结构：

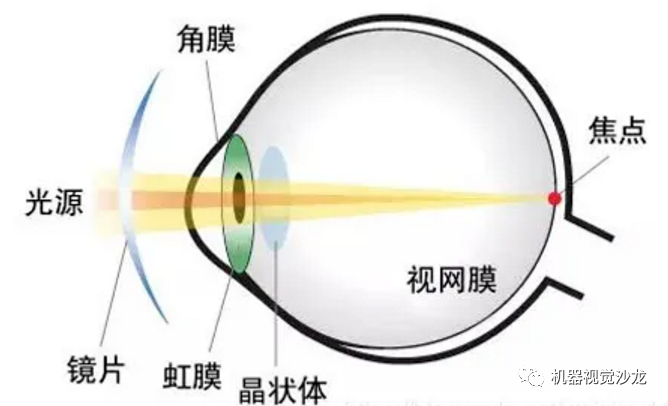
镜头相当于充当晶状体这一环节，简而言之，镜头主要的作用就是聚光。为什么要聚光？比如说在大晴天用放大镜生火，你会发现阳光透过放大镜聚集到一点上，也就是说，想通过一块小面积的芯片去承载这么一片区域就不得不使用镜头聚焦。

镜头内部结构

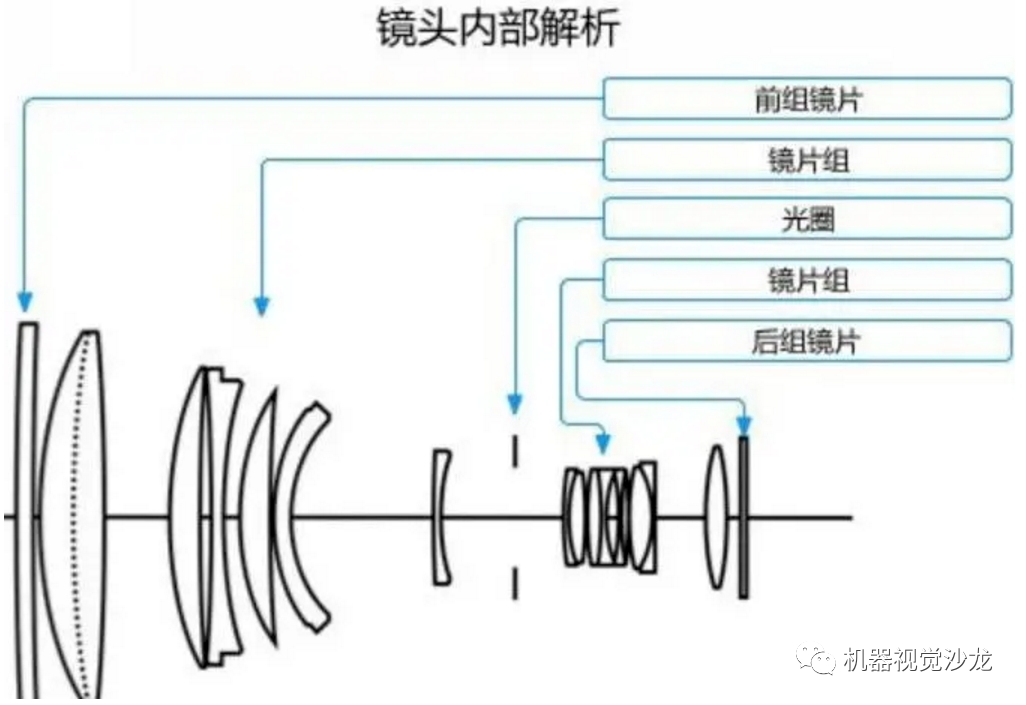
焦距

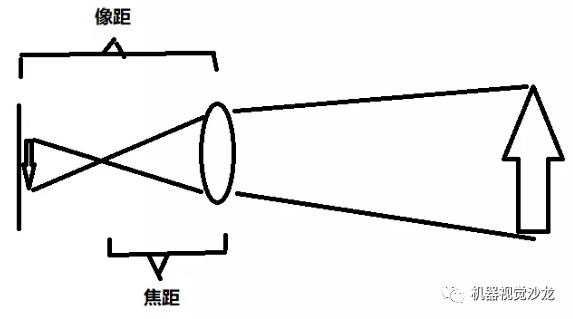
焦距是从镜头的中心点到胶平面上所形成的清晰影像之间的距离。焦距的大小决定着视角的大小， 焦距数值小，视角大，所观察的范围也大；焦距数值大，视角小，观察范围小。根据焦距能否调节，可分为定焦镜头和变焦镜头两大类。

成像的条件：焦距 < 像距 < 2倍 焦距

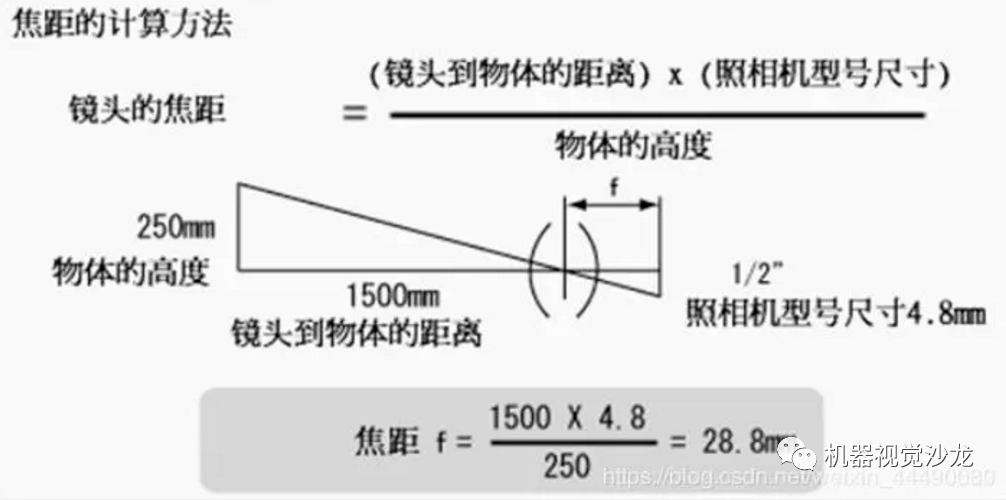
光圈

光圈是一个用来控制光线透过镜头，进入机身内感光面光量的装置，它通常是在镜头内。

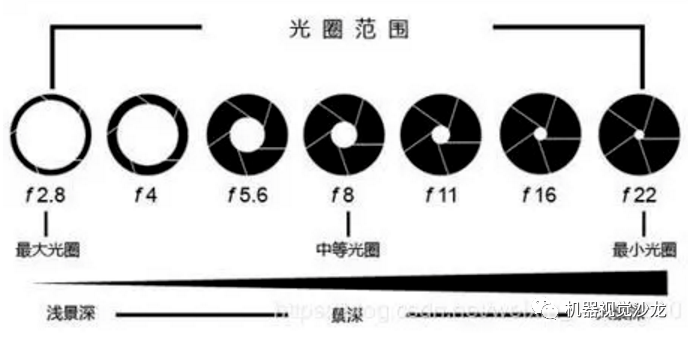
景深

景深（DOF），在聚焦完成后，焦点前后的范围内所呈现的清晰图像，这一前一后的距离范围，便叫做景深。

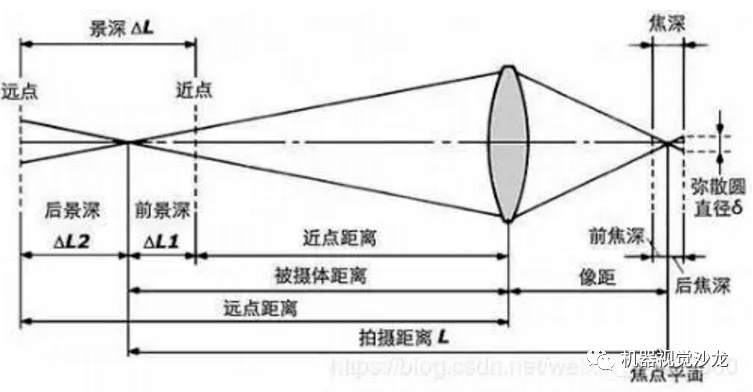
光圈、镜头、及拍摄物的距离是影响景深的重要因素。

1）光圈越大（f值），景深越浅，光圈越小（f值）景深越深。

2）焦距越长，景深越浅、反之景深越深。

3）主体越近，景深越浅，主体越远，景深越深

曝光

是指在摄影过程中进入镜头照射在感光元件上的光量，由光圈、快门、感光度的组合来控制。

视场角

视场角在光学工程中又称视场，视场角的大小决定了光学仪器的视野范围。

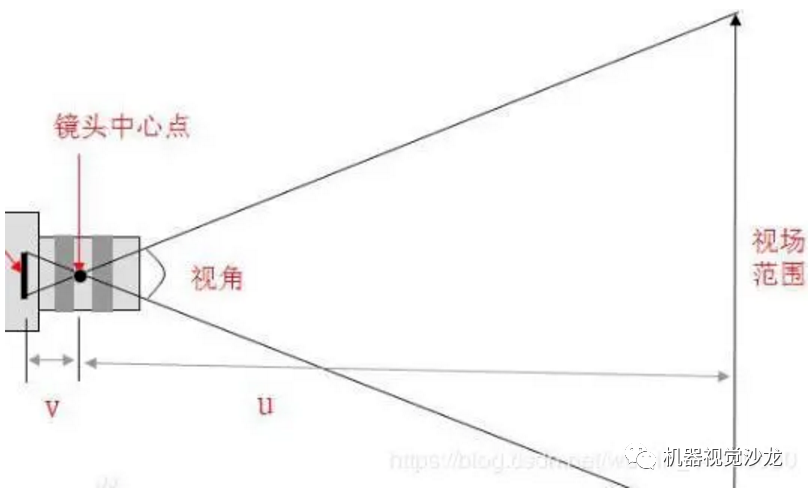
一般视场角越大视野范围越大，视场角越小视野范围越小。

视场角大小因焦距而变化，焦距越近视场角越大，焦距越远视场角越小。

分辨率

分辨率代表镜头记录物体细节的能力， 以每毫米里面能够分辨黑白对线的数量为计量单位 ：“线对/ 毫米”（lp/mm）。分辨率越高的镜头成像越清晰。

数值孔径

数值孔径等于由物体与物镜间媒质的折射率 n 与物镜孔径角的一半（a2）的正弦值的乘积，计算公式为 N.A=n*sin a/2 。数值孔径与其它光学参数有着密切的关系， 它与分辨率成正比， 与放大率成正比。也就是说数值孔径，直接决定了镜头分辨率， 数值孔径越大，分辨率越高，否则反之。

后背焦

准确来说， 后倍焦是相机的一个参数， 指相机接口平面到芯片的距离。但在线扫描镜头或者大面阵相机的镜头选型时， 后倍焦是一个非常重要的参数，因为它直接影响镜头的配置。不同厂家的相机，哪怕接口一样也可能有不同的后倍焦。

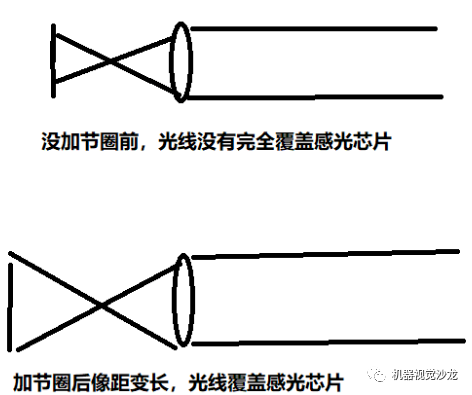
节圈的作用

加与不加节圈都不会影响相机的焦距，焦距本身是镜头固有的属性。

相机接圈，可以增大焦平面到镜头的距离，使镜头拍摄物体的距离更近，相当于微距摄影，成像更大。

一般来说，镜头畸变实际上是光学透镜固有的透视失真的总称，也就是因为透视原因造成的失真，这种失真对于照片的成像质量是非常不利的，但因为这是透镜的固有特性（凸透镜汇聚光线、凹透镜发散光线），所以无法消除，只能改善。

枕形畸变

枕形畸变（Pincushion Distortion），又称枕形失真，它是由镜头引起的画面向中间“收缩”的现象。我们在使用长焦镜头或使用变焦镜头的长焦端时，最容易察觉枕形失真现象。

桶形畸变

桶形畸变（Barrel Distortion），又称桶形失真，是由镜头中透镜物理性能以及镜片组结构引起的成像画面呈桶形膨胀状的失真现象。我们在使用广角镜头或使用变焦镜头的广角端时，最容易察觉桶形失真现象。

远心镜头

远心镜头（Telecentric），主要是为纠正传统工业镜头视差而设计，它可以在一定的物距范围内，使得到的图像放大倍率不会变化，这对被测物不在同一物面上的情况是非常重要的应用。远心镜头由于其特有的平行光路设计一直为对镜头畸变要求很高的机器视觉应用场合所青睐。

 

远心镜头光路的特点是，几乎进入到镜头的光都是强反射光。

非远心镜头成像效果：

非远心镜头成像效果：

远心镜头成像效果：

远心镜头主要弥补非远心镜头的以下特点：

1、由于被测量物体不在同一个测量平面，而造成放大倍率的不同；

2、镜头畸变大

3、视差也就是当物距变大时，对物体的放大倍数也改变；

4、镜头的解析度不高；

5、由于视觉光源的几何特性，而造成的图像边缘位置的不确定性。 

远心和非远心各自的优点：

普通镜头优点：成本低，实用，用途广。

普通镜头缺点：放大倍率会有变化，有视差。

普通镜头应用：大物体成像。

远心镜头的优点：放大倍数恒定，不随景深变化而变化，无视差。

远心镜头的缺点：成本高，尺寸大，重量重。

远心镜头的应用：度量衡方面，基于CCD方面的测量，微晶学。

当检查物体遇到以下6中情况时，最好选用远心镜头：

1、当需要检测有厚度的物体时（厚度>1/10 FOV直径）；

2、需要检测不在同一平面的物体时；

3、当不清楚物体到镜头的距离究竟是多少时；

4、当需要检测带孔径、三维的物体时；

5、当需要低畸变、图像效果亮度几乎完全一致时；

6、当缺陷只在同一方向平行照明下才能检测到时。