MOS表现出理想模型所没有的各种二阶效应。为了设计在现实世界中工作的模拟集成电路，我们需要了解这些非理想因素。

在上一篇文章中，我们介绍了基本的MOSFET结构和工作区域。我们讨论的模型描绘了一个理想的MOSFET，并且由于其较长的沟道尺寸，对于早期的MOSFET来说是相当准确的。然而，随后的研究和的持续小型化都揭示了行为中的一系列非理想性。本文将介绍这些非理想性的基础知识以及它们如何影响模拟集成电路中的晶体管性能。

寄生电容

由于MOSFET的物理实现，在端子结之间形成了以下寄生电容：

CGS：栅源电容。

CGD：栅极到漏极电容。

CGB：栅极到本体电容。

CSB：源极到体电容。

CDB：漏极到体电容。

在设计包含MOSFET的模拟IC时，这些电容在电路带宽中起着重要作用。图1显示了它们的位置。

带有寄生电容的NMOS晶体管结构。

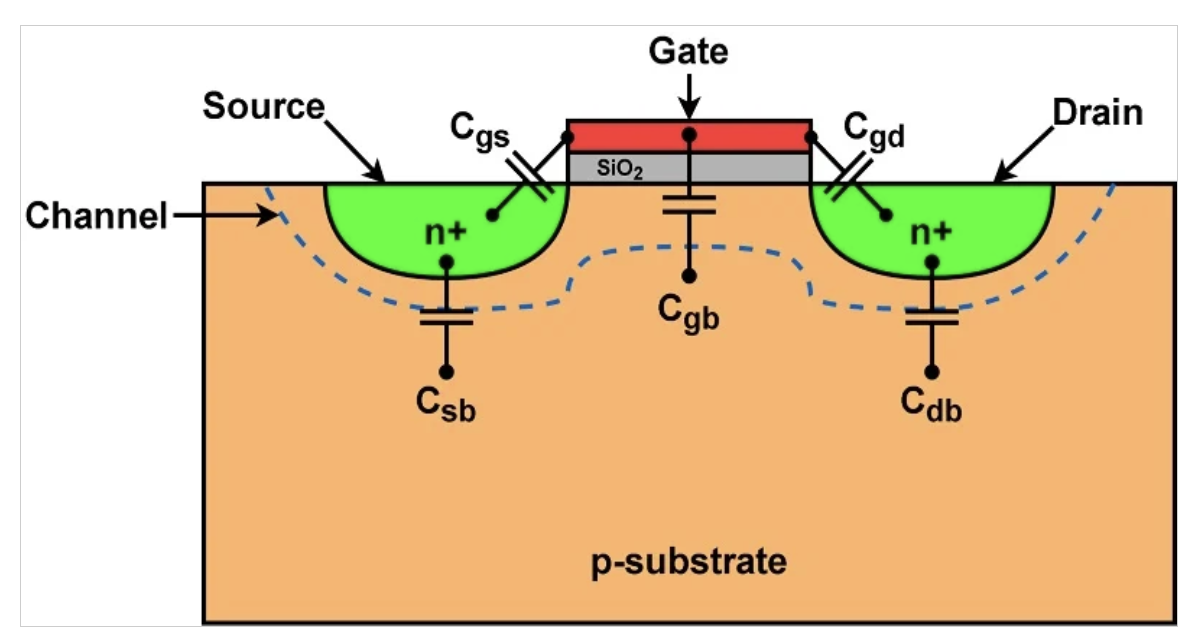
图1.具有寄生电容的MOSFET结构。

电容值会随着工作区域的变化而变化，我们将在接下来的部分中讨论。

栅源和栅漏电容

虽然图1中没有显示，但在晶体管制造过程中，源极和漏极在栅极下方略微延伸。在栅极与源极或漏极重叠的区域，栅极氧化物（SiO2）作为它们之间的电介质形成电容器。这种重叠的长度称为Ldiff。

由氧化物电容（Cox）形成的栅极到源极（或漏极）电容的值可以计算为：

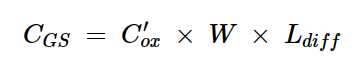
方程式1

其中：

C'ox等于 ϵox/tox

εox是二氧化硅的介电常数

tox是栅极氧化层的厚度（图1所示的高度）。

这个简单的栅源（或漏极）电容方程仅在源极和漏极彼此分开时有效，当晶体管处于截止或饱和状态时（由于沟道夹断），这是正确的。在线性区域，源极和漏极沟道被电阻沟道有效地“短路”，所以我们只需要关注栅极和沟道之间的氧化物电容。

由于器件是对称的，在线性区域，我们可以假设源极和漏极各占氧化物电容值的一半。栅极到源极和栅极到漏极的值可以计算为：

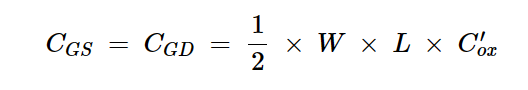
方程式2

栅极-本体电容

CGD的值实际上由两个单独电容器的并联组合组成：

氧化物电容器，位于栅极和衬底之间。

耗尽电容器，形成于耗尽层（沟道和衬底之间的区域）和衬底之间。

氧化物电容值可以使用以下方程式计算：

方程式3

和耗尽电容，使用这个：

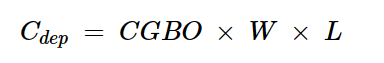
方程式4

其中CGBO是栅极-体块重叠电容项，取决于晶体管的物理特性。

氧化物电容和耗尽电容彼此并联——当两者都存在时，它们会加在一起。在截止区，由于栅极和本体之间没有沟道，CGB的值是方程3和4的总和。一旦出现沟道，Cox就会与本体断开连接，正如我们之前讨论的栅极到源极/漏极电容。因此，CGD的值等于Cdep，并且可以使用方程4来计算。

源极至本体和漏极至本体的电容

推导CSB和CDB的值涉及大量的器件物理学。这些值由结电容（CJ）决定。CJ的值由耗尽区宽度决定，而耗尽区宽度又基于MOSFET内的掺杂浓度。

我们需要从这一点中得出结论，即CSB和CDB在源极或漏极与主体之间的交界处保持不变，因为工作区域之间的端子尺寸不会发生变化。

电容值总结

表1总结了MOSFET的寄生电容值（按操作区域）。

表1.寄生电容值。

身体效应

我们之前讨论过晶体管的体端和源端通常如何连接到相同的电势，但没有解释为什么是这样。为了理解原因，让我们更深入地研究物理晶体管，当VGS的值从0增加到大于阈值电压（Vth）时。

当VGS从零缓慢增加时，硅中的正空穴被推离栅极，留下带负电的离子。这产生了一个耗尽层——一个没有载流子的区域。随着VGS继续增加，栅极电荷开始慢慢超过耗尽层，因此在源极和漏极之间可以形成一个电子通道。

假设体电压变得比源极更负（VSB>0）。现在更多的空穴被吸引到体端子，导致在沟道附近形成更大的耗尽区。这意味着阈值电压的增加，因为现在需要更大的栅极电压来克服耗尽区的电荷并形成沟道。当VSB<0时，情况正好相反：在沟道附近形成较小的耗尽区，Vth相应地降低。

体效应如图2所示。

MOSFET中体效应的一个例子。

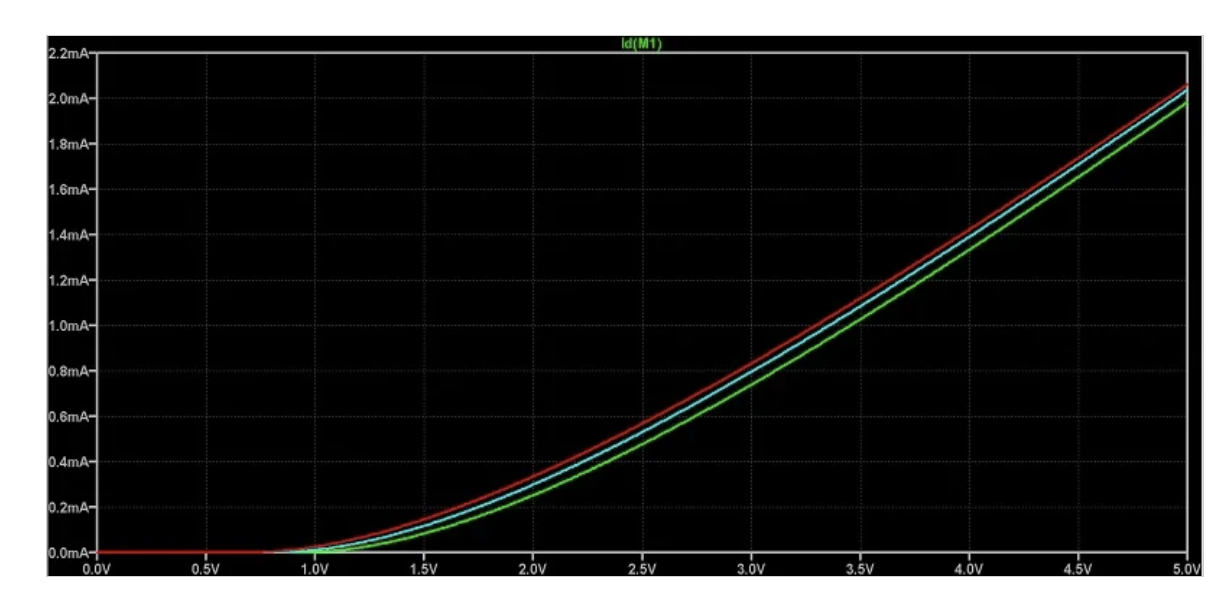
图2:ID与VGS在不同VSB下的对比（浅蓝色：VSB=0V；绿色：VSB=-0.5V；红色：VSB=0.5V）。

相对于体效应的阈值电压可以计算为：

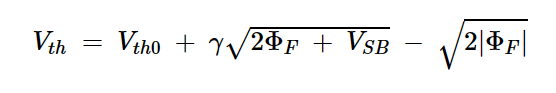
方程式5

其中：

Vth0是标称阈值电压

ΦF是硅的费米势。

体效应对模拟设计有很大影响——堆叠晶体管是非常流行的，这会导致体效应以一种非平凡的方式改变阈值电压。

信道长度调制

理论上，饱和状态的晶体管应作为具有无限输出电阻的理想电流源。 实际上，当沟道收缩时，VDS仍对漏极电流有影响，因此晶体管的输出电阻虽然很大，但仍然是有限的。 这是由于一种称为沟道长度调制的现象，其中在饱和区域中，随着漏极电压的增加，沟道长度开始逐渐减小。

为了适应沟道长度调制，我们将饱和状态下的漏极电流方程调整为：

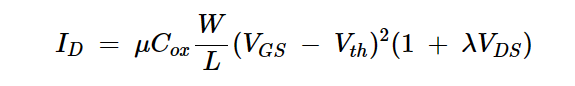
方程式6。

信道长度调制系数λ的计算公式为：

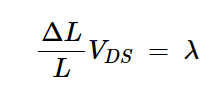
方程式7

由此，我们可以计算饱和时的输出电阻（ROUT）为：

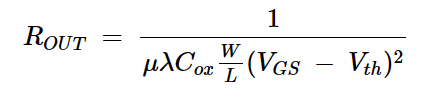
方程式8

亚阈值导电

以前，我们定义了三个晶体管工作区域：截止、线性、饱和。实际上，还有第四个：亚阈值区域，它在超低功耗模拟集成电路设计中非常流行。

该区域的形成是因为晶体管在VGS低于Vth时不会完全关闭。相反，扩散电流在源极和漏极之间形成了一个小沟道。当VGS < Vth时，这种扩散电流是不可忽视的，并且与VGS呈指数关系。由此产生的亚阈值区域的I-V曲线计算如下：

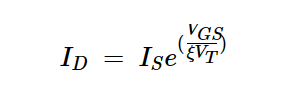
方程式9

其中：

IS是晶体管的特定电流，与W/L

ξ为非理想系数（硅中>1）

VT是热电压，等于kT/q

迁移率退化和速度饱和

晶体管内的漂移电流由内部电场决定，随着晶体管尺寸的减小，它们的电场迅速增加。事实证明，对于短沟道晶体管，在晶体管内可以实现少数载流子的最大速度。这被称为饱和速度。

这限制了某些器件的VGS和VDS电流的增加，因为最终它们的驱动电流达到最大值。此外，随着电场的继续增加，这些载流子的迁移率降低，导致这些极高电压下的驱动电流减小。这种短沟道效应是现代晶体管行为的许多方面之一，我们无法通过前一篇文章中研究的平方律方程来预测。

排水诱导屏障降低（DIBL）

当VDS变得足够大时，漏极开始将负电荷吸引到栅极下的表面，帮助栅极形成沟道。因此，有效阈值电压降低，从而形成Vth与VDS成反比的关系。这被称为漏极诱导势垒降低，简称DIBL。

PVT变化

工艺、电压和温度的变化统称为PVT，共同构成了我们讨论的最后一个非理想因素。

在制造晶体管时，制造工艺变化是不可避免的。工艺变化会改变重要的晶体管特性，导致不同的阈值电压、载流子迁移率和寄生电容等。这些工艺变化通常包含在四个“角落”：快-快、快-慢、慢-快和慢-慢。这些角落描述了基于最坏情况制造统计数据的PMOS和NMOS晶体管的相对速度。

除此之外，通过蒙特卡洛分析测试晶体管之间的差异，该分析使用包含所制造晶体管参数变化统计数据的模型。模拟设计人员必须同时使用蒙特卡洛和拐角方法，因为失配会对电路性能产生破坏性影响。

最后，工作电压和环境温度也会影响晶体管性能。在IC设计过程中必须检查这些环境条件，以确保最终产品按照规格运行。