极值搜索控制是一种基于最优极值搜索的自适应控制算法。它的核心思想是通过优化性能指标来调整控制器的参数，以逐步实现对系统的自适应调节。该算法通常应用于具有不确定参数或无法精确建模的非线性系统中。
极值搜索控制方法可以分为两个阶段：第一阶段是建立系统的数学模型，通过计算性能指标的梯度信息，确定初始控制器的参数；第二阶段是基于迭代寻优的方式，使用最优极值搜索算法不断微调控制器的参数，以实现控制系统的自适应调节。
在极值搜索控制的第二阶段中，常用的寻优算法包括梯度下降法、牛顿法、共轭梯度法等。这些算法可以根据指定的准则来调整控制器的参数，使得系统的性能指标得到最优化。其中，多参数极值搜索方法是一类基于多参数函数的全局极值搜索算法，可以在保证全局收敛
极值搜索过程
经过Simulink验证，这种方法可以在未建立模型的情况下搜索到极值点。
极值搜索控制
下图所示的是应用于控制系统的极值搜索控制的框图。由于ESC需要追踪极小值或者极大值，如果搜索信号过于平滑，则会影响搜索过程，所以相较于上述的极值搜索过程，在控制系统与极值搜索环节之间添加了一个高通滤波器，用于减小来自被控对象的低频干扰对极值搜索过程的影响。
极值搜索控制属于数据驱动控制方法，不必如同其他控制方法讲述模型建立的过程，因此下面将通过两个具体实例帮助读者理解。
不确定线性系统的自适应增益调整
该系统应用极值搜索控制方法的框图如下：
搭建Simulink仿真模型.
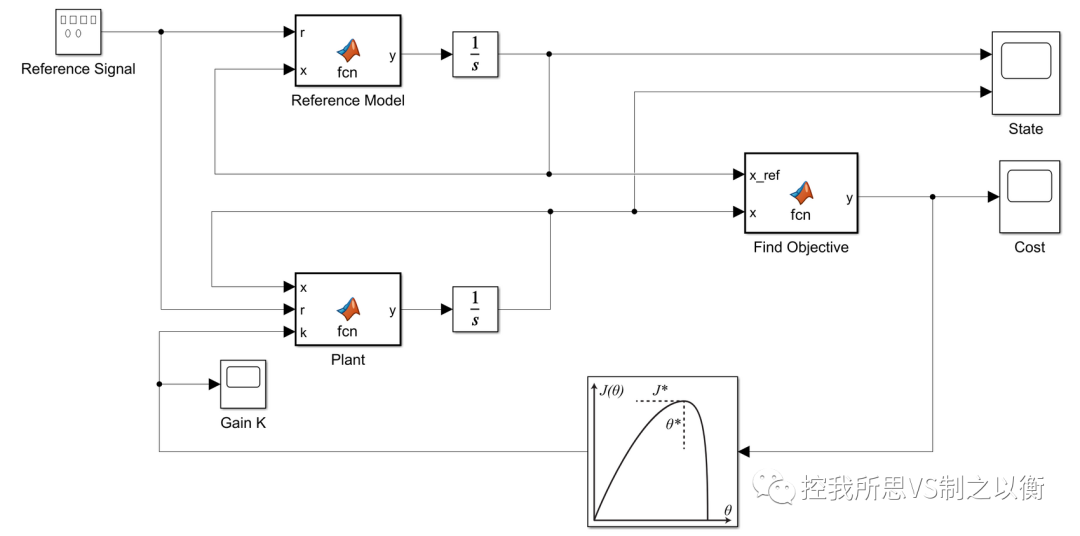
参考输出和实际输出如下所示
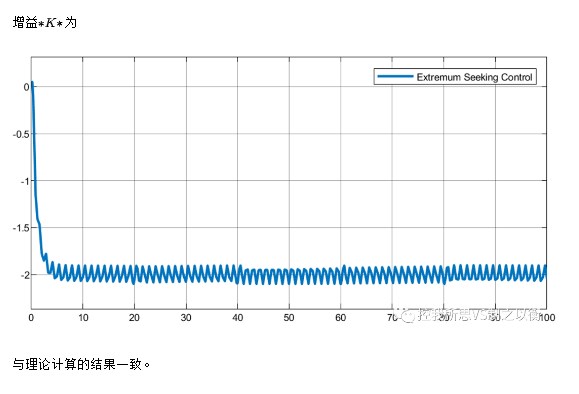
使用极值搜索控制实现防抱死刹车（ Anti-Lock Braking ）
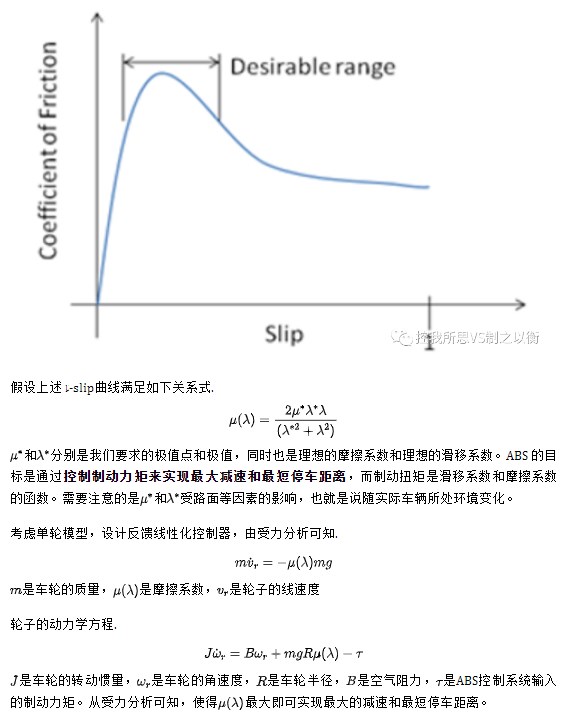
使用极值搜索控制实现防抱死刹车的模型如下所示.
进行Simulink仿真，控制器为
function tau = fcn(v,w,lambda0,vdot,lambda)
m = 400;
B = 0.01;
R = 0.3;
I = 1;
c = 2;
if v<= 0.001
tau = 0;
end
tau = -c*I*v/R*(lambda-lambda0)-B*w-I*w/v*vdot-m*R*vdot;
仿真结果
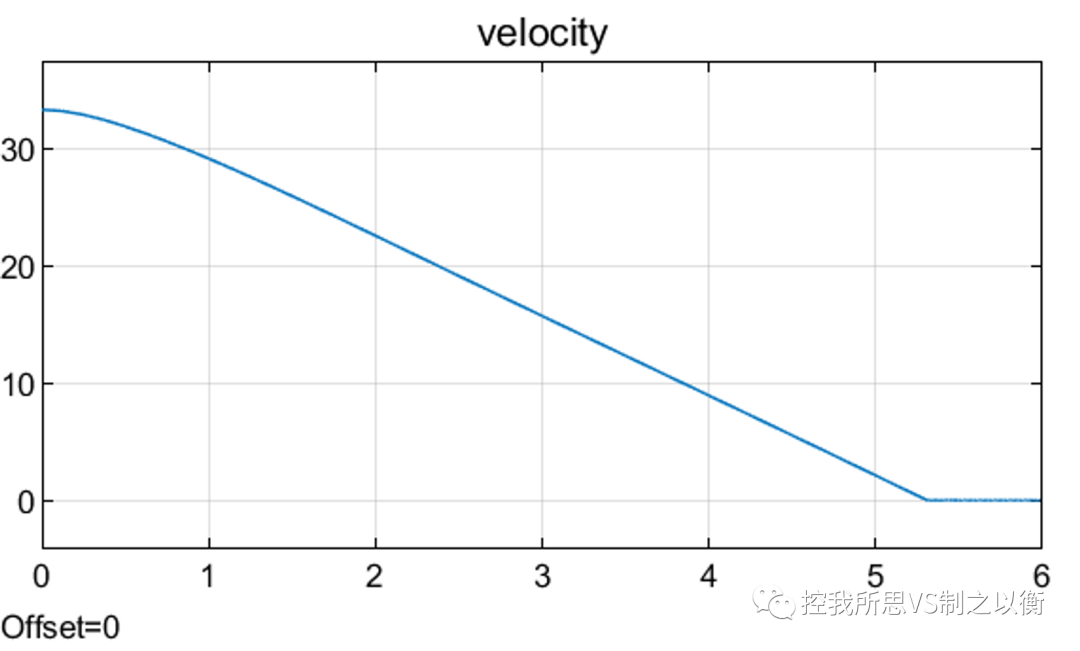
通过上述两个仿真案例可知，可总结出极值搜索控制适合于如下几个应用场景：
系统优化过程：代价函数为非线性或非线性系统，用解析的方法不不容易找到代价函数的局部最优.
复杂系统：搜索状态空间找到最优控制策略.
模糊系统：用来找最优解（注意不是模糊控制，指有很多未建模动态的系统）.
多变量系统：极值搜索方法可以通过考虑多个变量之间的相互关系，来确定最优控制策略.
极值搜索控制的缺点也十分明显，包括陷入局部最优无法发现全局最优解、搜索过程较慢、对初值的依赖度高、参数的确定。
