本文以线性伺服电机的用例说明了比例积分微分 (PID) 控制，包括其背后的数学原理。

通过本文你将能了解到：

PID 控制的基础知识。

电路中连接元件以完成位置控制的 PID 功能的那些部分的注意事项。

固件

代码实现。

比例积分微分 (PID) 控制是用于调节系统动态行为的常用方法。在许多工业设备中都可以找到示例，其中它用于控制温度、压力、流量、速度或位置等。 PID 控制背后的理论和数学一直是很多讨论的主题。但是如何应用这些数学和理论来实现一个真实的设备呢？为了演示这是如何完成的，本文将探讨一个完整的示例。

位置控制的任务将针对线性伺服电机的情况进行讨论。首先，介绍控制 PID 控制器运行的数学函数。我们将展示函数的各个部分如何在实际设计中组合在一起。具体来说，我们将解决电路中接口元件的注意事项，以完成用于位置控制的 PID 功能的那些部分，以及在将执行控制的微控制器的固件代码中实现该功能所涉及的内容。

PID 基础知识

作为任何 PID 控制应用基础的通用数学函数可以表述如下：

其中e(t)是偏差值：

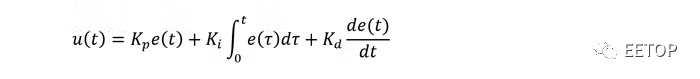
对于位置控制，r(t)为设定位置，y(t)为当前位置。

一张图可以让我们更直观地理解这个数学在应用于伺服电机时是如何工作的。图 1说明了线性伺服 PID 控制系统的框图。

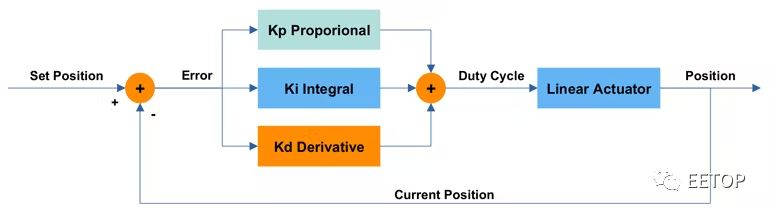
图1、线性伺服PID控制系统。

图 1中描绘的系统的一些关键元素是设置位置输入（设定点，或我们的线性执行器的目标位置）、驱动执行器的某些占空比的脉冲宽度调制 (PWM) 信号，以及执行器的当前位置。它们分别对应于数学方程式中的量r(t)、 u(t)和y(t) 。

之所以称为闭环控制，是因为反馈回路将有关当前状态的信息传递回系统，使其能够获得当前状态与所需设定点之间的差异，必须对其进行校正。具体到我们的案例，从设置位置中减去当前位置以获得误差（或偏差）信号，如上所示。此误差对应于数量e(t)。

正如文章开头提到的，PID 代表比例、积分和微分。这些是指为调节 PID 控制系统的运行而生成的三个控制信号。

如数学和图表所示，三个控制信号由误差信号产生，从Proportional、Integral和Derivative模块输出——也标有它们各自的增益K p、K i和K d ——并且是结合起来产生驱动执行器的 PWM 信号的占空比。

现在我们已经描述了系统的结构，我们想在固件中实现它。但要做到这一点，我们需要了解如何将线性致动器与微控制器连接起来。具体来说，我们如何从PID函数中获取Duty Cycle信号来驱动执行器，以及执行器如何产生Current Position信号反馈给PID函数？

随后，我们可以解释如何将PID函数翻译成用C语言编写的固件源代码。然后将提供一些演示工作实施的示例数据，作为理解三个 PID 控制信号的作用以及如何调整其性能的基础。

电气连接线性致动器

线性致动器用于提升、倾斜、拉动或推动物体（图 2）。我们这里使用的微型线性执行器由驱动部分的直流伺服电机和位置传感部分的电位器组成。

图2. 线性致动器的示例。

对于该装置，PID 控制器板需要输出 12V PWM 信号来控制电机速度，并使用模数转换器 (ADC) 通道来感测执行器的位置。因此，我们应该在微控制器上配置两个 GPIO 引脚，一个用于 PWM，另一个用于 ADC。

线性执行器的位置输出是一个电阻值。如果电位器连接在电源V dd和地GND之间（图 3），则可以将抽头处的电阻作为简单分压器的输出进行测量。位置的范围和单位从 0 ~ 10,000 Ω 对应为 0 ~ V dd V，ADC 将电压转换为数字值，即我们实现的当前位置y(t)。如果 ADC 的分辨率为 10 位，则此数字值介于 0 和 1023 之间。

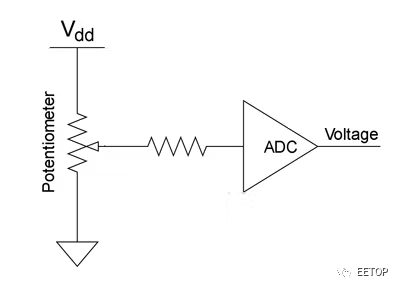
图3、电位器ADC电路。

我们的控制器输出u(t)也可以是表示电压的数字值，这很方便。然而，该控制器输出驱动线性致动器，线性致动器不期望变化的电压作为输入来控制其速度，而是期望具有变化占空比的固定电压 PWM 信号。因此，需要进行转换。

图 4中的图表显示了 0 V 至 12 V 的电压如何转换为具有 0% 至 100% 占空比的可变宽度脉冲的 12 V PWM 信号。严格来说，高于 12 V 的电压也必须考虑在内，并且必须转换为 100% 的占空比，因为数学决不会将控制器输出限制在 12 V 以下。

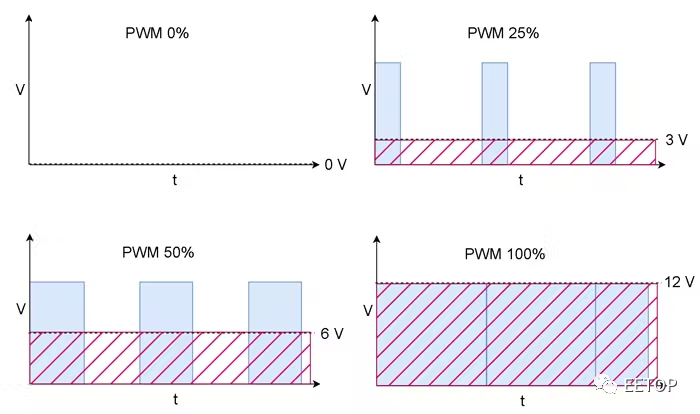
图4. PWM 信号图。

作为关于执行器接口的最后评论，我们应该强调，只有我们选择的设备的速度控制和位置传感特性的性质引导我们将 u(t) 和 y(t) 都指定为我们实施中的电压值。这些数值没有其他关系，如果受控设备接口的性质另有规定，在另一个应用程序中甚至可能不在同一测量单位中。

编写固件

对于用作 PID 控制器的固件，它必须确定误差值e(t)，评估 PID 函数以调整驱动设备的信号u(t) ，并随着时间的推移连续执行此操作。然而，对于固件执行而言，以真正连续的方式执行任务并不是一个可行的概念。最接近的是在很短的时间间隔内快速重复或迭代任务。 

如果该任务是 PID 算法，则其连续时间数学需要用离散时间版本替换，具有以下含义：

1. 固定间隔T被指定为迭代之间的时间，即它们的周期。

2. 将连续时间t时刻的误差值e(t)的评估替换为离散时间迭代n时的评估，即e(n) = r(n) – y(n)，其中n = 0 , 1, 2, …

3. e(t)的连续时间积分由e(n)T的离散时间求和代替。

4. e(t)的连续时间导数替换为e(n)在前一次迭代和当前迭代之间的线性斜率——即：

因此，在第n次迭代中评估的离散时间输出信号u(n)可以表示如下：

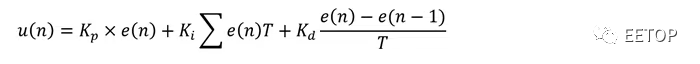
现在我们可以实现离散时间PID控制功能了。在示例 C 代码（参见下面的代码列表）中，变量和常量的名称与数学方程式中的相应元素非常匹配。此代码可以在 PID 固件的每次迭代中执行，通常在配置为每T毫秒触发一次的定时器中断内执行。

/* 当前误差- 比例项 */

e = r - y;

/* 累积误差- 积分项 */

总误差 += e;

/* 差分误差- 导数项 */

deltaError = e - 先前的错误；

/* PID控制*/

u = Kp * e + Ki * (totalError * T) + Kd * (deltaError /T);

/* 同时为下一次迭代做准备——将之前的设置为当前错误 */

以前的错误= e；

剩下要做的是为 PID 增益K p、K i、和K d以便系统在被要求移动到选定的设定点时正确执行。我们将为这些增益手动选择不同的值，以研究它们对位置控制的影响，并在此过程中演示调整它们的通用方法。我们还将深入了解控制功能中每个术语的用途。

PID 增益调整

有几个评估系统性能的标准，包括死区时间、上升时间、过冲、稳定时间和稳态误差。虽然在调整 PID 增益之前应根据这些标准定义性能预期，但此类预期取决于应用程序的要求。因此，就本文而言，足以说明各种标准何时受到不同增益调整的影响。

Kp , K i , _和Kd增益将单独调整，并按此顺序，给定一个选定的设置点。更具体地说，代码将在每次执行时将其中一个增益设置为不同的值，并将 r 的值设置为 700。

至于这个 700 值的相关性，读者应该记得Current Position是一个数字值，表示从执行器的电位器获得的电压，而Current Position现在在我们的代码中由变量 y 表示。设置位置-表示我们代码中的变量 r - 是相同范围内的数字值，如前所述，如果 ADC 具有 10 位分辨率，则该值介于 0 和 1023 之间。因此，700 的设定点值是合理的，尽管是任意的。

调整 K p以接近目标位置

Kp是比例增益。控制函数的比例项通过使用与该电流误差成比例的信号移动线性致动器来补偿电流误差。比例项用于使当前位置接近目标是有意义的，因为该误差是执行器的设定位置与其当前位置之间的差异。比例项使控制函数寻求将其减少到零。

在调整的第一步中，我们将积分和微分增益K i和K d设置为零，并增加比例增益K p直到致动器稳定在目标位置附近 (700)。比例增益太高会引起振荡。

图 5中的图表显示了对于不同的K p值，执行器的当前位置如何随时间变化。我们将选择K p = 1，观察它会导致当前位置稳定在目标附近并且稳定时间最快。

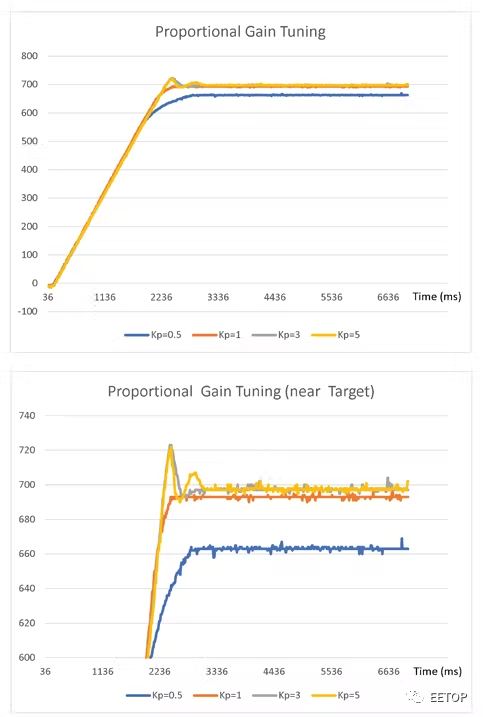
图5.比例增益调整。

读者会注意到有一个残余的稳态误差，即最终的当前位置与目标设定点位置有偏差。这种偏移在纯比例控制器的情况下很常见，并且会在下一步调整积分增益时消除。

调整 K i以消除稳态误差

Ki是积分增益。控制函数的积分项通过使用与随时间累积的过去误差量成比例的信号移动线性致动器来补偿过去误差。积分项用于消除稳态误差是有意义的，因为该误差是一个常数偏移量，它会随着时间的推移增加积分，从而使控制函数试图将其减小到零。

在调整的第二步中，我们保持在第一步中选择的比例增益K p = 1，将微分增益K d设置为零，并增加积分增益K i直到执行器稳定得更接近目标位置 (700) ——即，直到稳态误差接近于零。

图 6中的图表显示了对于K p = 1 的不同K i值，执行器的当前位置如何随时间变化。对于一组给定的要求， Ki = 0.5的结果可能非常令人满意，我们可能会选择不涉及微分项，在这种情况下，解决方案将是比例积分 (PI) 控制器。

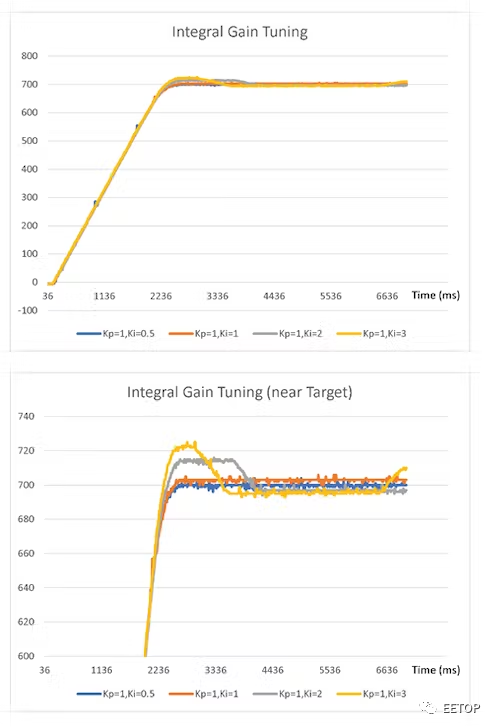
图6.积分增益调整。

但是，或者，我们可能更愿意选择K i = 2，这可能是由于其结果中显示的上升时间有所改善。读者会注意到，在这种情况下，更好的上升时间是以过冲为代价的。当在下一步中调整微分增益时，将消除这种过冲。

调整 K d以消除过冲

Kd是微分增益。控制函数的导数项通过使用与根据误差的时间导数（即其变化率）估计的未来误差量成比例的信号移动线性致动器来补偿未来（估计的）误差。

微分项用于消除瞬态效应（如超调）是有道理的，它们自然反映在时间导数中，从而使控制函数寻求将它们减少到零。在存在干扰的情况下提高稳定性和缩短建立时间是额外的相关优势。但是请注意，如果误差信号非常嘈杂，微分项会使控制系统不稳定。

在这第三步调整中，我们保持在前两步中选择的比例和积分增益K p = 1 和K i = 2，并增加微分增益K d直到消除超调。微分增益太高会引起振荡。

图 7中的图表显示了对于不同的K d值，K p = 1 和K i = 2 ，执行器的当前位置如何随时间变化。我们将选择K d = 0.05，观察到它有效地减少了过冲，同时保持了改进的上升时间。

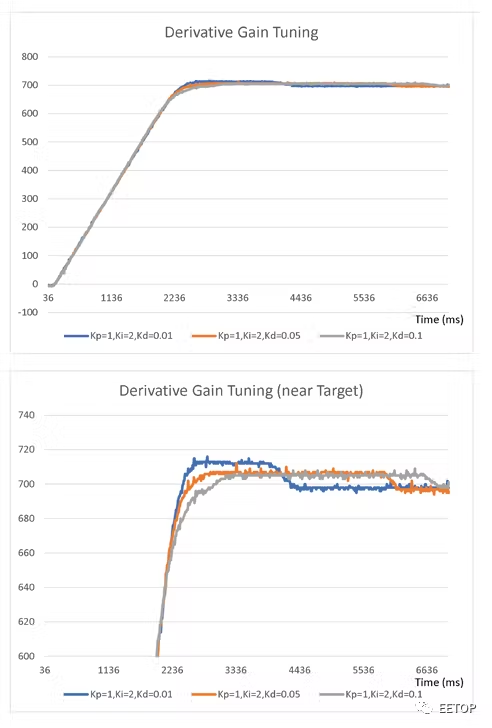
图7. 微分增益调整。

然后，在我们的控制器版本中，启用了所有三个信号比例、积分和微分，我们已经成功地调整了它们的增益以实现适当的控制器行为。我们还确定增益值应为K p = 1、K i = 2 和K d = 0.05。

结论

这篇关于 PID 控制的文章解释了 PID 控制器核心的数学原理，并提供了一个实际示例，说明如何实现该数学原理以在微控制器上运行。讨论了用于位置控制的微控制器和直流伺服电机之间的信号性质的实际考虑因素。

最后，提供了一些数据来演示如何手动调整控制函数的比例、积分和微分项以获得适当的性能。它还让读者了解 PID 算法中每个函数的用途。

通用现成的 PID 控制器不是将 PID 控制设计到定制的嵌入式设备中，而是工业市场上可用的替代品，例如，其中一些基于可编程逻辑控制器 (PLC)。这些可能会满足许多用户的需求。

但是，如果它需要与您的工厂流程相关的非标准功能，它可能无法满足您的应用需求。或者，如果它有特殊的数据通信需求，或者如果通用控制器具有您希望避免用于成本敏感型应用的不需要的功能。在这种情况下，定制 PID 控制器设计是一种选择。（EETOP编译自electronicdesign）