pid算法概述

过程控制中有两个重要的算法PID反馈算法，卡尔曼状态估计算法。PID主要用来过程控制，卡尔曼滤波主要用来状态估计，比如预测运动轨迹之类的。这一篇我们主要分享PID算法。

什么是pid算法呢？PID分别表示比例P，积分I，微分D。比例。积分，微分，计算的都是误差或者目前的值和期望的值之间的差异，变化率，均值等。该算法主要用于过程控制。

学过信号与系统或者自动化控制的应该都多多少少记得状态方程，给一个系统加上输入，然后得到输出。输出和输入有明确的函数关系。y=f(x);这个函数的计算过程就是该系统的固有属性。比如我们设计滤波器，根据运动规律得到一个弹簧滑块的力学计算公式。给滤波器输入会得到输出，给弹簧滑块弹簧一个力，弹簧滑块会按照一定的规律运动。模拟滤波器的阻抗匹配电路连接规律决定了该滤波器的固有属性。弹簧滑块的质量，弹性系数，摩擦系数等决定了该力学系统的固有属性。该固有属性就是y=f(x);给一个输入x会得到一个输出y。可以看到抛开是具体的应用场景是信号还是力学系统，背后的数学模型是一样的。

那么这个和PID有啥关系呢？要解释这个我们先要解释反馈。数学模型是理想的模型，但是实际的使用场景不会这么理想，我们设计的模拟滤波器，计算好了电阻，电容连接好了电路。但是电阻和电容都不是理想的器件，更何况外界包括电路本身还有电磁干扰。工厂生产的5欧姆的电阻不可能就没有误差就是5欧姆。随着电路的使用发热空气湿度电阻的大小也会变化，同样的电容也是。加上外界干扰情况就更加的复杂。同样的力学系统，我们也是理想情况，1千克的滑块，不可能就完全是1千克，弹簧的弹性系数随着使用也不是严格确定的值，摩擦系数也不会没有误差。所以就需要引入反馈系统。

1，举例解释pid算法

结合具体的使用场景， 学习过模电的应该都多少有点印象，电路为了减少温度漂移带来的影响，引入了反馈，当输入不够或者过大的时候，通过反馈可以增加或减少输入，作为补偿。这样的电路更加有稳定性 。

那么PID和反馈有什么关系呢？ 可以说PID算法就是一个基于反馈的算法 。通常用于过程控制。只不过PID通常的使用场景比刚才说的滤波器里面的反馈有一点不同，刚才的滤波器我们的阻抗匹配设计好了滤波器的参数，也就是y=f(x)这个理想的数学模型已经有了，反馈是为了提高系统的稳定性。

但是通常情况下PID使用的场景是一个不确定的系统。比如我们期望将一杯水加热到60度，并且一直维持在60度。这个时候电热丝加热就是该水杯系统的输入，输出就是温度值。但是希望这杯水的温度就是一直维持在60度，不能高不能低(当然有一定的误差)。这个水杯就是一个系统，我们给水杯加热我们当然列不出来一个y=f(x)的一个状态方程。或者很难列出来。所以这个时候水杯对我们来说就是一个黑盒子。

如下图

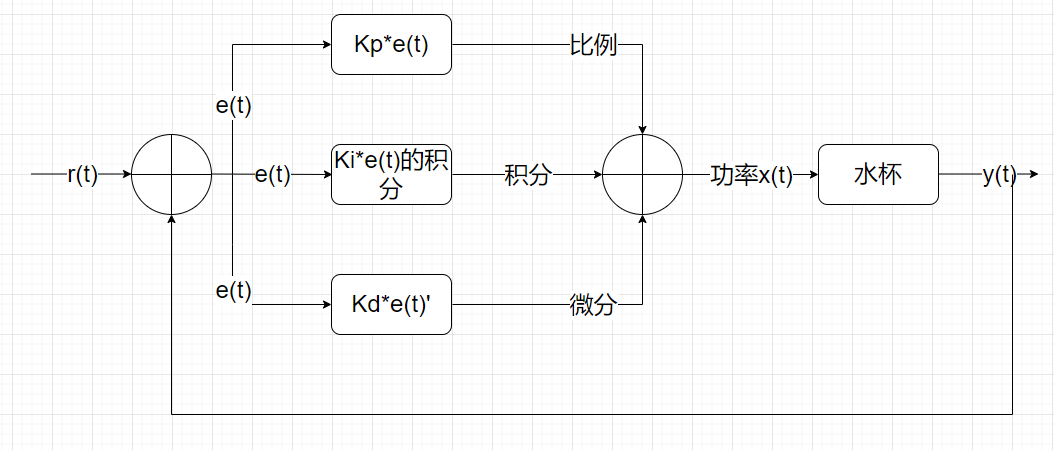
pid算法

图中r(t)就是我们的目标温度60度，y(t)是传感器的测量温度，x(t)是电热丝的功率，e(t)=r(t)-y(t)。也就是目标温度和当前实际温度的差。

右侧的水杯加热部分就是一个黑盒子，我们并不知道他的状态方程y=f(x)；也就是水杯是我们需要控制的黑盒子

那么我们怎么做到水杯里面的水加热到60度之后一直维持在一个很小的误差范围呢？我们肯定是通过不断地调节电热丝功率来实现的。当水的温度低于60度了就加大功率，当温度开始降低了，就降低功率。我们需要一个温度计来不断的测水的温度，然后和我们的期望温度60度做比较，进而决定控制电热丝的功率。这不就是反馈吗？

当温度低于60度加大功率，当温度高于60度降低功率。仔细思考一下这样的控制对吗？显然不对，我们设想一下，刚开始一杯室温下的水，温度是25度，这个时候不到60度，还差32度，所以我们加大功率，但是很快水温40度了，还差20度，我们还加大功率吗？显然不太合理。所以改进一下改为根据当前的水温和目标60度的差值，来决定输入的功率，设r(t)为我们的目标60度，y(t)是当前的测量温度，那么r(t)-y(t)就是当前和目标的U差值，所以我们是不是可以让功率受控于这个差值呢，x(t)=Kp(r(t)-y(t))+U常数，这样随着温度的升高我们的我们输入的功率x(t)会越来越小，直到一个常熟U，之所以有该常数是因为，我们不可能当温度到达60度的时候，就关闭了电热丝，因为水杯一直在在散热。所以有一个这样的常数，但是散热功率不能明确的就是这个常数U，因为周围哪怕来一股风，外界的环境是各种干扰的。所以就需要一会儿加大功率，一会儿减少功率。这个就是PID控制中的比例部分P。看起来似乎是可以控制，但是实际会发现温度在60度上下变化误差很大。

所以也就是这样的控制不够精细化，误差变化范围很大。如果温度是50多度，外界的散热环境也在实时变化，因为温度不够60度，所以肯定还是需要加热的，那么接近60度的时候功率还是挺大的，这样温度很快就超过60度了，可能会到65度，尽管我们降低功率了，但是热量的传输有一个过程，电阻丝还在加热。那么再想一下，还可以考虑哪些因素呢？我们思考一下为什么温度会很快超过60，然后我们才发现。然后才考虑降低，这样的控制，这个很快就是一个关键字。很快意味着速度，也就是温度上升的速度，这个是什么这个就是微分呀。所以我们可以从两个角度考虑既要考虑比例，又要考虑微分。比如刚开始一秒钟温度升高3度，后面一秒钟温度增加4度，然后是一秒钟增加2度。这个是温度增加的速度。所以当温度增加的速度快，快到达目标温度60的时候，我们是不是可以提前减速，这样后面超过了60度也不会超过很多。所以我们的输入改为x(t)=Kp(r(t)-y(t)+Kdy(t)’+U

这样我们的控制精确一些了，误差减少了。是不是还可以减少误差呢？有了比例和微分，这样我们的温度一直在60度上下波动。我们还可以考虑哪些因素呢？又是注意关键词语波动，在上下波动，也就是均值接近60，均值和什么相关呢，当然是积分。

令e(t)=r(t)-y(t),则整个PID的控制算法的公式可以改变为

所以最终的控制量就是x(t)=Kpe(t)+Kde(t)‘+Kie(t)积分+U

2，PID参数则确定

分析了PID的原理，那么公式中的Kp，Ki，Kd的确定通常是很麻烦的。首先不同的系统这个参数肯定不一样。所以这几个参数的大小肯定是受到原本系统的固有属性的影响的，以水加热来说，首先水的多少，是冬天还是夏天，周围空气的流动，水杯自身的导热程度等这些属性一定是间接的影响到这几个参数，正是因为系统的固有属性不能确定所以我们无法或者很难数学建模列出来y=f(x)。所以我们才需要借助反馈。不断地调整输入，使输出达到我们的期望。

通常的调节过程是先确定Kp的大概值，然后是Kd,再下来是Ki

以加热为例，首先我们调节Kp，使温度能快速的达到60度，但是肯定会过冲超过60度，为了能快速上升到60度，那么Kp就要调大一点，但是同样带来一个弊端就是温度可能超过60度很高，比如到80度了，所以通常都会有指标参数，比如最高温度不能超过多少度，达到60的时间是多少之类的。根据这个我们会选择一个比较合适的Kp。这个时候温度会在60度上下波动，但是误差很大，收敛很慢。

接着我们调节Kd，因为Kd是对温度上升速度的反应部分，结合Kd，能快速的降低误差，Kd是对观测量变化的体验，所以通常一个系统如果观测量变化很灵敏，很快，那么通常Kd就会很小。结合了Kp和Kd，这个时候系统的收敛速度能很快收敛，最高温度也会降低。但是系统还是很长一段时间在60度上下波动。为了进一步控制，接下来就要调节Ki参数了

Ki就是对波动的反应。能让观测量温度快速稳定在60度，同时误差也会小。

三个参数的调节是独立的，但是最后的输出是一个总的，所以当Ki调节完了，反过来又要适当的调节Kp，Kd，最终达到一个比较好的效果。

3,PID三个调节分量的优缺点

Kp调节的是宏观的，让系统快速的达到期望目标，Kd是对速度的反馈调节，能让系统快速的收敛，Ki是对考虑历史数据，是一个均值的作用，能减少毛刺，让系统基本稳定后的波动小一些。

但是凡是都有弊端，Kp过大，尽管能让系统快速达到期望值，但是同样的会过多的超过期望值。所以需要Kd对速度变化部分提供反馈控制

Kd对当前的速度做出反应，所以可以让观测值快速收敛，但是毛刺还是很多。

因为Ki部分求的是均值，会让系统很快稳定，但是尤其是最开始的时候偏差很大，历史的偏差会一直影响积分控制项，将这个残差一直留着，所以通常可以在系统最开始的时候不适用Ki，当系统达到期望值之后，开始加入Ki部分，这样能消除系统最早的最严重的偏差。得到更好的效果

我们还是以加热丝给水杯加热为例，我们在室内调好了PID的三个参数，然后我们拿到室外，或者开空调了，或者夏天调的参数在冬天使用，那么我们调的这几个参数可能会因为外部环境的变化可能就很难达到很好的效果。调节的参数总是有一定适用范围的，所以也是有方式自动调节PID参数的，做到PID参数的自适应的。

买来的一台大疆无人机，在空气流动不大，温度适宜的地方可以起飞，然后如果狂风大作，总不可能说大风的时候不能用了，需要重新调节参数，肯定是有自适应调节的。飞机刚开始感受到变化，比如突然大风开始刮起来了，这个时候飞机会短暂的不稳定，然后快速的稳定。