引言

配电网精益化管理是实现供电企业提质增效的有效措施,其中,正确的户变关系是开展配电网精益化管理的前提。当前低压配电网拓扑信息主要依赖人工录入,由于历史记录丢失、配变扩容与线路迁改时信息更新不及时等原因,低压台区档案混乱,台账中户变关系存在不少错误的情况,严重阻碍了台区故障定位、窃电核查、线损及三相不平衡治理等台区精益化管理工作的开展。因此,研究低压台区户变关系辨识方法具有理论价值与现实意义。

传统的户变关系辨识方法主要包括人工巡线法、瞬时停电法、特征信号法和台区识别仪法。但上述方法与配电网规模日趋变大、供电可靠性要求日益提高的发展趋势相矛盾,难以大规模常态化开展,弊端日益凸显。随着用电采集系统与智能电能表的普及应用,海量用户用电数据被广泛采集,使得利用数据挖掘方法实现低压台区户变关系辨识成为可能。

文献指出,具有电气连接的台区变压器与低压用户的电压波动情况具有相似规律,提出基于Pearson相关系数的户变关系辨识方法。

文献利用核模糊聚类算法将数据映射至高维特征空间完成用户聚类,并基于进化算法完成聚类参数优化,以提高户变关系辨识效果。为进一步提高户变关系辨识有效性,部分学者尝试在辨识分析前对量测数据进行预处理。

文献基于独立成分分析提取电压时序数据特征,并结合聚类算法完成户变关系辨识。

文献利用自适应分段聚合近似法提取电压变化特征,并基于改进DBsCAN聚类法识别户变关系异常用户。

综上所述,现有户变关系辨识方法多从整体角度衡量电压时序数据间的特征空间距离与形态相似度,对时序数据的局部特征细化不足,未实现多分辨率特征相似度分析。

针对上述问题,本文提出了一种基于多分辨率分析的配网台区户变关系辨识法。首先,利用EMD将电压量测数据分解为一系列特征互异的模态函数,并基于SE度量各子序列的复杂度,完成相关序列合并重组:然后,综合考虑各重组分量的多尺度特征,提出多分辨率距离和相似性测度全面度量电压时序数据的相似程度,并结合改进K-means算法完成户变关系辨识。算例分析结果表明,所提多分辨率辨识法综合考虑不同分量的细节特征,可实现户变关系有效辨识。

1基于EMD和SE的时序信号多分辨率分析

EMD是一种基于多分辨率思想的信号分解法,可自适应分解时间序列,解耦各特征尺度信息并降低原始时序数据的复杂度,以实现对原始数据内在规律、局部特征和变化趋势的细致刻画。考虑到EMD分解得到的各模态函数间存在相关性,采用SE度量各子序列的复杂度并完成相似序列合并重组,以强化同类序列的典型特征,并简化后续信号分析的计算规模。

1.1基于EMD的时序信号多分辨率分解

EMD是由学者Huang提出的一种基于多分辨率思想的信号分解法,可将原始信号自适应分解为一系列本征模态函数(IntrinsicModeFunction,IMF),细化表征原始信号在不同时间尺度的特性。

EMD具体步骤如下:

(1)寻找原始时序信号x(n)的所有极大值和极小值点。

(2)用曲线连接所有极大值点,经拟合构成信号的上包络u(n):用曲线连接所有极小值点,经拟合构成信号的下包络l(n),计算上下包络线的平均值为y(n):

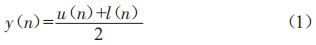
(3)令原始时序信号x(n)与平均值y(n)的差值为h(n):

(4)若h(n)不满足本征模态函数的要求,则视h(n)为新的信号x(n),转至步骤(1):若满足,则令h(n)为IMF分量。其中,第i个IMF分量ci(n)表示为:

(5)将原始时序信号x(n)与ci(n)差值的剩余分量视为新的信号x(n),并转至步骤(1),直至得到所有的分量。

由此,原始时序信号x(n)经EMD分解为K个IMF分量ci(n)和1个剩余分量r(n),则x(n)可表示为:

式中:K为IMF分量个数。

1.2基于SE的时序信号分量重构

EMD分解得到的模态函数数目较多且存在一定相关性,因此,为强化同类序列的典型特征并简化后续信号分析的计算规模,本文采用SE度量各子序列的复杂度,并将各子序列合并重构为趋势分量、细节分量和随机分量。

SE是由学者Richman提出的一种时序数据复杂度量化指标,其中,时序数据的样本嫡越小,表明时序数据的复杂度越小:时序数据的样本嫡越大,表明时序数据的复杂度越大。

SE具体步骤如下:

(1)将经EMD分解得到的分量序列:(n)构成一组m维的向量序列Zm(1),Zm(2),…,Zm(i),…,Zm(N-m＋1)。其中,Zm(i)={:(i),:(i＋1),…,:(i＋m-1)},1≤i≤N-m＋1,N为分量序列的数据点数。

(2)定义向量Zm(i)和Zm(j)间的距离为:

式中:1≤j≤N-m＋1且j≠i:0≤a≤m-1。

(3)设定相似容限1,统计向量Zm(i)和Zm(j)间距离小于1的个数与距离总数N-m的比值:

(4)求上述比值的平均值:

(5)将序列维度由m维改为m＋1维,重复步骤(1)~(4),计算得到Bm＋1(1)。

(6)当N为有限值时,样本嫡为:

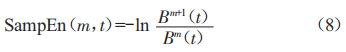
其中,m和1常取值2和0.2std,std为时序标准差。

若分量的样本嫡数值接近,则表示分量相关性高、融合性好,其产生信号新模式的概率基本一致,由此,依据嫡值数量级将各分量合并重构。其中,样本嫡为0.01数量级的分量合并为趋势分量,样本嫡为0.1数量级的分量合并为细节分量,样本嫡为1数量级的分量合并为随机分量。

式中:7为趋势分量:D为细节分量:R为随机分量。

子序列合并重构后,可强化同类序列的典型特征。其中,趋势分量7波动平缓,反映时间序列的整体趋势特征,具有较小的复杂度:细节分量D波动规律,反映时间序列的局部细节特征:随机分量R波动随机,反映时间序列的随机波动特征,具有较大的复杂度。

由此,基于多分辨率分析将原始时序信号分解为趋势、细节和随机三类分量,实现从不同层次细化信号多尺度特征。

2基于多分辨率分析的改进K-means聚类

2.1K-means聚类

K-means聚类算法利用距离测度度量样本间相似性,并将样本分为k个簇。其中,簇内样本间呈现较高的相似性,而不同簇样本间呈现较低的相似性。K-means算法流程如下:

(1)在样本集中随机选取k个初始聚类中心。

(2)计算所有样本与k个聚类中心的距离,将各样本归于距离最小的聚类中心所在簇。

(3)所有样本完成分簇后,令各簇内样本均值为新聚类中心,完成各聚类中心的更新:

式中:μi为簇Ci的聚类中心:x为样本。

(4)重复步骤(2)(3),直至误差函数收敛,则算法流程结束:

式中:E为聚类平方误差。

2.2基于多分辨率分析的改进K-means聚类

K-means聚类算法效果受初始聚类中心的影响大,随机设置初始聚类中心难以保证聚类结果的有效性与稳定性。此外,传统相似性测度仅从整体上度量样本间相似度,不具备多分辨率分析和多尺度特征刻画能力,难以体现样本局部细节特征的影响。针对上述问题,本文提出一种基于多分辨率分析的改进K-means聚类算法。

2.2.1初始聚类中心设置

本文研究低压用户与台变连接关系辨识,因此,可将聚类类别数设为待分析台变数,初始聚类中心设为各台变电压。

2.2.2多分辨率距离和相似性测度

令电压序列样本x的趋势分量、细节分量和随机分量分别为7x、Dx和Rx,则重构分量矩阵Mx可表示为:

式中:7jx、Djx和Rjx分别为7x、Dx和Rx的第j个元素。

综合考虑趋势分量、细节分量和随机分量的多尺度特征,提出多分辨率距离和多分辨率相似性测度以全面度量电压时间序列间的相似性。

2.2.2.1多分辨率距离测度

在计算样本x和N的距离时,综合考虑多分量特征计算样本间距离,得到样本x和N的多分辨率距离计算公式为:

式中:7jN、DjN和RjN分别为电压序列样本N的趋势分量、细节分量和随机分量的第j个元素。

2.2.2.2多分辨率相似性测度

基于矩阵相似度原理,综合考虑多分量特征计算样本间的相似度,得到样本x和N的多分辨率相似度计算公式为:

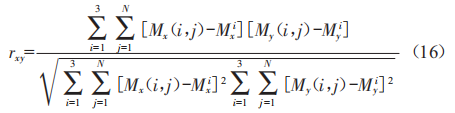
式中:yxN为样本x和N的多分辨率相似度:rx(i,j)和rN(i,j)分别为矩阵Mx和MN中i行j列的元素:rEQ * jc3 * hps11 oal(sup 3(和rEQ * jc3 * hps11 oal(sup 3(分别为矩阵Mx和MN中i行的平均值。

3算法流程

本文所提基于多分辨率分析的配网台区户变关系辨识法的算法流程如下:

步骤1:提取低压用户电能表电压数据和台变低压侧电压数据,将各电压序列样本值减去样本平均值,完成数据中心化处理。

步骤2:利用EMD提取电压序列数据的IMF分量和剩余分量,并基于SE重组得到趋势分量、细节分量和随机分量。

步骤3:初始化改进K-means聚类算法参数,聚类类别数k取待分析台变数,以各台变低压侧三相电压平均值为初始聚类中心。

步骤4:由式(l5)计算出各用户与k个聚类中心的电压时序数据多分辨率距离,将用户归类于距离最小的聚类中心所在簇。

步骤5:各用户完成类别划分后,令各簇样本的均值为新聚类中心,并利用EMD和SE分解重组得到新聚类中心的趋势分量、细节分量和随机分量。

步骤6:重复步骤4、5,直至误差函数收敛,则算法流程结束,完成户变关系辨识。

若采用多分辨率相似性测度,则将步骤4改为:由式(16)计算出各用户与k个聚类中心的电压时序数据多分辨率相似度,将用户归类于相似度最大的聚类中心所在簇。

4算例分析

本文选取广东某地2个台区的电压时序数据开展算例分析。台区A、B共有187个用户,用户电压数据采样频率为1h/点,选取某4周共28天数据进行台区户变关系辨识。

4.1台区户变关系辨识

经核查,台区A、B的户变关系信息正确。为了验证所提户变关系辨识法的计算效果,随机抽取2个台区共10个用户,将其台账档案调整至另一台区,并选择8种方法分别进行配网台区户变关系辨识,对比不同方法的辨识效果。其中,方法1和方法2为基于K-means算法的户变关系辨识法,分别采用欧氏距离和皮尔逊相关系数度量样本相似性:方法3和方法4为基于自动编码器和K-means算法的户变关系辨识法,分别采用欧氏距离和皮尔逊相关系数度量样本相似性:方法5和方法6为基于t分布随机近邻嵌入和K-means算法的户变关系辨识法,分别采用欧氏距离和皮尔逊相关系数度量样本相似性:方法7和方法8为基于多分辨率分析和K-means算法的户变关系辨识法,分别采用多分辨率距离和多分辨率相似度度量样本相似性。8种方法辨识结果如表1所示。

观察表1可知,方法3的辨识效果略优于方法1、2,方法4、6的辨识效果优于方法1、2,而方法7、8分别在基于距离和相似性测度的方法中辨识效果最优。结果表明,在分析前对电压时序数据进行特征预处理有助于提升户变关系辨识效果,且基于多分辨率分析的辨识法综合考虑不同分量的细节特征,可实现户变关系有效辨识。此外,由于欧氏距离关注时序数据在特征空间的绝对距离,未能有效反映时序数据曲线的形态与波动情况,因此,基于欧氏距离的户变关系辨识法计算效果整体劣于基于相似性测度的辨识法。

4.2数据长度对辨识效果的影响

为分析数据长度对户变关系辨识效果的影响,分别抽取计算长度为1天、3天、7天、14天和21天的时序数据,基于方法7和方法8开展配网台区户变关系辨识。不同时段的负荷特征不同,电压时序数据特征存在差异,因此,采用滑动窗形式重复进行户变关系辨识,统计分析数据长度对辨识效果的影响。

以数据长度7天为例说明计算方式,设定时间窗窗宽为7×24个数据点,以固定窗宽的滑动窗随机抽取时序数据进行户变关系辨识,重复50次统计辨识结果的平均值,结果如表2所示。

观察表2可知,方法7的辨识准确率随数据长度的增加呈现先增大、后减小的特点,而方法8的辨识准确率随数据长度的增加而提高。上述结果与高维空间距离度量失效有关,即多分辨率距离测度在高维空间无法准确度量样本距离。

由表1、表2可知,基于多分辨率相似度的户变关系辨识法计算效果优于基于多分辨率距离的户变关系辨识法。

5结论

(1)在户变关系分析前对电压时序数据进行特征预处理有助于提升辨识效果,且多分辨率辨识法综合考虑不同分量的细节特征,可实现户变关系有效辨识。

(2)基于多分辨率相似度的户变关系辨识法准确率随数据长度的增加而提高,而基于多分辨率距离的户变关系辨识法在高维空间的准确率降低。

(3)基于多分辨率相似度的户变关系辨识法计算效果优于基于多分辨率距离的户变关系辨识法。