经典控制理论的特点是以输入输出特性（主要是传递函数）为系统数学模型，采用频率响应法和根轨迹法这些图解分析方法，分析系统性能和设计控制装置。在实际操作中，确定控制参数也就是这两个步骤，一是确定系统的开环传递函数，二是整定传递函数，得到控制参数。

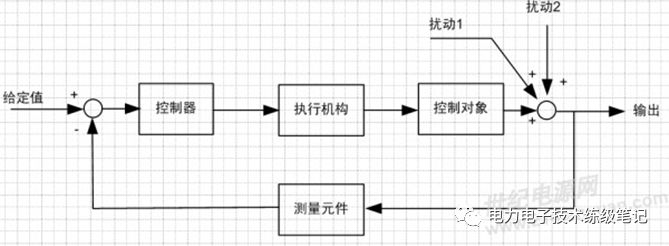
典型的反馈控制系统的框图

在反馈控制系统中，控制器对被控对象施加的控制作用是取自被控量（即输出量）的反馈信息，用来不断地修正被控量与给定值之间的偏差，从而实现对被控对象进行控制任务，这就是反馈控制的原理。

传递函数是在频域里面研究系统特性。频域里面，只需要幅值、频率和相位三个信息就能完全确定一个正弦信号。闭环传递函数比较复杂，特点不鲜明，同时所有的控制都是负反馈，所以只要开环传递函数确定了，闭环传递函数的特性也唯一了。

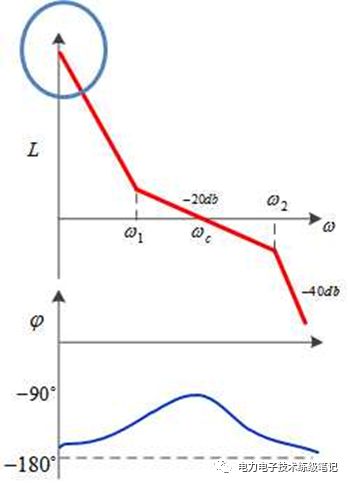
低频增益就是频率接近0时（直流分量），幅频特性的纵坐标值，如下图的蓝色圈所示。这个值决定了闭环系统的稳态精度。对于低频增益，我们希望越大越好，最好是无穷大。大家所熟知的积分环节，低频增益就是无穷大，用于消除稳态误差的。

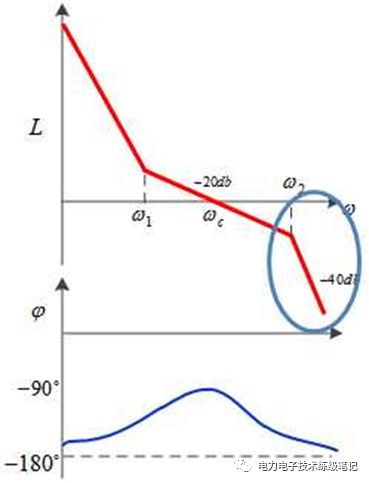
高频增益就是频率比较高的增益，如下图蓝框所示。这一段增益决定了系统抗干扰的能力。大家所熟知的干扰都含有高频成分。开环传递函数对高频的增益越低，衰减就越大，就不会对系统造成太大的扰动。所以我们希望高频段能快速降到0db一下，斜率越陡越好。

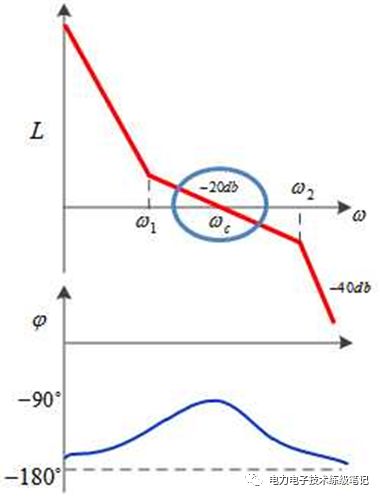
带宽就是开环幅频特性过0db所对应的频率Wc，也叫截止频率，如下图蓝框所示。截止频率越高，代表系统响应速度越快。截止频率以下，增益大于1，截止频率以上，增益小于1。也就是说，截止频率越高，系统能响应的信号频率也就越高，当然响应速度也就越快了。

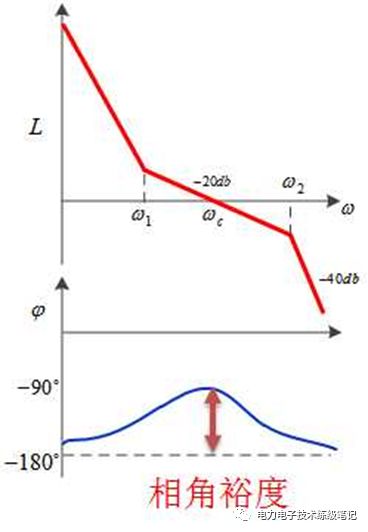
相角裕度指的是在截止频率处，相频特性对应的相角和-180度之间的距离。相角裕度决定了系统的稳定性。该值越大，系统越稳定。-180度是不稳定的点，这是因为-180度就相当于反向，乘以了-1，就把本身的负反馈变成了正反馈，系统就失稳了。或者可以这么理解闭环传递函数为G/(1+G)，可能使分母为零的点是不稳定点，G=-1，必须同时满足两个条件：开环传递函数的相位为-180°，同时|G|=1。

上面讲的都是用波特图分析系统稳定性的一些基本概念。大家可能更关心的是知道了开环传递函数后怎么计算PI参数？这个有很多种办法，下面介绍按照I型或者II型系统整定方法，需要指出的是，这只是工程中估计PI参数的一种，并非唯一方法。

首先说一下n型系统概念。对于开环传递函数，分母中有r个s，就是r型系统。0型系统，分母中没有s，低频增益是一个有限值，会有稳态误差。3型及以上系统很难稳定，因为分母的一个s就是90度响应，多个s相角裕度很快就没有了。所以常用的就是I型和II型系统。

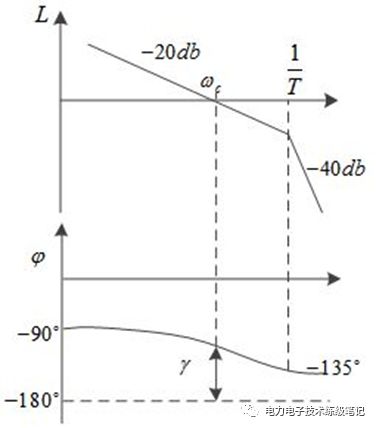
典型I型系统

I型系统结构简单，1+Ts为系统本身的一阶惯性环节，只需要确定K值即可。该系统的缺点是，对斜坡和加速输入跟踪性能差。从bode图上看，I型系统低频增益无穷大，没有稳态误差。高频以-40db斜率衰减，抗干扰能力强。截止频率越高，相角裕度越小；截止频率越低，相角裕度越大。

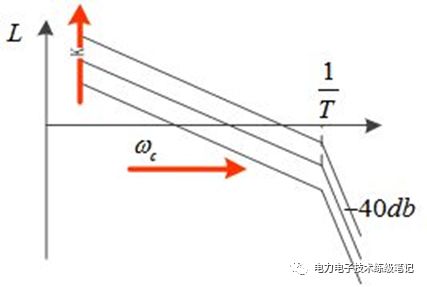
随着K增大，截止频率增大，增加了快速性；但降低了相角裕度和抗扰性。在配置中，通常取KT=0.5，来权衡快速性和稳定性。

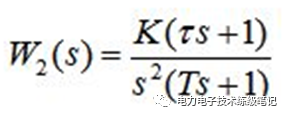
典型II型系统

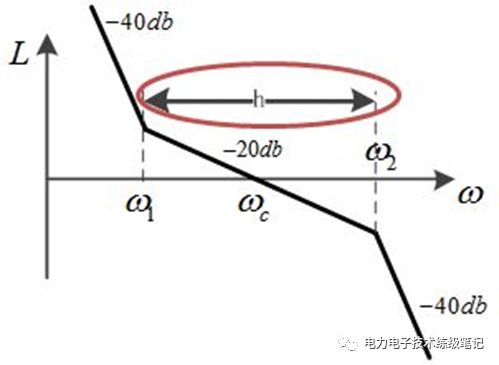
II型系统需要确定分子的两个参数K和τ，分母的1+Ts为系统的一阶惯性环节。II型系统对斜坡和加速输入能无静差跟踪。是电力电子控制中最常用的。K和τ有众多种组合，怎么来合理的确定它们呢？前人们针对II型系统有个中频带宽的概念，

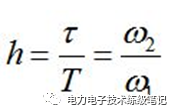
确定了中频宽h，就确定了τ，再改变K使得幅频特性上下平移，改变ωc。

学者们发现，对于确定的h，存在一个确定的K，使得闭环幅频特性峰值最小。K和h的关系为：

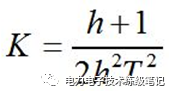
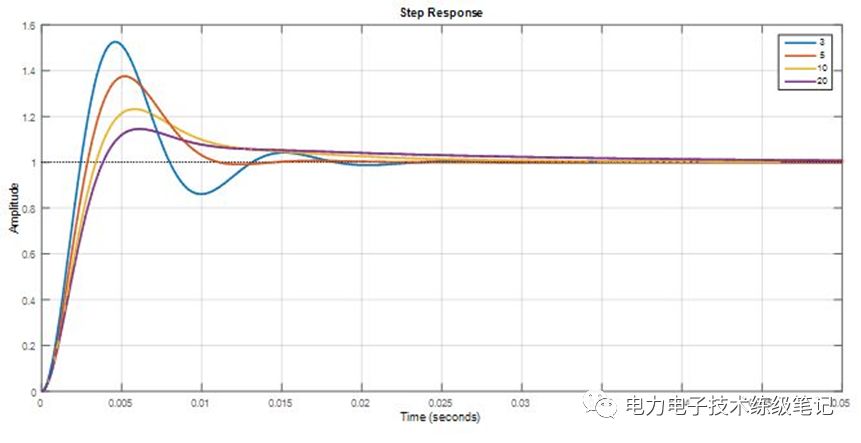
所以我们的工作就剩下，选择合适的h就可以了。不同的h有什么影响呢？如下图所示，h越小，阶跃响应越快，但震荡越多，超调越大；h越大，阶跃响应越慢，但震荡越小，超调越小。大家可以根据自己的需要，选择不同的h来配置II型系统。