摄像机标定的目的：三维重建

空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数，为了得到这些参数而进行的实验与计算的过程称为摄像机标定。

在标定过程中通常要利用数学方法对从数字图像中获得的数据进行处理。通过这些数学处理，可以得到摄像机的内部和外部参数。

一、成像几何模型

1.世界坐标系

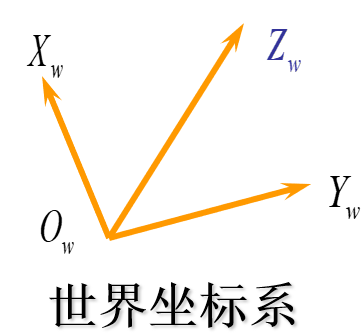
2.摄像机坐标系

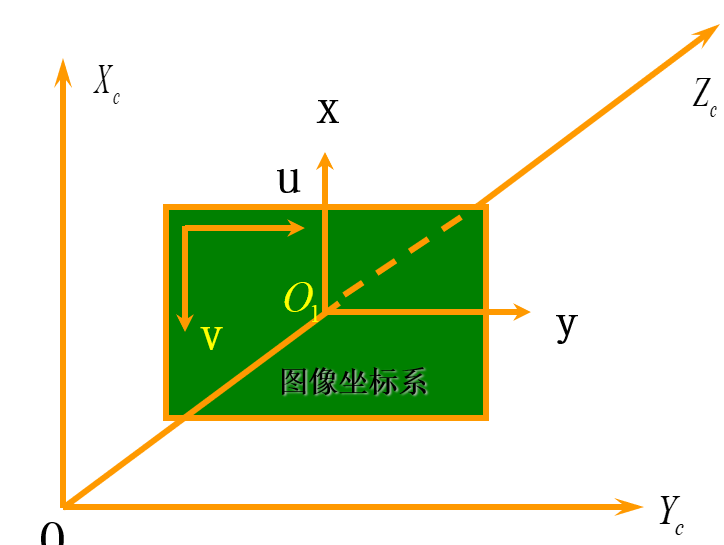
3.图像坐标系

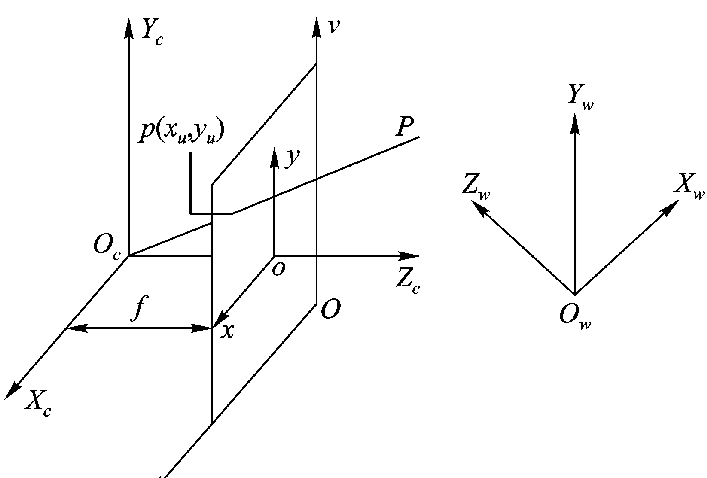
M1只与摄像机内部结构有关，称为摄像机内部参数；M2只与摄像机相对于世界坐标系的方位有关，称为摄像机外部参数；X为空间点在世界坐标系下的齐次坐标，M为矩阵，称为透视变换矩阵。

4.空间点与像点的非线性关系分析

由于摄像机的光学成像系统与理论模型之间的差异，二维图像存在着不同程度的非线性变形，目标像点与理论成像点相比存在着多种类型的几何畸变.

径向畸变主要是由镜头形状缺陷造成的，是关于摄像机镜头的主光轴对称的。

正向畸变是枕形畸变，负向畸变是桶形畸变，其数学模型为：

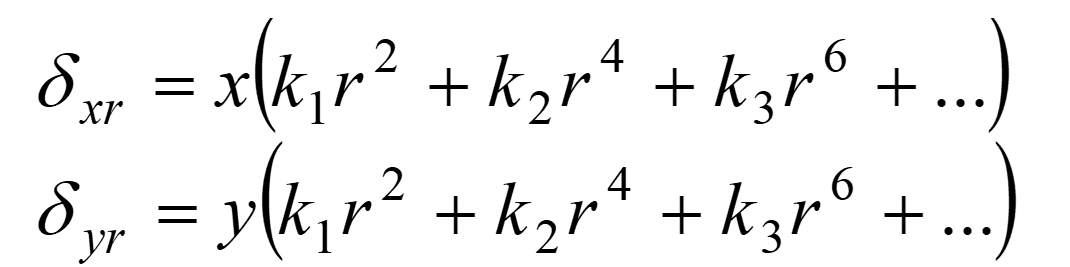
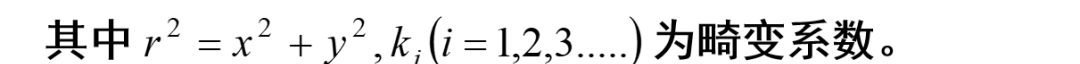
偏心畸变主要是由光学系统光心与几何中心不一致造成的，即各透镜的光轴中心不能严格共线。

这类畸变既含有径向畸变，又含有切向畸变。

切向畸变的数学模型为：

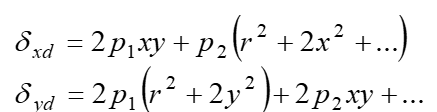
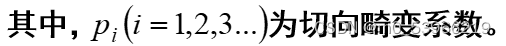
薄棱镜畸变是由于镜头设计、制造缺陷或加工安装误差所造成的，如镜头与摄像机像面有很小的倾角等。

这类畸变相当于在光学系统中附加了一个薄棱镜，不仅会引起径向偏差，而且引起切向误差。

其数学模型为：

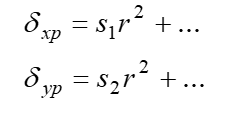
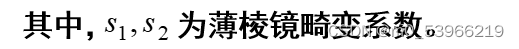
二、典型标定方法

1.传统摄像机标定方法

优点：可以使用于任意的摄像机模型，标定精度高。

不足：标定过程复杂，需要高精度的已知结构信息。在实际应用中很多情况下无法使用标定块。

2.摄像机自标定方法

特点：仅依靠多幅图像之间的对应关系进行标定。

优点：仅需要建立图像之间的对应，灵活性强，潜在应用范围广。

不足：非线性标定，鲁棒性不高。

3.传统的摄像机标定方法

利用已知的景物结构信息。常用到标定块。

•利用最优化算法的标定方法

•利用摄像机变换矩阵的标定方法

•两步法

•双平面标定法

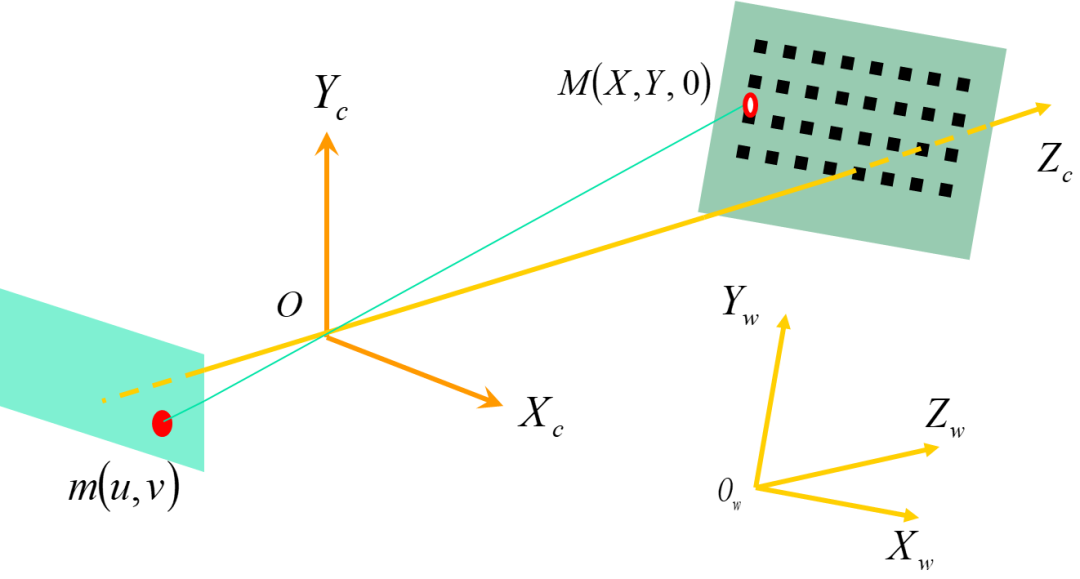
基本原理：

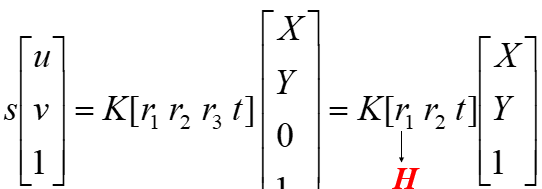
其中，K为摄像机的内参数矩阵。由于摄像机有5个未知内参数，所以当所摄取得的图象数目大于等于3时，就可以线性唯一求解出K。

4.摄像机自标定方法

利用本质矩阵和基本矩阵的摄像机标定方法；利用主动系统控制摄像机作特定运动的自标定方法（主动视觉标定方法）。

5.基于平面单应矩阵的正交运动方法原理

t(1)、t(2)为摄像机一组正交的平移运动，两个单应矩阵：

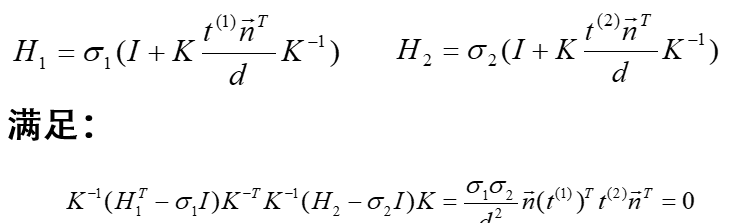
五组两正交运动可完全求解5个内参数。