在昨天,通过扫频的方法分别测量了两个动圈式扬声器在不同频率下的阻抗。 两个扬声器中小型扬声器, 直流阻抗为4欧姆。 另外一个是大型低频扬声器,直流电阻为8欧姆。 前天,通过施加阶跃电压测量了扬声器单位冲激响应信号。 通常情况下, 扬声器可以看成一个近似线性时不变系统。 它的单位冲激响应信号的傅里叶变换, 应该对应它的频率特性。 下面就利用实际测量的数据, 来分析它们之间的关系。
本文引用地址:01 冲激响应
一、前言
在昨天,通过扫频的方法分别测量了两个动圈式扬声器在不同频率下的阻抗。 两个扬声器中小型扬声器, 直流阻抗为4欧姆。 另外一个是大型低频扬声器,直流电阻为8欧姆。 前天,通过施加阶跃电压测量了扬声器单位冲激响应信号。 通常情况下, 扬声器可以看成一个近似线性时不变系统。 它的单位冲激响应信号的傅里叶变换, 应该对应它的频率特性。 下面就利用实际测量的数据, 来分析它们之间的关系。
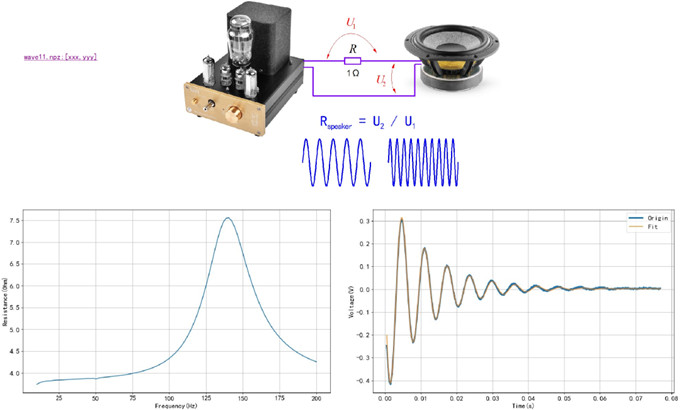
图1.1.1 扬声器的特性与敲击振荡信号
二、分析结果
1、小型扬声器
这里小型扬声器单位冲激响应数据, 利用曲线拟合可以获得该型号的衰减振荡信号参数。 通过参数C可以计算出 信号的自由振荡频率, 频率数值为 158.31Hz。
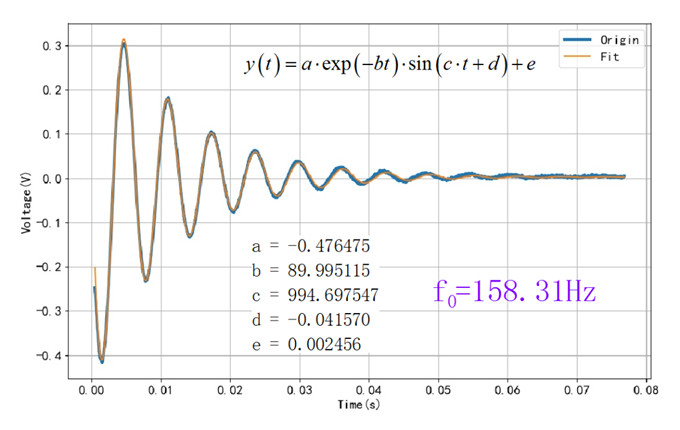
图1.2.1 单位冲激响应波形建模
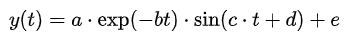
利用扫频的方式测量扬声器的特性, 对应阻抗最大值的频率 是扬声器的谐振频率, 它的数值为140.51Hz。 相比于单位冲激响应的振荡频率来说, 扬声器的谐振频率要小。
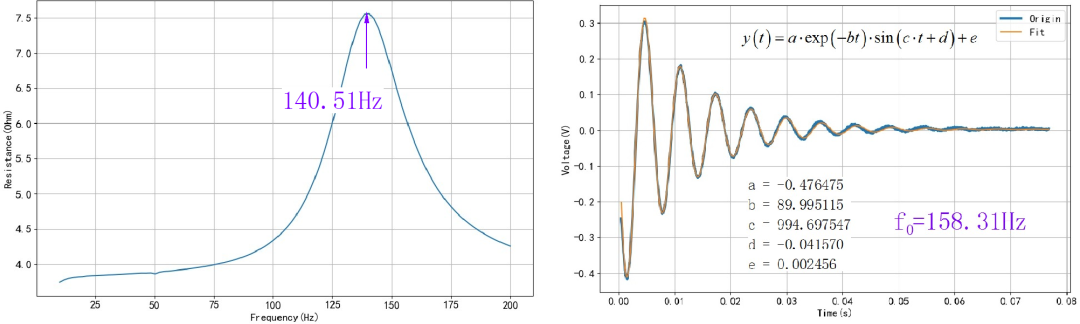
图1.2.2 阻抗谐振频率与单位冲激响应振荡频率
我们知道系统的单位冲激响应的傅里叶变换对应着系统的幅频特性。 利用信号的数学表达式, 求取信号的FFT。绘制出结果的幅度谱。 可以看到它与前面通过扫频获得扬声器的阻抗曲线形状非常接近。 虽然形状很接近, 但是峰值对应的频率却相差比较大。 究其原因,有可能是测量扬声器的运动的单位冲激响应是在外部不连接放大器的情况下测量的, 而扬声器扫频测量的时候则是在连接有功放情况下测量的, 此时有可能线圈感应与外界驱动电路形成回路产生阻尼,使得谐振频率降低了。
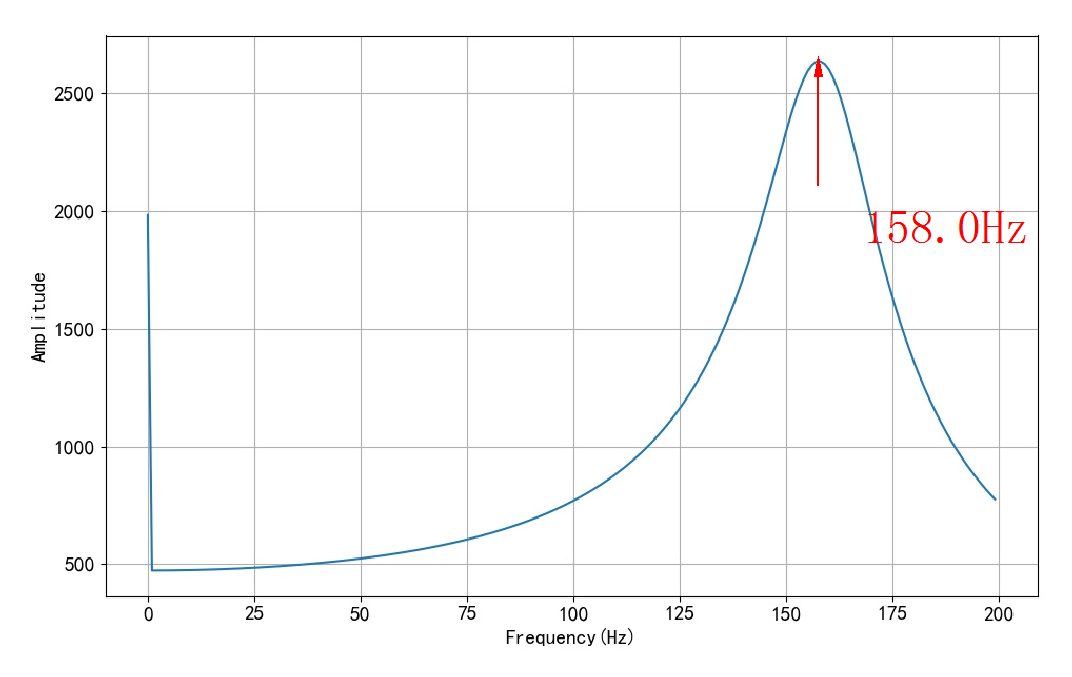
图1.2.3 冲激响应信号的傅里叶变换幅度谱
2、大型扬声器
这是大型扬声器通过扫频方式测量得到的特性。 谐振频率为48.34Hz。 通过施加阶跃电压信号,可以测量得到扬声器的单位冲激响应信号。 求取该信号的衰减指数函数参数。 通过频率参数C, 可以计算出振荡频率为47.85Hz。 这就与扬声器的阻抗峰值对应的频率相差不多了。 这应该是由于大型扬声器纸盆质量比较大, 线圈阻尼对谐振频率的影响不大。

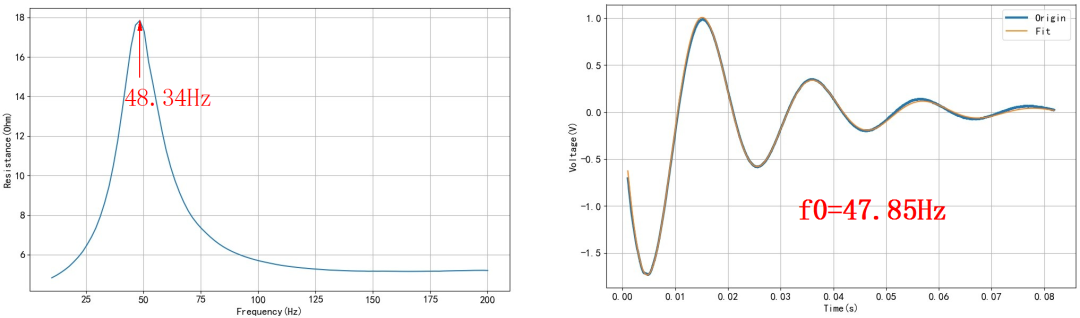
图1.2.4 大型扬声器阻抗特性与冲击振荡信号
总结
本文对两款扬声器的与它的阻抗频率特性进行分析, 对于大型扬声器来说,从单位冲激响应信号所得到的振荡频率与最大阻抗对应的谐振频率是相同的。 对于小型扬声器由于受到线圈的阻尼,阻抗最大值对应的频率小于敲击对应的振荡频率。
参考资料
[1]扬声器的单位冲激响应信号建模: https://zhuoqing.blog.csdn.net/article/details/129278199
[2]如何获得扬声器完美的单位冲激响应?: https://zhuoqing.blog.csdn.net/article/details/129326598
[3]扬声器的阻抗频率特性: https://zhuoqing.blog.csdn.net/article/details/129337393










