摘要
本设计是基于STM32F4的四轴航拍平台。以STM32F407为控制核心,四轴飞行器为载体,辅以云台的航拍系统。硬件上由飞控电路,电源管理,通信模块,动力系统,机架,云台伺服系统组成。算法上采用简洁稳定的四元数加互补滤波作为姿态解算算法,PID作为控制器,实现飞行,云台增稳等功能。具有灵活轻盈,延展性,适应性强好等特点。
引言
四轴飞行器是一种利用四个旋翼作为飞行引擎来进行空中飞行的飞行器。进入20世纪以来,电子技术飞速发展四轴飞行器开始走向小型化,并融入了人工智能,使其发展趋于无人机,智能机器人。
四轴飞行器不但实现了直升机的垂直升降的飞行性能,同时也在一定程度上降低了飞行器机械结构的设计难度。四轴飞行器的平衡控制系统由各类惯性传感器组成。在制作过程中,对整体机身的中心、对称性以及电机性能要求较低,这也正是制作四轴飞行器的优势所在,而且相较于固定翼飞机,四轴也有着可垂直起降,机动性好,易维护等优点。
在实际应用方面,四轴飞行器可以在复杂、危险的环境下可以完成特定的飞行任务,也可以用于监控交通,环境等。比如,在四轴飞行器上安装甲烷等有害气体的检测装置,则可以在高空定点地检测有害气体;进入辐射区检查核设施;做军事侦察;甚至搬运材料,搭建房屋等等。本设计利用四轴搭载云台实现航拍任务,当然经过改装也可以执行其他任务。
本设计主要研究了四轴飞行器的姿态结算和飞行控制,并设计制作了一架四轴飞行器,对关键传感器做了标定,并利用用matlab分析数据,设计算法,还进行了单通道平衡试验调试,进行试飞实验取得了一定的效果。
2.系统方案
本设计采用STM32F4作为核心处理器,该处理器内核架构 ARM Cortex-M4,具有高性能、低成本、低功耗等特点。
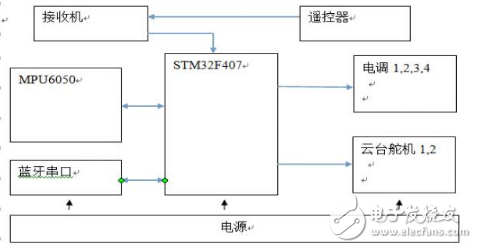
主控板包括传感器MPU6050电路模块、无线蓝牙模块、电机启动模块,电源管理模块等;遥控使用商品遥控及接收机。控制芯片捕获接收机的PPM命令信号,传感器与控制芯片之间采用IIC总线连接,MCU与电调之间用PWM传递控制信号。
软件算法才用基于四元数的互补滤波解算姿态叫,控制算法才用经典PID控制器控制云台舵机和四轴电机。如图2-1为本设计总体框图。
3.系统硬件设计
针对前面提出的整体设计方案,本设计采取模块化策略,将各个功能部分开来设计,最后组合起来。
3.1 电源管理模块
四轴飞行器要求整体设计质量较轻,体积较小,因此在电池的选取方面,采用体积小、质量轻、容量大的锂电池供电最合适。系统的核心芯片为STM32F103,常用工作电压为3.3V,同时惯性测量传感器,蓝牙通信模块的常规供电电压也为3.3V,锂电池的电压为11.4V,要使系统正常工作,需要将11.4V的锂电池电压稳压到3.3V。常用的78系列稳压芯片已不再适用,必须选择性能更好的稳压芯片。
经综合考虑,本电路采用LM1117-3.3和LM2940-5电源部分的核心芯片。电池电源经过LM2940-5降到5V后在输入LM1117-3.3稳压为3.3V。由于电机部分电流较大,故在飞控电路部分加入了过流保护,使用500mA的保险丝。电路图如下。
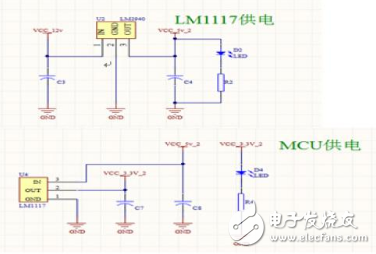
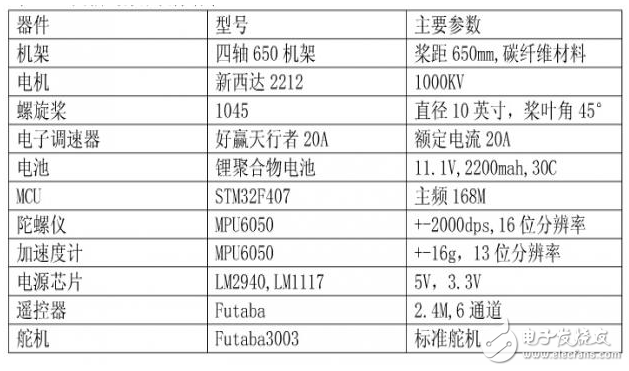
表3-1 四轴飞行器硬件清单
4.系统软件设计
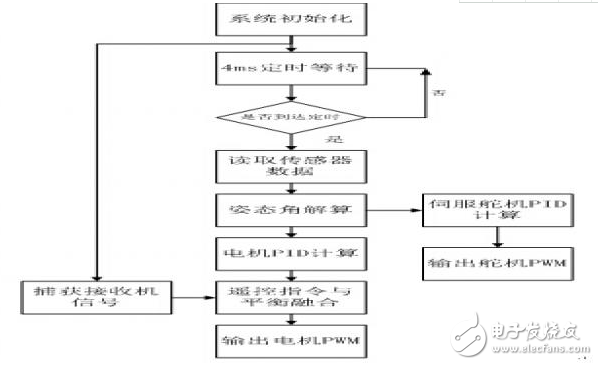
软件设计上由控制核心STM32F4读取传感器信息,解算姿态角,以姿态角为被控制量融合遥控信息后,输出到四个电机及两个舵机以完成四轴飞行控制和云台的稳定补偿。下图是软件流程:
4.1.四元素计算姿态角的实现
根据前面给出的姿态解算方程与四元数,即可得到姿态计算系统的计算原理如下图(4-1)
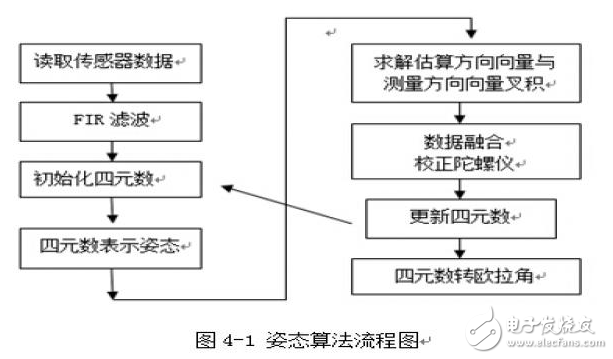
本设计基于互补滤波的思想上完成的四元素算法,其核心思路为利用加速度测得的重力向量与估计姿态得到重力向量的误差来矫正陀螺仪积分误差,然后利用矫正后的陀螺仪积分得到姿态角。
首先不妨设处理后的加速度数据为:ax,ay,az,单位m/s^2。加速度计的向量为 (ax,ay,az)陀螺仪数据为:gx,gy,gz,单位rad/s。陀螺仪向量 (gx,gy,gz),由式(4-5)可得由载体到导航坐标系的四元数形式转换矩阵为:
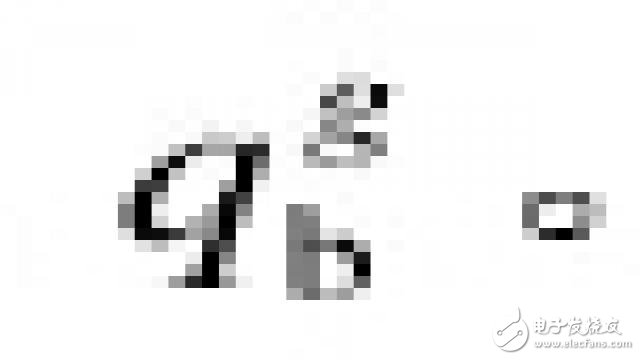
根据余弦矩阵和欧拉角的定义,地理坐标系的重力向量,转到机体坐标系,是 中的第三列的三个元素,即
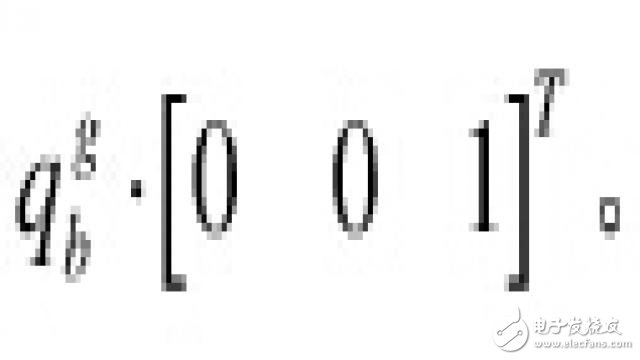
。所以加速的向量与估计重力向量叉积:
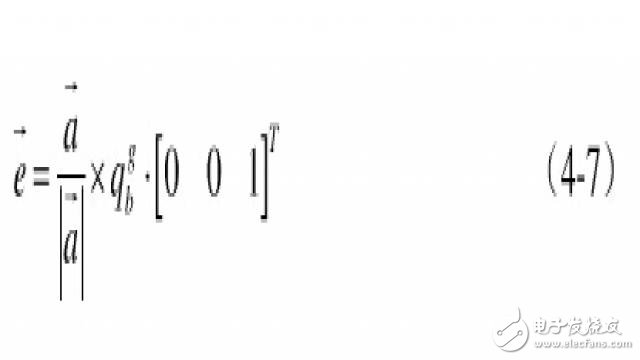
然后利用向量的叉积, 可视为误差向量,这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。用上面得到的结果校正陀螺仪:
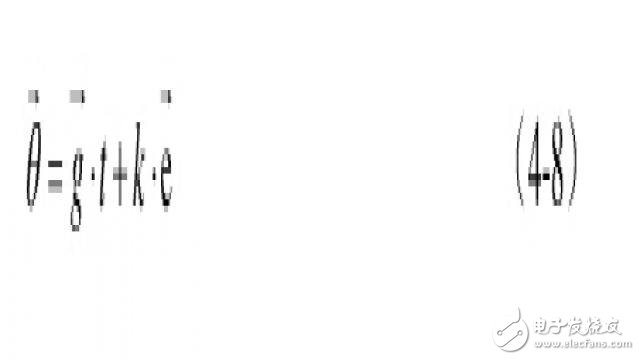
此处k为一个常量系数。
再利用二阶毕卡法解四元数微分方程(4-6),更新四元数为下一次计算做准备。毕卡二阶算法为:
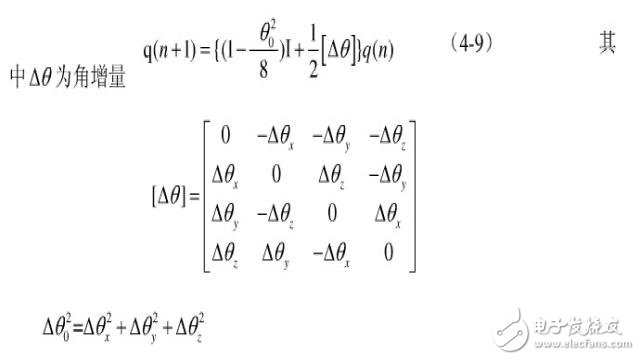
最后将四元数转变为欧拉角:

数据流程图如下:
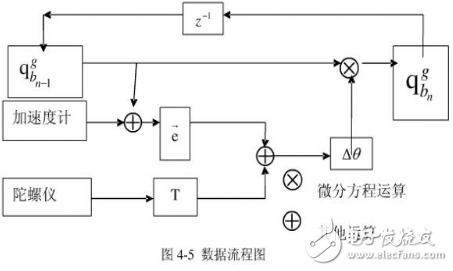
通过以上算法我成功得出了飞行器的姿态角,在开启电机的情况下,角度误差在+/-2°以内,满足了控制要求。姿态计算效果如下图所示,其中红色和蓝色是直接由加速度计算出的俯仰角和横滚角,青色和黄色为姿态结算后的俯仰角和横滚角。由图中数据可看出,解算的姿态角不仅能即时的反应角度变化切曲线平滑,说明姿态解算算法有效。
4.2.控制设计
由于四轴飞行器独特的机械结构,即结构上的对称设计,使得四轴在俯仰角的控制欲横滚角的控制上有这近乎相同的控制特性,且两者相对独立。四轴飞行器的俯仰,横滚,偏航,升降可以通过四个输入量来控制。通过设定一个期望角度,调整电机转速,使得测得的姿态角稳定在期望角。控制律的设计主要采用是闭环控制。以姿态角做为被控制量,采用经典的PID控制算法。
四轴飞行器系统是一个时变且非线性的系统,采用传统PID算法的单一的反馈控制会使系统存在不同程度的超调和振荡现象,无法得到理想的控制效果。本文将前馈控制引入到了四轴飞行器系统的控制中,有效地改善了系统的实时性,提高了系统的反应速度;并且根据四轴飞行器系统的特点,对数字PID算法进行了改进,引入了微分先行环节,改善了系统的动态特性;使得控制器能够更好地适应四轴飞行器系统的实际情况。
在姿态角的控制中,本设计将控制器捕获到的遥控器信号转换为一个角度,作为期望角,与解算出来的测量角作差,得到偏差error。将error乘以一个比例系数kp。在只有kp作用下,系统会有静差所以考虑利用积分ki控制消除稳态误差。但积分控制会降低系统的动态性能,甚至造成闭环系统不稳定,因此要对积分进行限幅,防止积分过大。
对于微分,如果采用传统的D方法,在人为操纵四轴时会产生输入的设定值变化频繁且幅度较大,从而造成系统的振荡。对人为控制十分不利,为了解决设定值的频繁变化给系统带来的不良影响,本文在姿态角控制上引入了微分先行PID算法,其特点是只对输出量进行微分,即只对陀螺仪角速度测量值进行微分,而不对姿态角的设定值进行微分。这样,在设定值发生变化时,输出量并不会改变,而被控量的变化相对是比较缓和的,这就很好地避免了设定值的频繁变化给系统造成的振荡,明显地改善了系统的动态性能。控制周期定为4ms,姿态控制系统示意图如下:
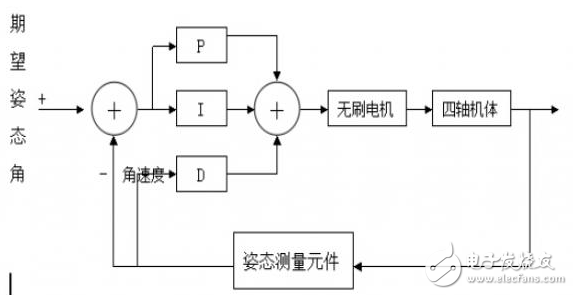
图5-1姿态控制系统示意图
通过前面一章的介绍我们已经的达到了俯仰,横滚,航向三个控制量,然后将它们分别输入三个独立的如上图所示的PID控制器,我们可以得到三个PID输出:pid_roll,pid_pitch,pid_yaw将这三个输出量做简单的线性运算输出给电机。部分代码如下:
#define PIDMIX(X,Y,Z) Motor_Thr + pid_pitch* Y+ pid_roll*X + pid_yaw*Z
MOTOR1=MOTORLimit(PIDMIX(+1,+1,-1)); //REAR_R 后右电机
MOTOR2=MOTORLimit(PIDMIX(-1,-1,-1)); //FRONT_R 前右电机
MOTOR3=MOTORLimit(PIDMIX(-1,+1,+1)); //REAR_L 后左电机
MOTOR4=MOTORLimit(PIDMIX(+1,-1,+1)); //FRONT_L 前左电机
4.3. PID参数调节
PID参数的整定是PID控制的关键环节,直接影响到控制的效果。故一个PID设计的好不好往往要看其参数能否调节好,本设计的PID参数调节采用凑试法。凑试法是通过实际的闭环系统,通过观察系统的响应曲线,在本设计中通过观察被调量,PID输出,设定值三条曲线,判断出kp,ki,kd对系统响应的影响,反复尝试,最终达到满意响应,从而达到确定控制参数的kp,ki,kd的目的。在参数调节过程总遵循以下原则[17]:
(1)在输出不振荡时,增大比例增益P。
(2)在输出不振荡时,减小积分时间常数Ti。
(3)在输出不振荡时,增大微分时间常数Td。
(4)一般步骤:
a.确定比例增益P
确定比例增益P时,首先去掉PID的积分项和微分项,一般是令Ti=0、Td=0(具体见PID的参数设定说明),使PID为纯比例调节。输入设定为系统允许的最大值的60%~70%,由0逐渐加大比例增益P,直至系统出现振荡;再反过来,从此时的比例增益P逐渐减小,直至系统振荡消失,记录此时的比例增益P,设定PID的比例增益P为当前值的60%~70%。比例增益P调试完成。
b.确定积分时间常数Ti
比例增益P确定后,设定一个较大的积分时间常数Ti的初值,然后逐渐减小Ti,直至系统出现振荡,之后在反过来,逐渐加大Ti,直至系统振荡消失。记录此时的 Ti,设定PID的积分时间常数Ti为当前值的150%~180%。积分时间常数Ti调试完成。
c.确定积分时间常数Td
积分时间常数Td一般不用设定,为0即可。若要设定,与确定 P和Ti的方法相同,取不振荡时的30%。
d.系统空载、带载联调,再对PID参数进行微调,直至满足要求。
(5)最终调试好的标准应该是,PID输出曲线在有一个阶跃响应来是,响应一大一小两个波,小波是大波的四分之一。
四轴飞行器的PID整定,我们首先四轴固定在单轴平衡平台上,让飞行器完成单轴平衡,主要观察姿态角的(1)稳定性,能否平衡在期望角度;(2)响应性,当操纵命令改变时,四轴能否即时的响应期望的变化;(3)操纵性,由操纵员感受四轴的姿态是否已与操纵,会不会产生响应过冲。
在参数调整时,先调P,将I,D给0,先给一个小值P1,如果飞行器不能稳定在一个角度,则P1给小了,下一次给一个较大值P2,如果飞行器产生震荡则证明P2给大了,那么合适的P在P1-P2之间,反复试验几次可找到P震荡的临界点P0,然后保持P0不变按照调P的方法来调D,D是用来消除误差的,当抖动差不多被消除时,此时我们有较合适的P0,D0,在这两个值附近再试几组参数,观察效果得到最优参数。调好P,D后此时四轴的稳定状态与期望状态间也学会有静差,接下来加入I,参数有小到大,当静差差不多被消除时,我们再对P,I,D三组参数在小范围内联调。最后确定恰当的积分限幅值,完成整个PID参数的整定。
5.系统创新
采用STM32F407这样一款高性能芯片作为控制核心,计算快速,扩展空间大。
云台飞控一体化设计,既能完成飞行任务也能实现云台稳定。
姿态算法采用基于四元数的互补滤波,姿态角无奇点,比起卡尔曼李春波等高端算法有着计算量小的特点且能投入使用,大大节约了cpu计算时间,也降低了对cpu的性能要求。
利用四轴作为云台载体有着灵活机动,可让摄像头获得比较好的视野,且云台能消除四轴机体抖动。
方便改装用于执行其他任务。
6.评测与结论
6.1.四轴飞行器的调试
6.1.1电源调试
将电路板焊接完成后,为电路板供电,用万用表测得个供电芯片电压如下
表6-1各电源芯片电压值

由表中数据可知电源管理部分可满足系统供电要求。
6.1.2 姿态角调试
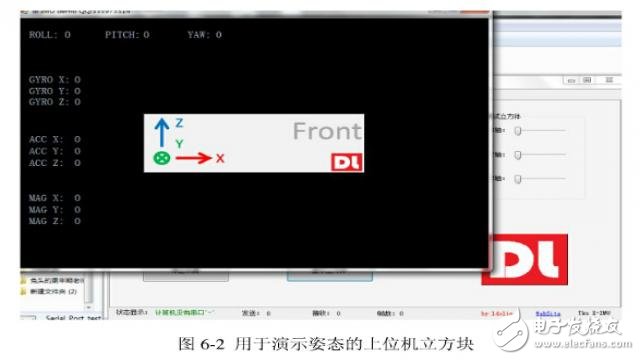
在完成控制器底层的硬件驱动后,开始姿态角算法的调试。利用蓝牙模块将解算出的姿态角数据发回上位机,摇动四轴机体,观察上位机数据曲线与姿态演示立方块。
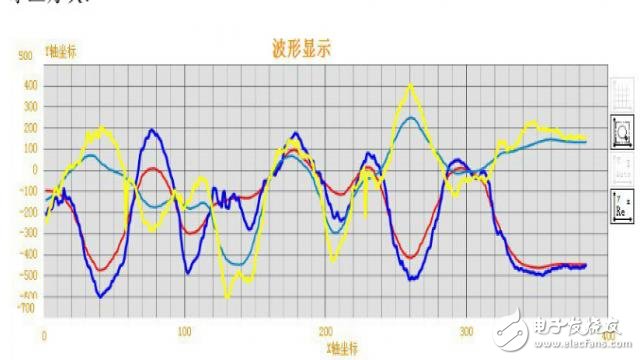
图6-1 姿态角数据对比曲线
图6-1中黄色和蓝色为直接由加速度计算出的俯仰与横滚角,红色和青色为姿态解算后的姿态角,可明显看出直接由加速度计算出的姿态角噪声大,不平滑,不能真实反映姿态角的变化。而由四元数算法解算后的姿态角反应快,噪声小,足以满足控制要求。光观察曲线并不直观,还可以观察上位机中的立方块,当小立方块的姿态与四轴机体能够保持一致变化时说明姿态解算良好。通过以上手段可知姿态角解算满足需求。
6.1.3 控制电机调试
在第五章,已经针对四轴飞行器进行了PID的控制设计,但为了得到实际使用的PID控制参数我们还需要通过反复试验来整定出最优参数。为了方便参数的调试,在本设计过程中才用了先调平衡一个方向,再调另一个方向,最后联达到平衡的效果。为此设计了如下图所示试试验平台:
图6-3 四轴单轴平衡试验
在调试过程中,为了避免频繁的下载程序带来的不变,采用串口蓝牙发送参数的做法,大大提高了调试效率。当俯仰与横滚两个轴都能够独立的平衡时,可以脱离单轴平台开始在空中进行航向角的稳定性调试。
6.2.四轴飞行器的试飞
当前面的各项调试都完成了之后,就准备要进行试飞实验。飞行试验是对控制系统的功能和技术指标进行验证的最终手段,也是衡量四轴设计是否成功的重要标志。
试飞前要确保系统各部分工作正常,稳定。检查各个接口连接是否正确,各部件安装是否牢固,电池电量是否充足。打开电源前检查遥控器油门是否在最低位置,起飞前先轻推油门确保电机工作正常。一切准备就绪,即可进行试飞。将四种飞行器放在水平地面上,开始启动姿态初始化程序,听到电调提示音后,缓慢增加油门,螺旋桨转速上升,将飞机拉离地面。由实际情况可看出当姿态发生倾斜时,姿态解算及PID控制能够及时调整电机转速,稳定飞行姿态。飞行器还能根据遥控指令的变化完成相应的动作。本此设计的四轴飞行器可实现垂直升降的要求,能保持姿态的稳定,机体晃动小,在微风的干扰下能够自动调整姿态,确保平稳飞行,且系统响应快,续航时间大概在8分钟。因此本次的设计是有效的。
附录
部分代码
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
{
static float q0 = 1.0f, q1 = 0.0f, q2 = 0.0f, q3 = 0.0f;
float delta_2=0;
const static float FACTOR = 0.002;
float norm=0.0f;
float vx, vy, vz;
float ex, ey, ez;
float q0q0 = q0*q0;
float q0q1 = q0*q1;
float q0q2 = q0*q2;
float q1q1 = q1*q1;
float q1q3 = q1*q3;
float q2q2 = q2*q2;
float q2q3 = q2*q3;
float q3q3 = q3*q3;
norm = sqrt(ax*ax + ay*ay +az*az); // 测量正常化 把加速度计的三维向量转成单位向量。
ax = ax /norm;
ay = ay / norm;
az = az / norm;
vx = 2*(q1q3 - q0q2); // 估计方向的重力
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
ex = (ay*vz - az*vy);
ey = (az*vx - ax*vz);
ez = (ax*vy - ay*vx);
halfT=0.002;
gx = gx + ex*FACTOR/halfT; //校正陀螺仪测量值 用叉积误差来做PI修正陀螺零偏
gy = gy + ey*FACTOR/halfT;
gz = gz + ez*FACTOR/halfT;
delta_2=(2*halfT*gx)*(2*halfT*gx)+(2*halfT*gy)*(2*halfT*gy)+(2*halfT*gz)*(2*halfT*gz);
q0 = (1-delta_2/8)*q0 + (-q1*gx - q2*gy - q3*gz)*halfT; // 整合四元数率 四元数微分方程 四元数更新算法,二阶毕卡法
q1 = (1-delta_2/8)*q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = (1-delta_2/8)*q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = (1-delta_2/8)*q3 + (q0*gz + q1*gy - q2*gx)*halfT;
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3); // 正常化四元
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
//转换为欧拉角
Q_ANGLE.Pitch = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch
Q_ANGLE.Roll = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll
Q_ANGLE.Yaw = -atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3 * q3 + 1)* 57.3; // yaw
}
相关文章

















 技术咨询
技术咨询 代买器件
代买器件 商务客服
商务客服 研发客服
研发客服