01 先修知识

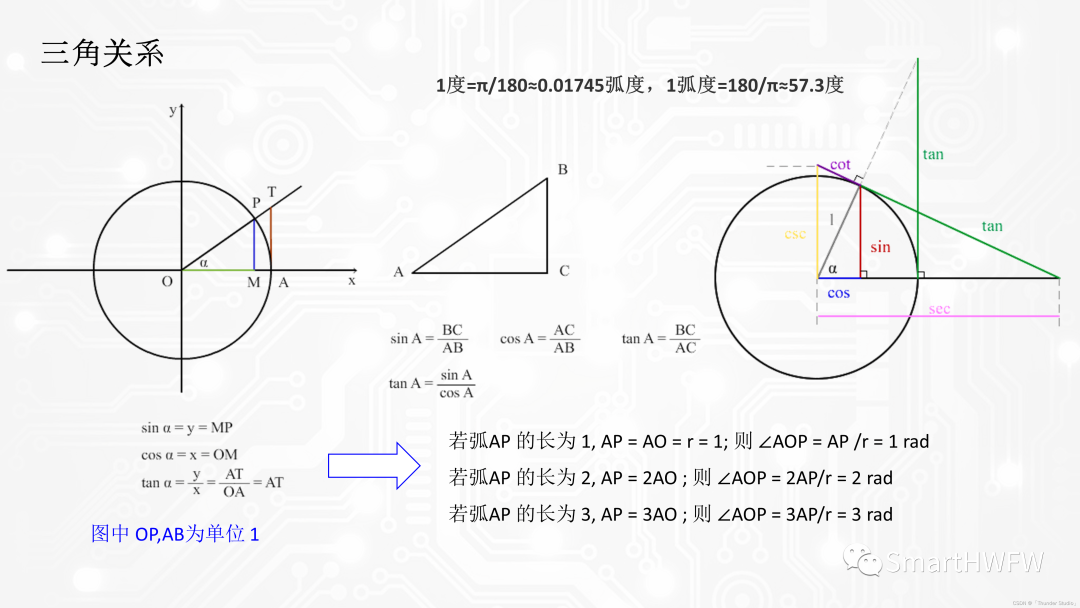
02 原理(单轴为例)

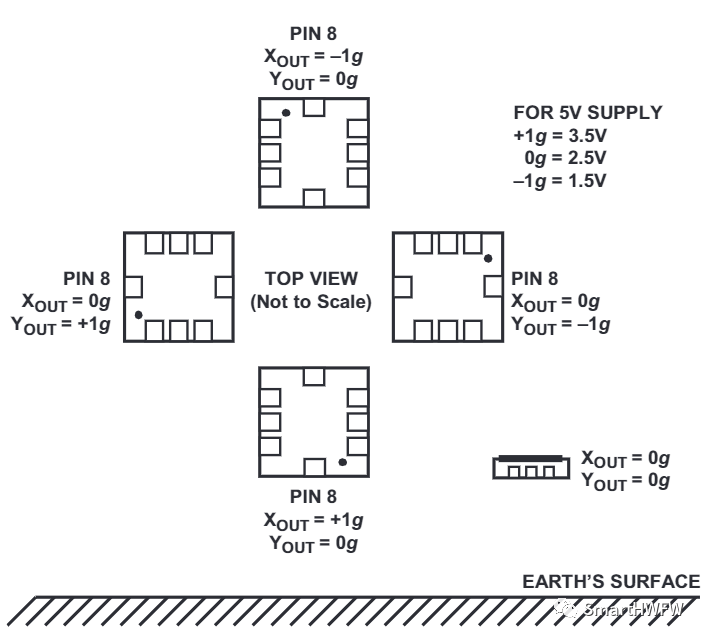
首先我们要知道的是：当目标轴(本例中为X轴)与地球表面平行时,传感器处于 0g 场。顺时针或逆时针旋转90° 将分别产生+1g或−1g 场。下图是传感器不同方向的布局与对应的输出 g 值：

单轴倾斜

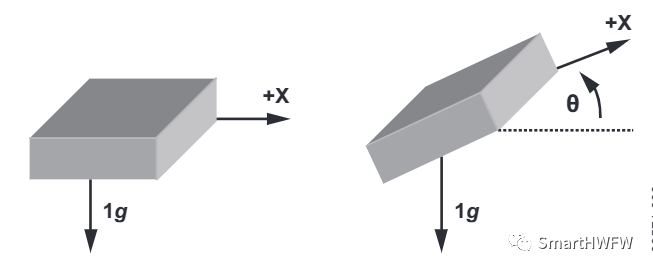
当X轴发生倾斜后，根据三角恒等式，X轴上的重力矢量投影会产生输出加速度,大小等于加速度计 X轴和水平面之间夹角的正弦值。水平面通常是与重力矢量正交的平面。当重力为理想值 1g 时,输出加速度为:

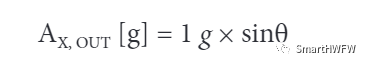
利用反正弦函数可以将加速度转换成倾斜角。

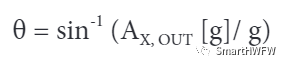
其中,倾斜角θ单位为弧度。

双轴倾斜

既然系统中增加了一个轴,也就需要重新审视倾斜角的计算方法。简单的方法就是照旧计算 X轴,再以类似方式计算Y轴,不过记住要使用角度的余弦。(Y轴 使用角度的余弦)当重力为理想值 1g 时,输出加速度为:

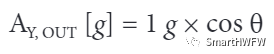
利用反余弦函数将加速度转换成角

其中,倾斜角θ单位为弧度。

我们很容易的发现如下关系：

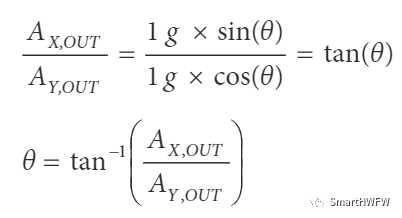
与单轴相比,使用两轴之比来确定倾角会使得增量灵敏度的确定变得十分困难。相反,假设所需的倾斜分辨率已知,则确定加速度计需达到的最低分辨率用处更大。假定一条轴的增量灵敏度随着另一条轴的增量灵敏度下降而上升,则净结果将是数值基本恒定的有效增量灵敏度。这 表示若针对某一角度,为达到所需的倾斜步长要求而选择加速度计,则该加速度计将具备足够的分辨率以应付所有角度。

三轴倾斜

单独确定加速度计每条轴与参考位置之间的夹角。参考位置通常选择器件的 x轴和 y轴位于水平面的方向上(0 g场),并且 z轴与水平面垂直(1g 场)。

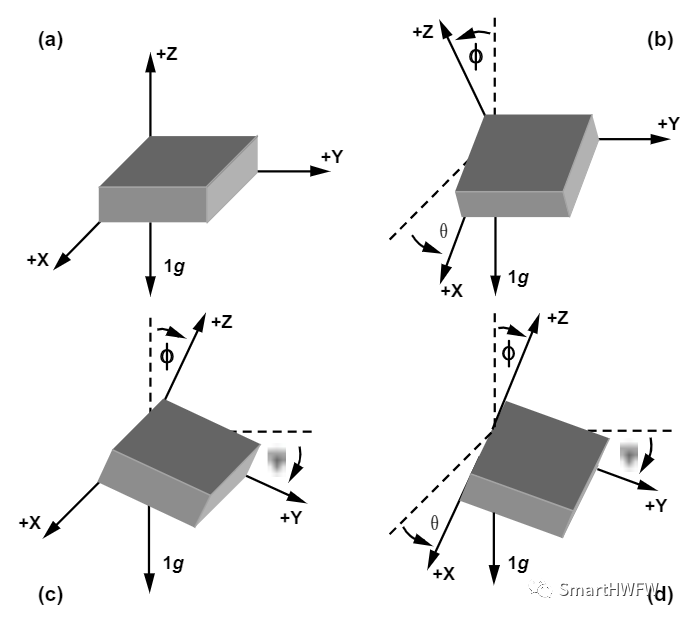
可利用基本三角恒等式计算倾角

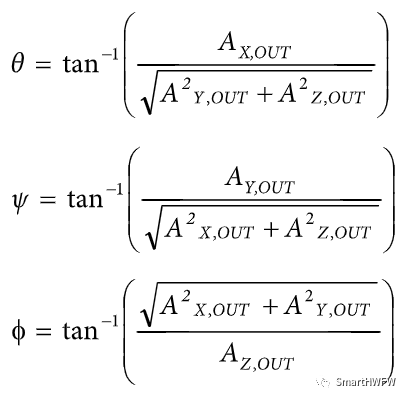
由于采用反正切函数和加速度之比,因此具有双轴示例中 提及的优势,也就是说有效增量灵敏度是恒定的,并且单 位范围内的角度可在所有点上精确测得。