为满足自动驾驶行车&泊车过程的纵向控制功能需求，需开发行车功能的纵向控制VLC以及泊车功能的轨迹速度规划TSP，其中，VLC负责将车辆纵向控制的加速度接口ax转化为驱动/制动力Fx（包括前馈控制与反馈控制），TSP进行S-V关系式拟合。

VLC控制算法简介

VLC技术方案简介

对于车辆的纵向控制，首先基于ACC模型并选择合适的控制算法，如极点配置、LQR、MPC等算法（可参考公众号相关文章），进而通过解算得到系统的控制输入量即期望加速度。忽略扰动项（前车加速度），得到ACC模型如下：

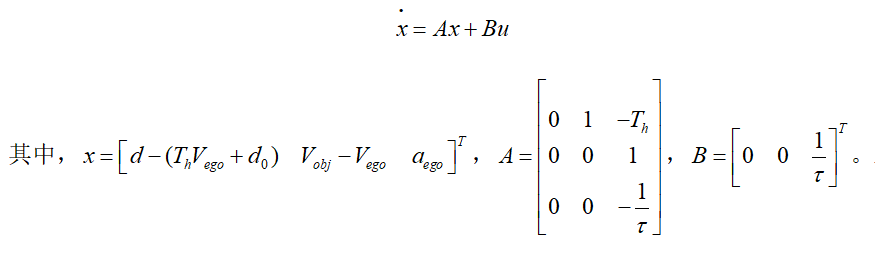
上述式子中：d为两车间的实际距离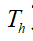，为车头时距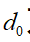，为两车间静止时的期望距离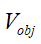，为前车速度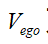，为本车速度，τ为一阶惯性环节的惯性时间常数。

控制算法在本处选用LQR，假设通过选取合适的Q及R后，解算得到反馈系数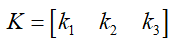：，进而得到期望加速度：

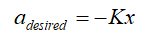
其中，K及x如上述算法所示。算法模型示意图如下图1所示：

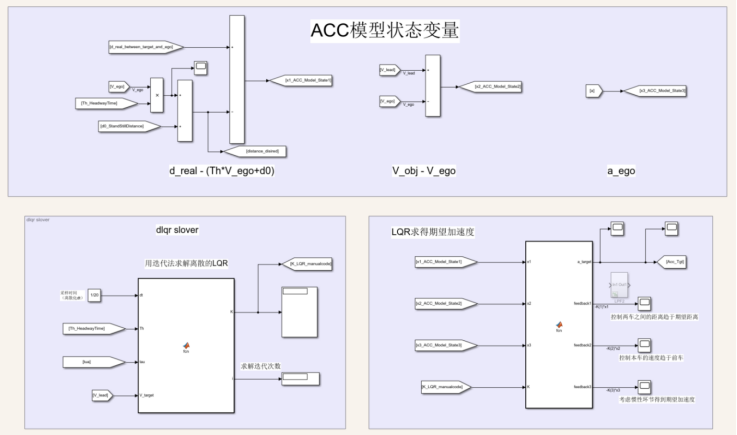
图1 ACC模型及LQR算法示意图

在得到期望加速度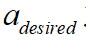之后，根据车辆的纵向行驶方程进一步计算得到期望的驱动扭矩或者制动压力。车辆的纵向行驶方程如下所示：

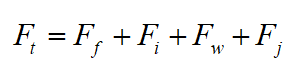
即：

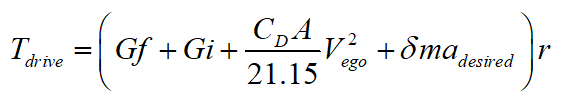
其中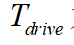，为期望的驱动力矩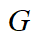，为本车的重力，i为道路坡度（纵坡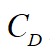），为空气阻力系数，A为迎风面积，δ为旋转质量换算系数，m为本车质量。

上述通过车辆纵向行驶方程所求得的期望驱动力矩为前馈值，由于模型存在建模的误差及不确定性，因此在此引入反馈对其进行补偿，本处所采用的反馈控制器为PID控制器，该控制器的输入为期望加速度与实际加速度的偏差，控制器的控制输出为驱动扭矩，该值则为反馈值。通过前馈与反馈的结合，使得该算法具备了更为优异的加速度跟踪性能。算法的示意图如下图2所示：

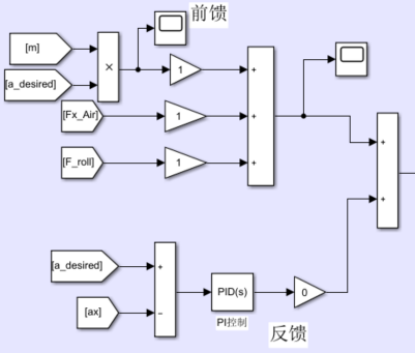
图2 前馈及反馈算法示意图

算法的仿真结果图（跟车场景：前车在过程中有启停）如下图所示：

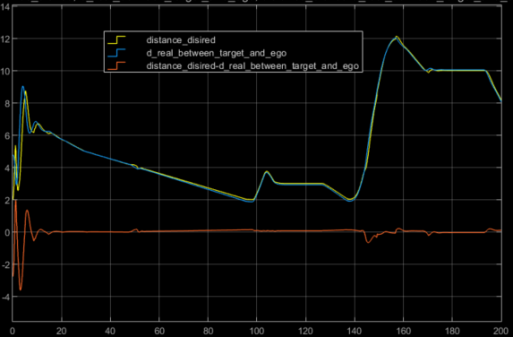
图3 两车间期望距离及实际距离对比结果图

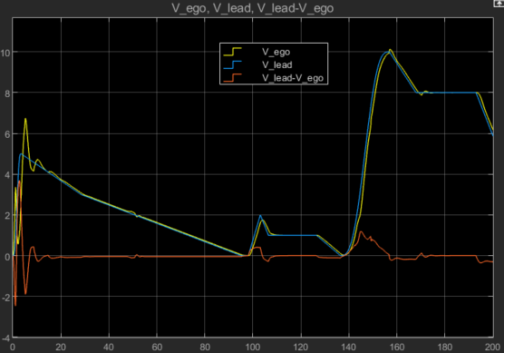
图4 本车速度及前车速度对比结果图

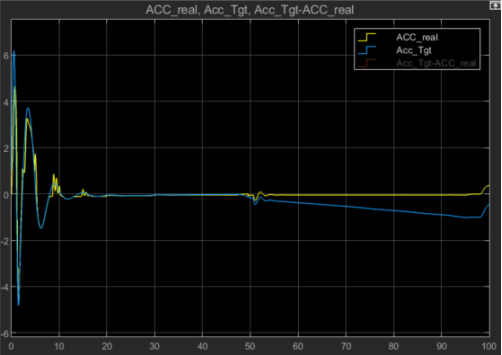
图5 ACC模型得到的期望加速度与本车实际加速度对比结果图

由图3、4及图5可以得到上述算法在跟驰前车上表现较好，对加速度的跟踪效果尚可。

上述参数中道路坡度、本车质量及状态变量中的本车速度需要通过参数估计及状态估计得到，而其他一些参数则可以通过传感器或者实验测量得到，在下面部分将详细介绍对于待估计参数及状态变量的参数估计算法及状态估计算法。

车速估计

在纵坡等路段，车辆的加速度传感器能够测得车辆的纵向加速度，但由于坡度的存在，其测量值往往可能存在较大偏差，需要通过滤波算法，对加速度进行重新估计，求得车辆速度、加速度的准确估计后，可根据加速度的测量值和估计值估计得到路面的坡度。

首先，利用轮速传感器测得的4个车轮转速估算车速：

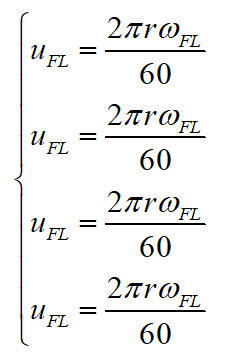
其中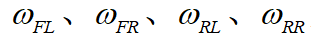，为4个轮的轮速，可由轮速传感器得到。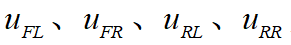为4个车轮旋转的当量车速。因为在车辆运动过程中，轮胎不可避免地存在驱动打滑、制动打滑等状态，所以需要对车轮打滑时地速度进行修正，此时使用上一时刻的速度与加速度估算当量车速。

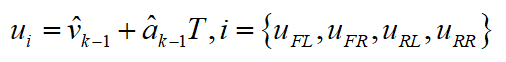
其中，T为采样周期，i为发生打滑的车轮。下一步将4个车轮旋转的当量车速按照从小到大进行升序排列：

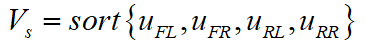
当汽车加速度为正值时，驱动轮可能发生打滑，从动轮的当量车速更加接近真实车速，选择第三大的当量车速作为参考车速；反之，选择第二大当量车速作为参考车速；否则将4个当量车速的平均值作为参考车速：

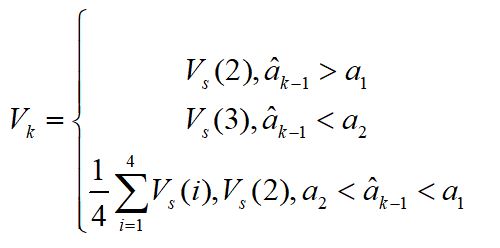
其中，是判断车辆驱动或者制动工况的加速度阈值，将由上式获得的参考车速作为车速的测量值。 在得到车速的测量值之后，再结合卡尔曼滤波对其进一步的处理，得到滤波后的车速值。具体过程如下： （1）建立系统状态方程：

假设车辆在一个周期内匀加速行驶（CA模型），状态变量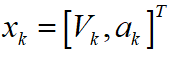，其中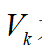为当前车辆行驶的速度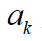，为当前车辆行驶的加速度。可得到系统的状态方程：

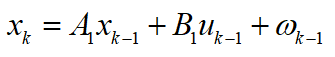
其中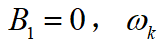，为高斯白噪声。当采样周期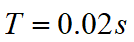时，状态转移矩阵为：

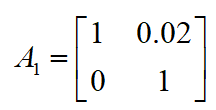
（2）建立测量方程：

车辆在当前周期内的行驶速度将使用上述的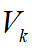，加速度则通过加速度传感器（IMU）获得，则测量方程为：

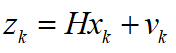
其中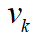，为测量噪声。由于系统状态完全可测，故观测矩阵为H为单位矩阵。 （3）卡尔曼滤波： 给定滤波过程的初始状态，再根据如下所示的卡尔曼滤波的5个公式即可对车速进行滤波，最终得到车速的估计值及加速度的估计值。

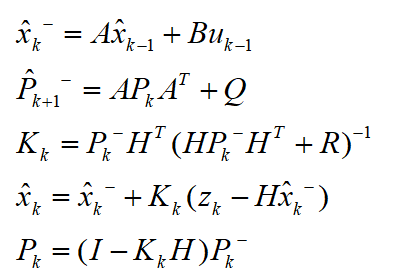
其中，测量信息为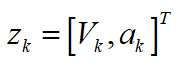：。 坡度估计 设上述通过卡尔曼滤波估计得到的加速度为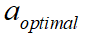，则可以根据下式估算道路坡度i：

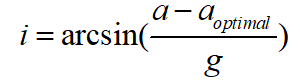
其中，a为IMU测得的车辆纵向加速度，g为重力加速度，该方法的原理示意图如下所示：

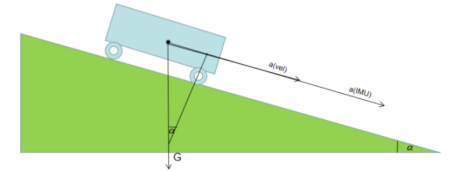
图6 纵向加速度测量

质量估计 对车辆纵向行驶方程进行变形得：

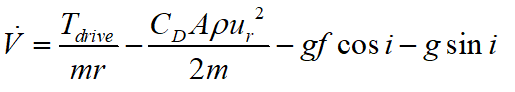
考虑到公路的设计规范，道路坡度一般较小，因此对上式进行简化，得：

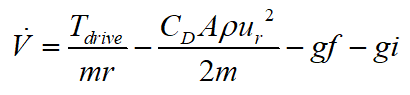
假设质量变化及坡度变化为一个慢时变过程，可得：

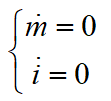
选取V、m、i为状态变量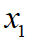，构建状态空间表达：

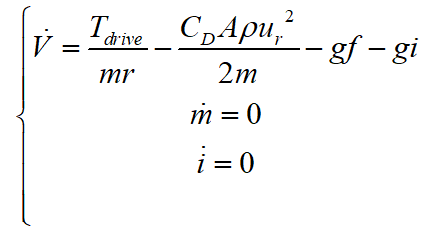
对其进行离散化得：

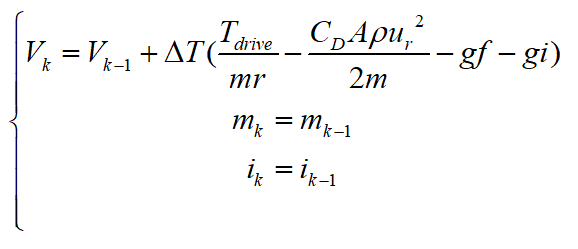
选取车速作为观测量，则系统的测量方程为：

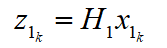
由上述可得系统的状态空间表达：

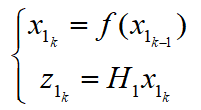
对上述系统使用扩展卡尔曼滤波即可重构得到系统状态，即获得了质量的估计值。

TSP技术方案

 TSP纵向速度规划方案

在自动泊车场景下，本车周围通常存在许多的障碍物，如：墙壁、立柱、旁边车位停放的车辆等。如何在不发生碰撞的情况下，将车辆自动泊入所选定的车位，是自动泊车中的主要技术点，即路径规划。而在完成了路径规划之后，也需要对其进行相应的速度规划，使得车辆能够安全、高效、舒适的完成自动泊车任务。

从人类驾驶员的经验出发，一般距离障碍物越近时，人类驾驶员往往会选择降低车速，缓行通过，因此，本次TSP纵向速度规划主要是基于上述经验，对泊车过程中的本车速度进行规划。

由上所述，本次TSP纵向速度规划目标是得到本车速度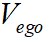与本车与障碍物之间的距离d的关系。在经过分析后，本次规划选取三次多项式曲线来进行速度规划，即速度与加速度的多项式映射关系为：

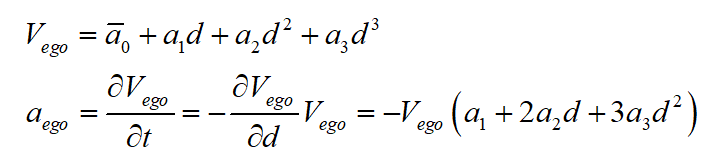
首先确定边界条件。在规划的初始点，本车与障碍物之间的初始距离为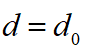，而本车当前速度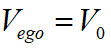，当前加速度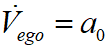；在规划的结束点，车辆成功泊入车位，本车与障碍物的最终距离为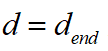，本车规划的速度为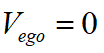。将上述两个边界条件带入三次多项式中，可得：

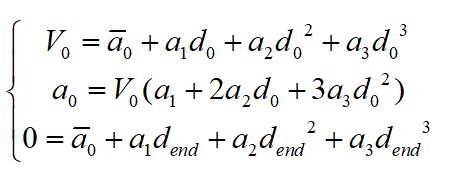
考虑到上述三个边界条件带入三次多项式曲线后得到的方程组求解的复杂度，在此处通过引入中间变量的方式对其进行变形，以简化求解，提高算法的实时性。通过分析，选取本车从泊车开始累计的行驶距离S作为中间变量，该中间变量与d之间的关系如下式：

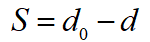
将上式带入三次多项式曲线中，可得到以S作为自变量的新的三次多项式曲线，表达式如下：

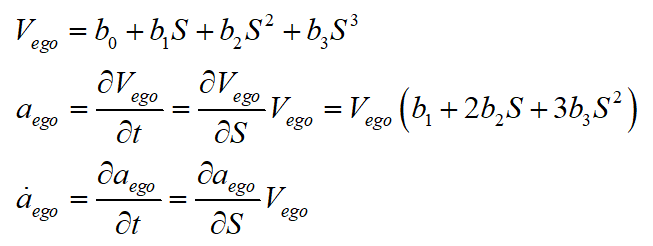
此时，再将三个边界条件带入新的三次多项式曲线中可得：

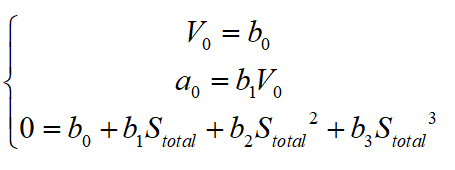
其中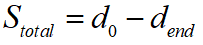，为泊车过程中本车所行驶过的总距离。对上式进行解方程组可得：

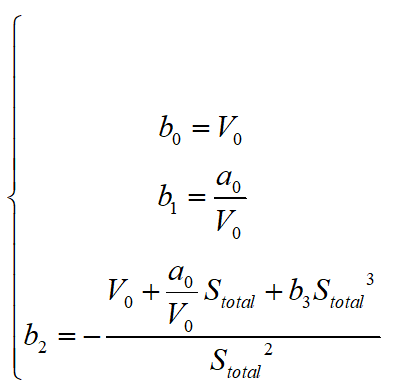
将上式方程组的解代回到速度曲线的三次多项式，可得：

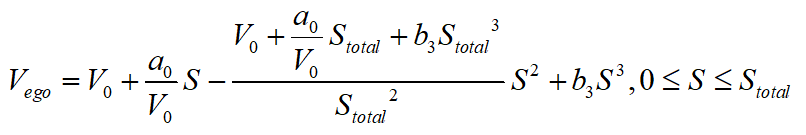
因此，由三个边界条件所得到的三个约束条件，使得三次多项式曲线的自由变量（系数）只剩下一个，最后将结合优化的方法来求得该系数的最优值，在此处该自由变量为。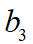

对上式两边同时对时间求一阶及二阶导数，可得速度和加速度分别为：

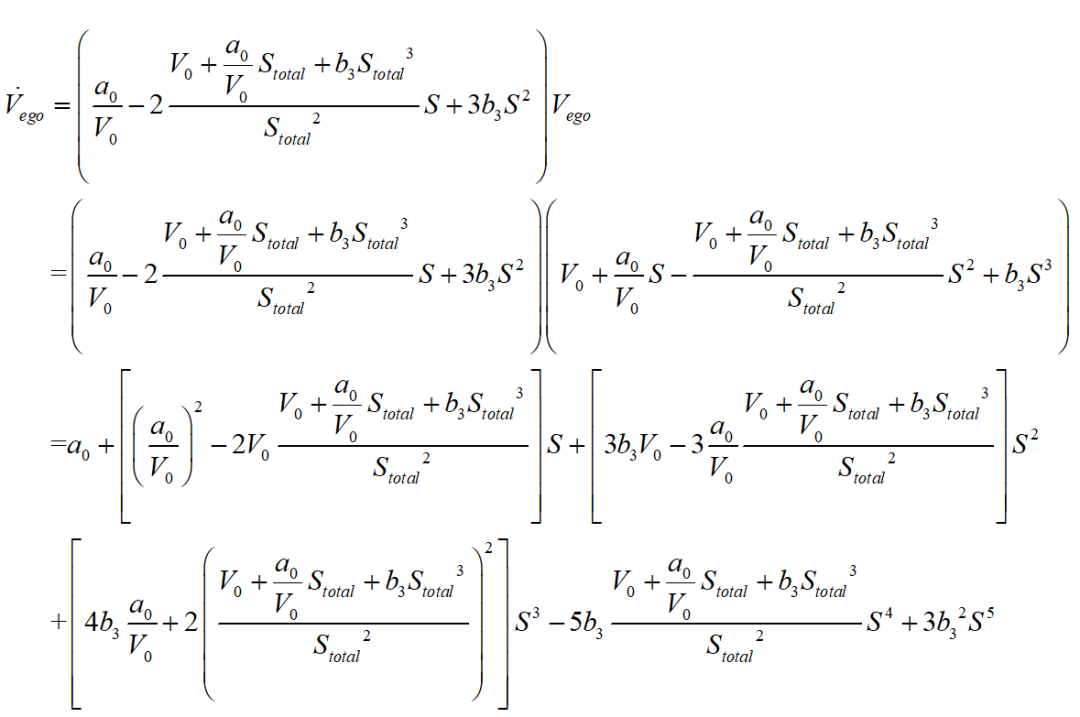
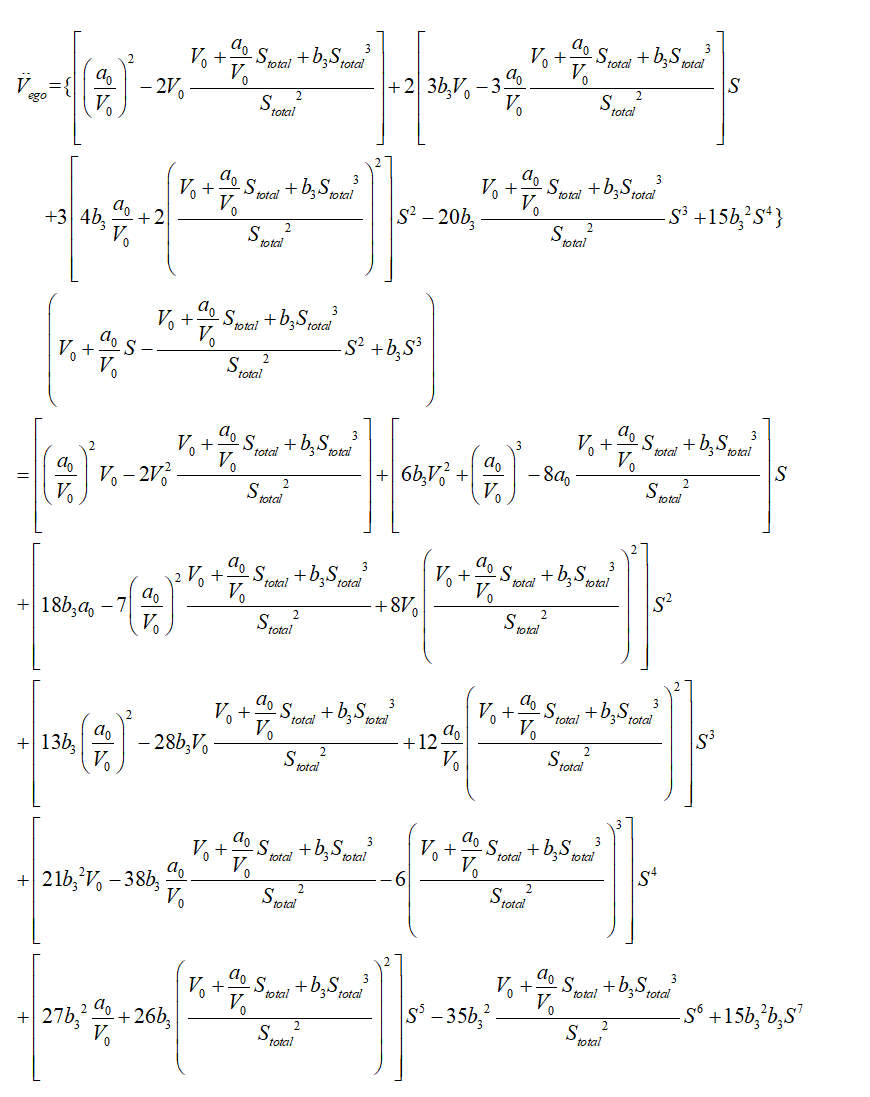
纵向速度优化模型

从舒适性的角度出发，加速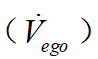度与冲击度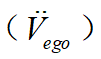应当尽量的小；从效率的角度出发，希望车辆完成泊车任务的时间尽可能的短；因此，在考虑上述目标后，设定目标函数如下：

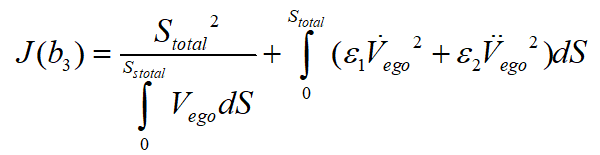
其中，目标函数中的第一项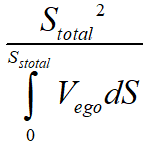的物理意义为完成泊车过程所用的时间，即对应效率的目标，第二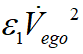项及第三项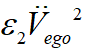则对应舒适性的目标即平稳泊车的目标。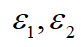为优化的权重系数。最后将上面的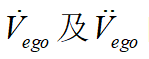的表达式带入该代价函数，化简可得关于变量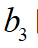的代价函数如下式：

上述代价函数为关于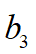的一元多次函数，目标是找到最优的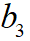让代价函数取得最小值。对于一元函数求极值的问题，使用KKT原理是比较有效的方法，因此，对上式关于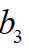进行求导，并令该式等于0得到若干个解，最后比较这几个点的函数值即可确定最优的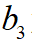解，而根据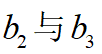的关系也得到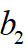，至此所规划的速度曲线已经被唯一确定，完成了TSP纵向速度规划。

泊车速度规划求解

TSP车速规划相关的算法如下图示：

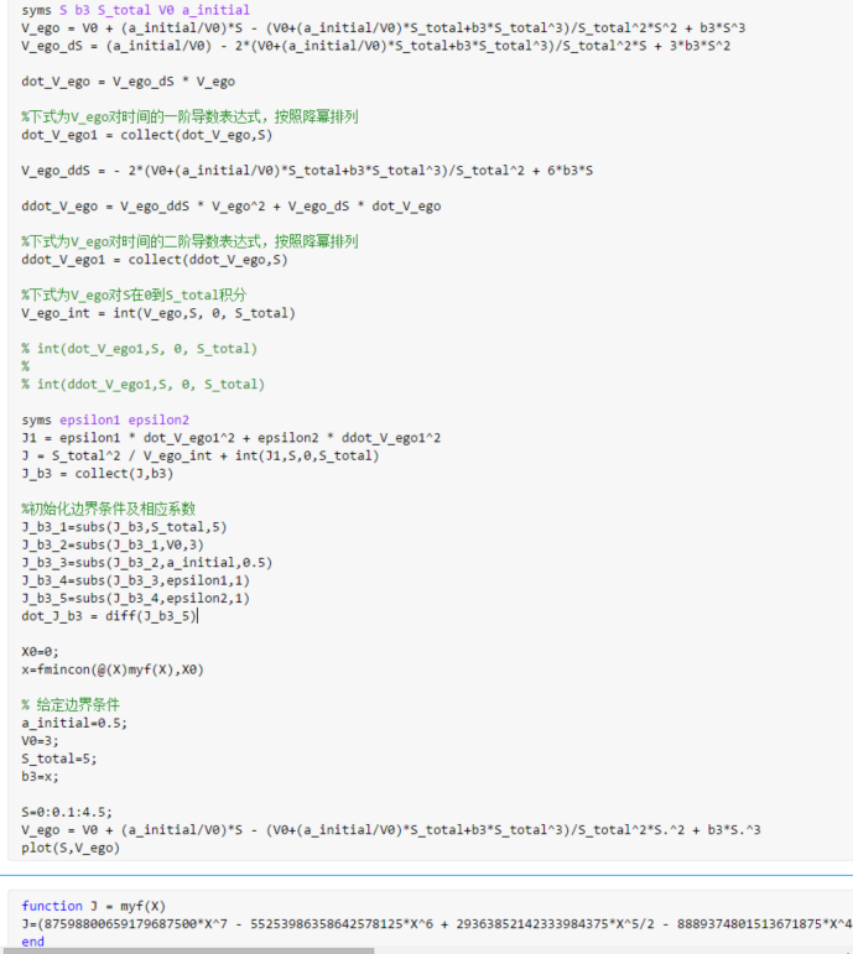
在本次的算法测试中初始条件设置为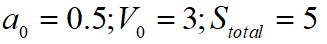：，最后求得的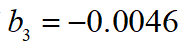，完成整个泊车过程的时间为2.286s，带入得到：

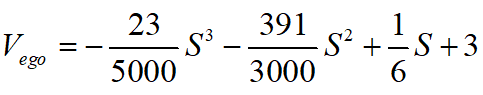
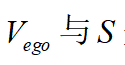，的关系图如下图所示：

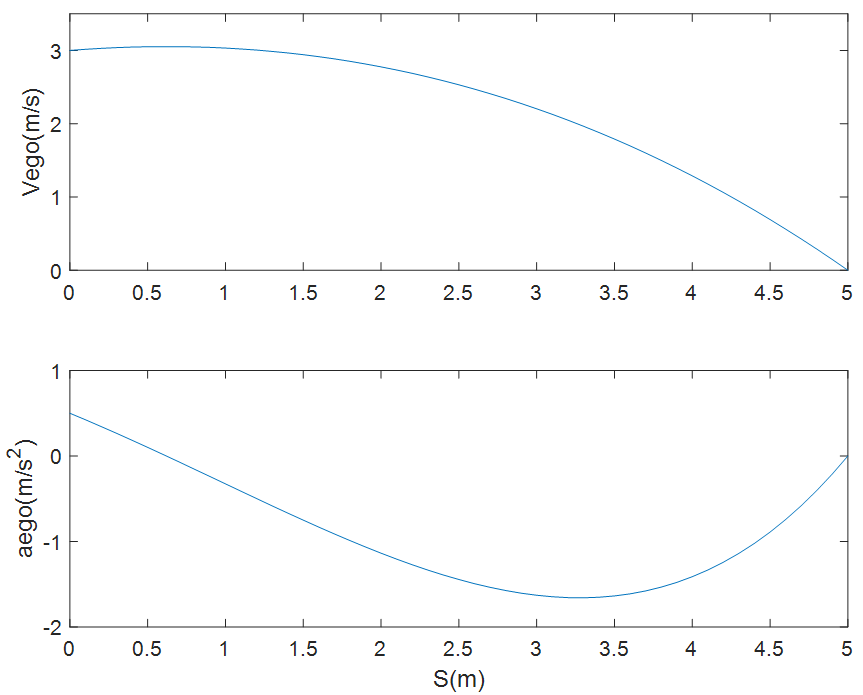
图7 规划的速度与加速度

上述算法还是较复杂，考虑到其实时求解问题，可将其简化，假设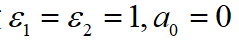，则简化后关于变量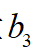的代价函数如下式：

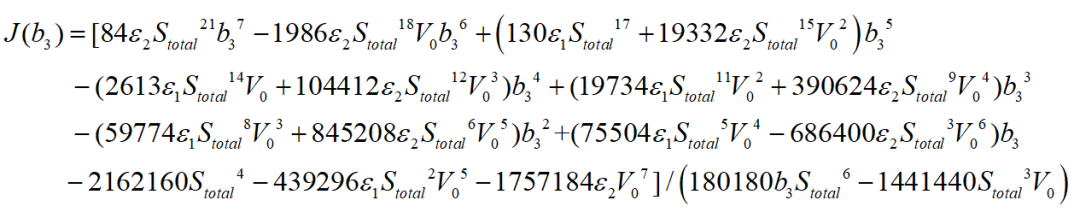
其极值点为：

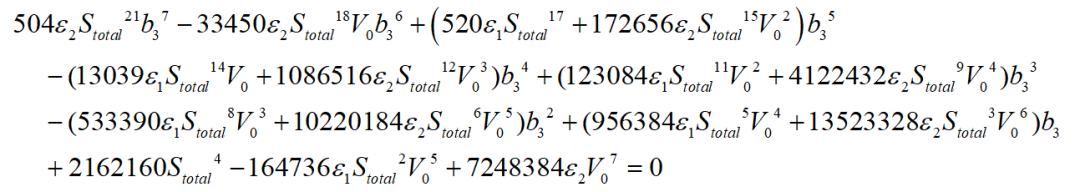
考虑到上述极值点条件有多个可行解，快速寻找其最优解也是一个较为复杂的问题，可利用泊车完成一半时候的规划速度非负这个条件来加以判断，因此设定验证条件如下所示：

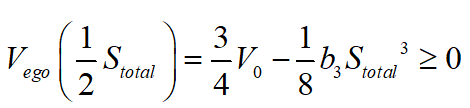
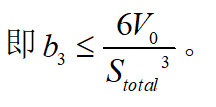
在同样边界条件下可求得有两个可行解，分别如下图所示。

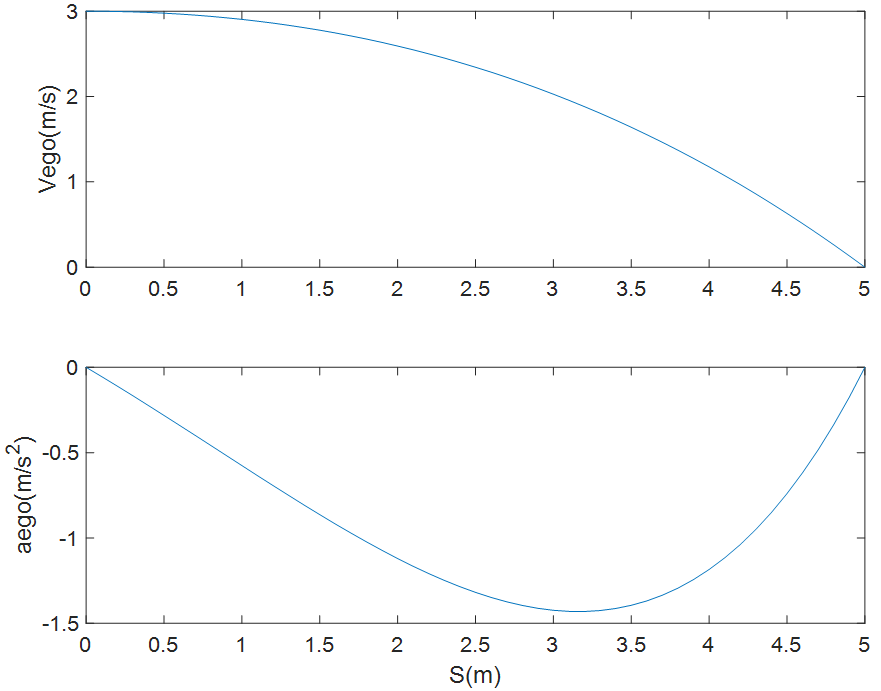
图8 规划的速度与加速度（可行解1）

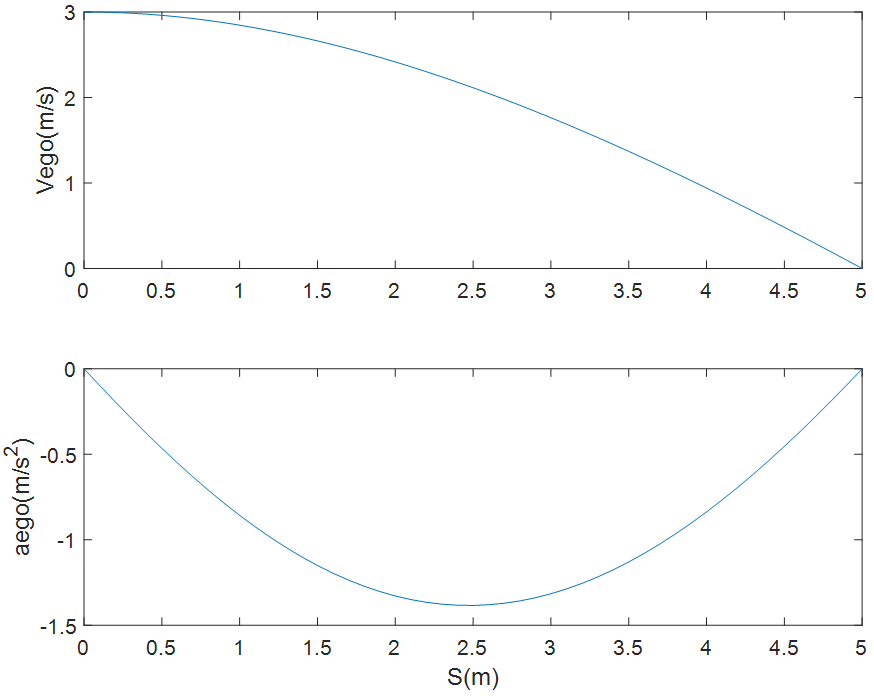
图9 规划的速度与加速度（可行解2）