技术咨询
代买器件
商务客服
研发客服什么是梯形加减速
如下图所示，假设该装置使用步进电机实现物体X的移动，系统要求物体X从A点出发，到B点停止，移动的时间越短越好且系统稳定。
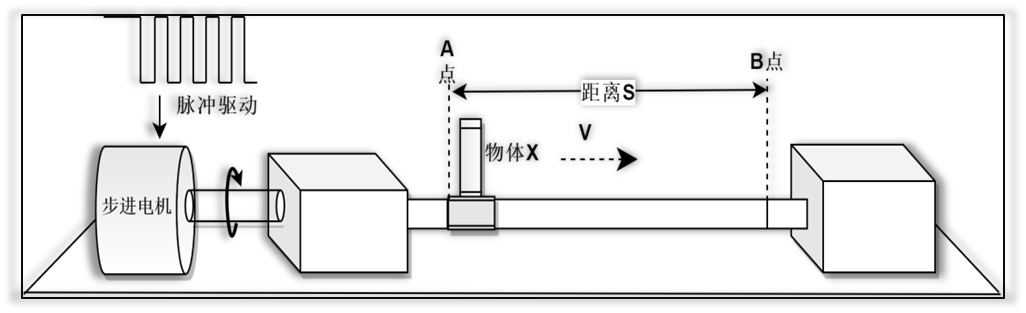
使用梯形加减速
OA段为滑块的加速部分、AB则是匀速部分，BC则是减速部分。因其图像呈现梯形，所以我们把这种运动变化称之为梯形加减速
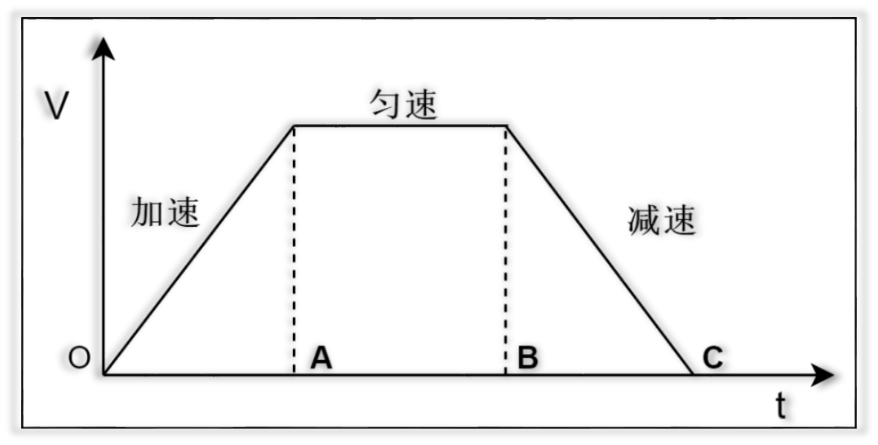
使用加减速的理由
为什么要使用加减速呢？步进电机有一个很重要的技术参数：空载启动频率，也就是在没有负载的情况下能够正常启动的最大脉冲频率，如果脉冲频率大于该值，步进电机则不能够正常启动，发生丢步或者堵转的情况；或者也可以理解为由于步进脉冲变化过快，转子由于惯性的作用跟不上电信号的变化。所以要使用加减速来解决启动频率低的问题，在启动时使用较低的脉冲频率，然后逐渐的加快频率。
梯形加减速算法特点
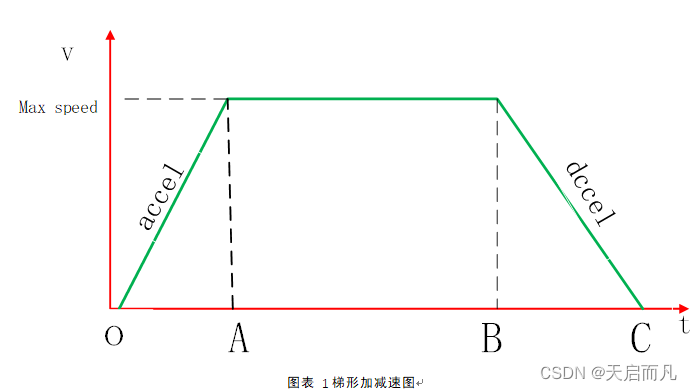
梯形加减速一共分为三个阶段，OA 加速部分、AB 匀速部分 和 BC 减速部分。在 OA 加速过程中，由低于步进电机的启动频率开始启动（模型中由 0 启动），以固定的加速度增加速度到目标值；在 AB 匀速过程中，以最大速度匀速运动；在 BC 减速部分中，以加速度不变的速度递减到 0；这种算法是一种在加速过程和减速过程中加速度不变的匀变速控制算法，由于速度变化的曲线有折点，所以在启动、停止、匀速段中很容易产生冲击和振动。
算法基础
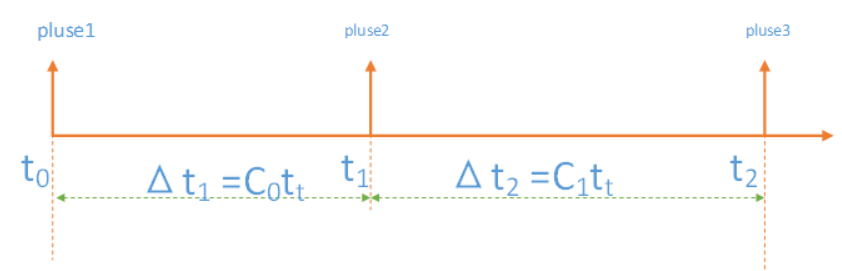
梯形算法要求的变量
6、在一个电机匀加速到一定速度，再匀减速的情况下，如下图：
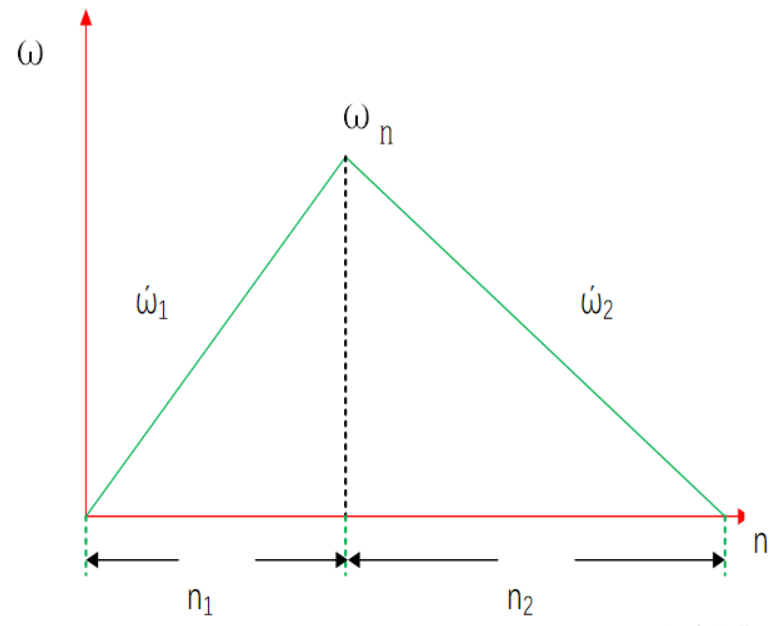
从0加速再减速到0的速度示意图
7、求加减速步数
对于步进电机加减速阶段来说，由于已经设定好了步进电机加速度、减速度、最大速度和总运行步数，所以说一共分为2种情况：
（1）电机能够加速到给定的最大速度，匀速运行一段时间后，再减速到0
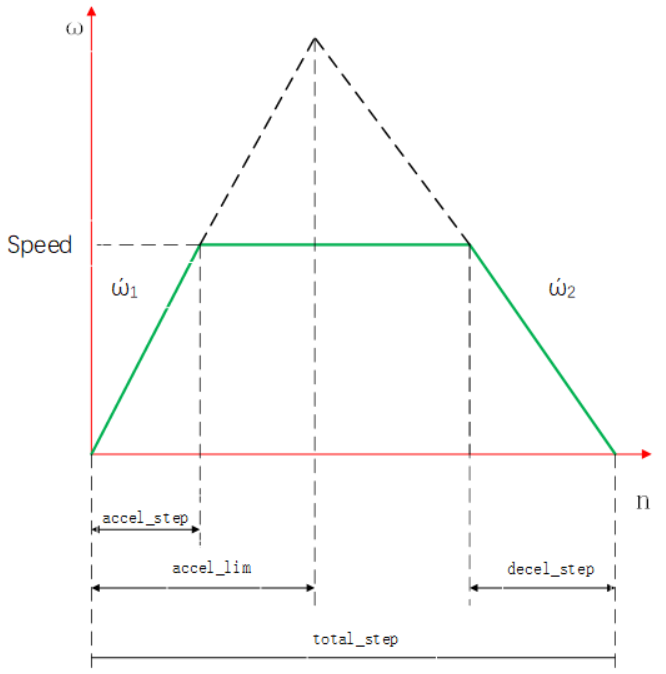
电机加速到给定speed再减速的示意图 
（2）由于运动距离过短，电机无法加速到最大速度即开始减速：
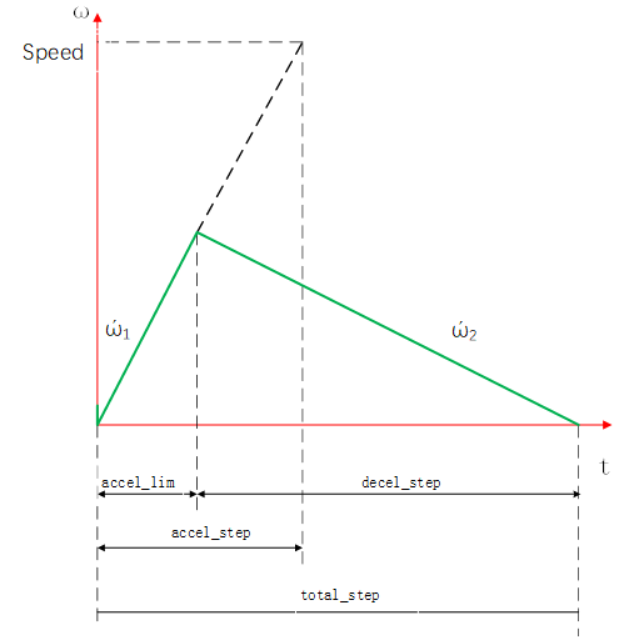
电机无法加速到给定speed就减速的示意图
通过以上推导，我们求出了梯形算法要求的所有变量。
算法优化 由于算法在计算过程中涉及到一些浮点型运算，大量的浮点型运算会使得效率大大降低，为了使得计算速度得到更好的优化，我们做如下优化：
相关文章
