引言

数控系统在工矿领域已得到广泛应用，计算机数控系统通过对数字化信息的处理和运算，并转化成脉冲信号，实现对电机的控制，进而控制数控机床动作和零件加工。随着嵌入式技术的发展，我们可以设计规模更小，成本更低，功能更特定的嵌入式系统来完成传统计算机数控系统所完成的工作。

1、设计方案

本系统以嵌入式处理器STM32和FPGA芯片为核心，运动控制方案中的处理部分都放在FPGA内部实现。这是1种硬件软化的方案，即具有软件可编程、可重构的特点，又有硬件那样高性能、高可靠、高一致性的优点。其系统原理框图如图1所示。

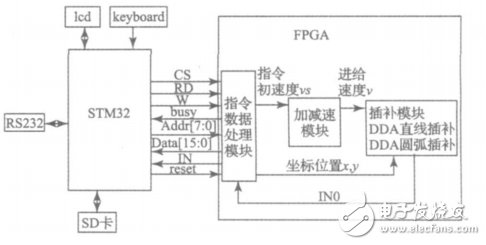
图1  系统原理

STM32从SD卡中读取数据文件并进行相关算法处理，通过键盘扫描电路设置系统加减速的初始速度、最大速度、加速度的初始值以及一些控制参数。将相应参数传送到FPGA进行处理，最后由FPGA控制输出脉冲和脉冲间延时，通过高光耦隔离后输出，控制电机的运转。通过RS232实现和上位机数据通信以及驱动LCD完成人机交互工作。FPGA主要用来实现指令和数据处理模块、加减速模块、插补功能模块（包括直线插补和圆弧插补）等运动控制算法。

2、运动控制算法在FPGA中的实现

2.1、速度控制算法在FPGA中的实现

为避免电机在启动、运行以及换速过程中使各轴产生超程、冲击、失步和振荡的现象，保证运动机构的平稳和准确定位，这就要求电机在各程序段转接时具有一个加减速的过程，使其平滑的过渡。大多运动控制系统都拥有梯形加减速和S型加减速功能。由于梯形加减速算法简单，系统响应快，效率高等优点，结合本课题要解决的主要问题以及应用的相关领域，课题在传统梯形加减速的基础进行改进来实现脉冲的输出。梯形加减速算法采用脉冲叠加的方法在FPGA内部的实现，即：以某一时钟为基准，将其进行n次分频后产生互不重叠的不同频率的n种脉冲，然后提取所需要的几种脉冲以式（1）进行叠加，从而输出连续可调的、不同频率的脉冲来完成加减速运算。式（1）如下所示：

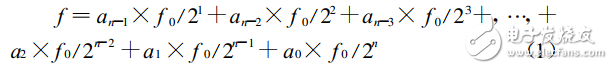
由式（1）可知f0/2n为对基准脉冲的分频，分频过程中通过对分频计数器的位数进行设置来产生不同频率且不重叠的脉冲。系数a［N:0］是单位时间产生的脉冲数，即脉冲速率。由此可以得出该方法下的系统逻辑结构电路图如图2所示。

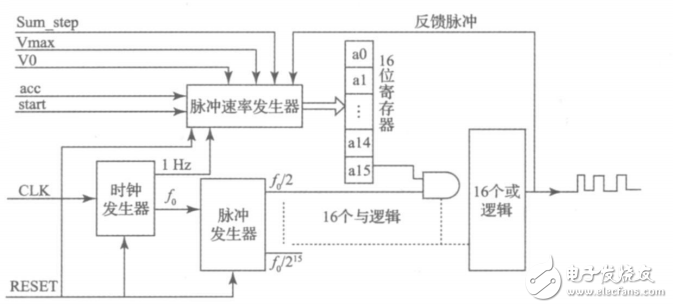
图2  系统逻辑结构电路

在图2中，系统主要包括时钟发生器、脉冲速率发生器、脉冲发生器和叠加器（包括n位寄存器、n个与逻辑和n个或逻辑）4个单元。时钟发生器主要对系统时钟进行分频产生基准脉冲;脉冲速率发生单元主要产生每单位时间输出的脉冲数，即脉冲输出速率单元，以及在里面完成加减速的判断等功能;叠加单元主要将来自脉冲速率发生器的每单位时间脉冲数存储在n位的寄存器中，然后完成和n种互不重叠的脉冲叠加的过程。

图3为本设计在QuartusII中的仿真波形，值得说明的是为加快仿真速度，仿真前对某些参数进行过修改。

图3  仿真波形

2.2、DDA直线插补在FPGA中的实现

如果所选取的脉冲当量足够小，函数的积分运算就变成了变量的求和运算，则用求和运算来代替积分运算所引起的误差可以不超过容许的数值。这样，可以采取2个寄存器（被积函数寄存器Jv和余数寄存器Jr）和1个全加器Q构成数字积分器。比值积分法取累加次数等于终点坐标值中最大的1个，如进行累加运算，则该坐标累加和每次皆为1，每次皆发一个进给脉冲，作为进给脉冲。从而使每次的进给速度达到最大且均匀，所以加工的效率、加工的质量都大为提高。比值积分法直线插补逻辑框图如图4所示。

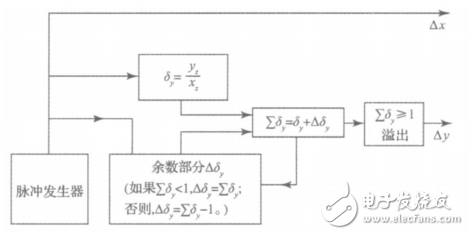
图4 比值积分法直线插补逻辑

DDA直线插补在QuartusII中的仿真波形图如图5所示。插补起点为（0，0），终点为（20，9）的直线。

图5中x，y为输入，D为累加寄存器，D1为溢出脉冲，D2为余数寄存器。xpp，ypp为输出脉冲。将插补的结果与实际图形比较如图6所示。

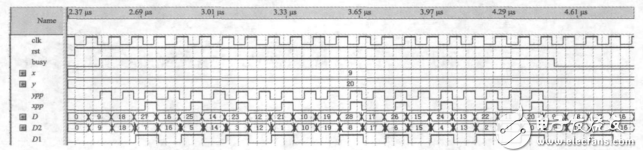
图5  仿真波形

放起点坐标Yq和Xq。插补过程中，每当Y轴溢出一个脉冲，JVx应修正为JVx+1;而每当X轴溢出一个脉冲，JVy应修正为JVy-1。当圆弧由起点S（Xq，Yq）移动到终点E（Xe，Ye）时，X积分器JVx中的Y值将由Yq变为Ye，Y积分器JVy中的X值将有Xq变为Xe。对于修正过程中，加减1的取值要根据不同的曲线所在的象限和走向来决定。

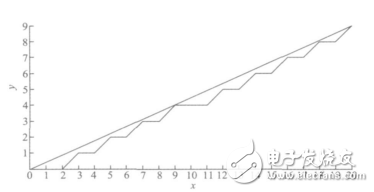
图6  插补结果与实际直线的比较

2.3、DDA圆弧插补在FPGA中的实现

DDA圆弧插补也是由被积函数和余数累加器够成的［6，9？？12］。对于被积函数寄存器和余数寄存器的位数确定现在以第I象限逆圆为例来分析圆弧插补的被积函数和余数。对于圆弧插补，其被积函数是变量，是变动的值，换句话说它的被积函数寄存器中的值要不断进行修正，并且圆弧插补时JVx对应Y轴坐标，JVy对应X轴坐标。例如，对图7所示的插补来讲，在插补开始时，JVx和JVy中分别存放起点坐标Yq和Xq。插补过程中，每当Y轴溢出一个脉冲，JVx应修正为JVx+1;而每当X轴溢出一个脉冲，JVy应修正为JVy-1。当圆弧由起点S（Xq，Yq）移动到终点E（Xe，Ye）时，X积分器JVx中的Y值将由Yq变为Ye，Y积分器JVy中的X值将有Xq变为Xe。对于修正过程中，加减1的取值要根据不同的曲线所在的象限和走向来决定。

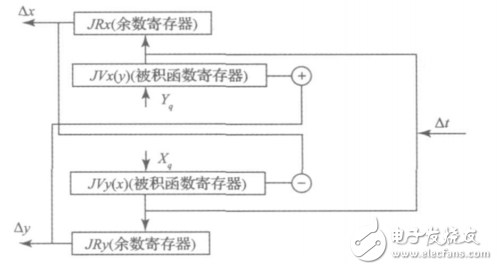
图7 积分法圆弧插补逻辑

DDA圆弧插补在QuartusII中的仿真波形，插补起点为（11，0），终点为（0，11）的圆弧。如图8所示。

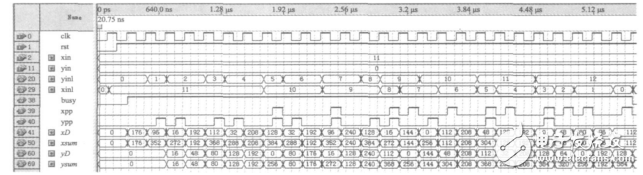
图 8  仿 真波形

图8中x，y为输入，xsum，ysum为累加寄存器，xD，yD为余数寄存器。xpp，ypp为输出脉冲。将插补的结果与实际图形比较如图9所示。

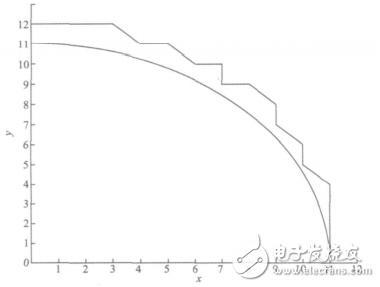
图9  插补结果与实际圆弧的比较

3、结论

为验证所设计芯片的插补功能，编写了STM32粗插补程序，将产生的粗插补坐标增量发给FPGA进行插补实验，得到了理想的插补输出脉冲，控制步进电机的运转从而雕刻我们所需要的补轨迹图形。又编写了STM32脉冲处理程序，读回了FPGA的输出脉冲，并由串口发送给PC。最后通过编写PC的串口通信程序以及根据插补脉冲绘图的程序，把FPGA的输出脉冲绘制成了插补轨迹图形。最终绘图结果显示，在20M输入时钟频率下，由插补脉冲生成的插补轨迹图形正确，验证了本文设计的插补算法功能的正确性。插补芯片达到了高速插补功能要求。