0   引言

（Butterworth Filter）也被称作最大平坦滤波器。其特点是在通频带内，其频率响应曲线最大限度平坦、单调递减无波纹产生；而在阻频带内，其频率响应曲线逐渐下降为零。这些优点使其在信号处理领域有着广泛的应用。对于滤波器的性能一般考虑其幅频特性，但对于更深层次的信号处理应用方面，滤波器的相频特性也是其重要特性之一。尤其是在多点激励、载荷建立以及传递路径识别等方面问题的研究中具有重要作用。

1   分析

连续时间巴特沃斯低通滤波器可用式（1）表示。

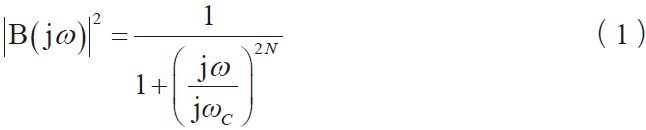
式中：B(jω) 为连续时间巴特沃斯，ω 为频率，ω_C 为滤波器截止频率，N 为阶数，该滤波器Bode 图如图1 所示。

将式（1）转换为Laplace 域分析，即令s = jω，可得到式（2）。

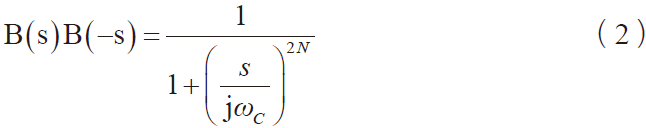
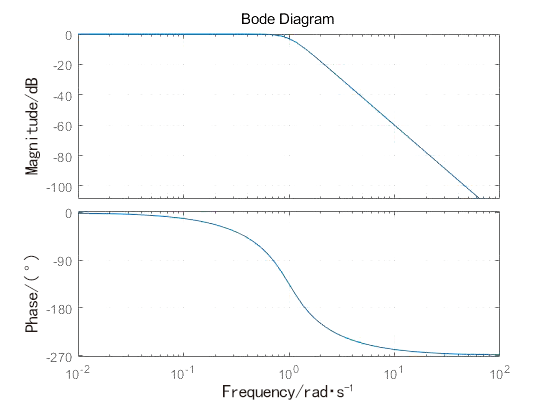
图1 Bode图

求解式（2）的极点，可得式（3）。

对极点作归一化处理，即令：

作归一化巴特沃斯滤波器的拉普拉斯域平面，可以得到2N 个以虚轴Im 对称的极点，以N = 3 为例其极点分布如图2 所示，所有极点都均分在以原点为中心的单位圆上。

为形成因果稳定系统，取左半平面极点构建式（5）的。

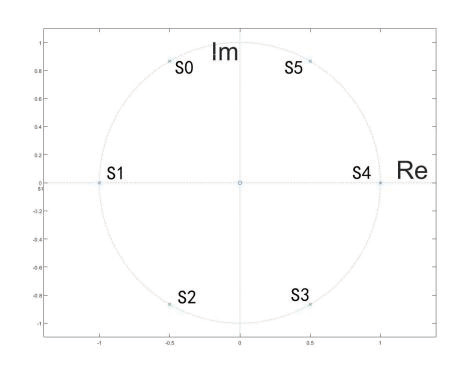
图2 极点分布图

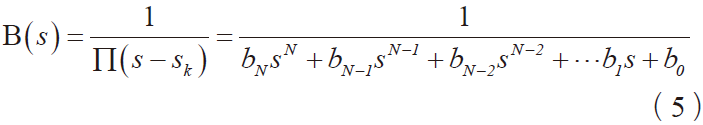
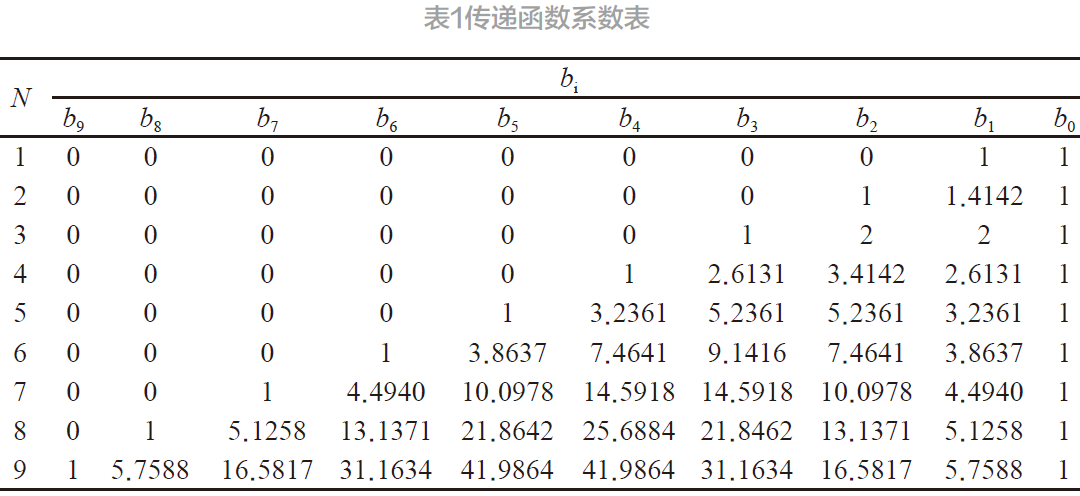
其中多项式系数b_i可构为建归一化N 阶巴特沃斯滤波器的传递函数系数，不同阶数系数如表1 所示。

对应不同阶数N， 绘制归一化巴特沃斯滤波器Bode图如图3 所示。

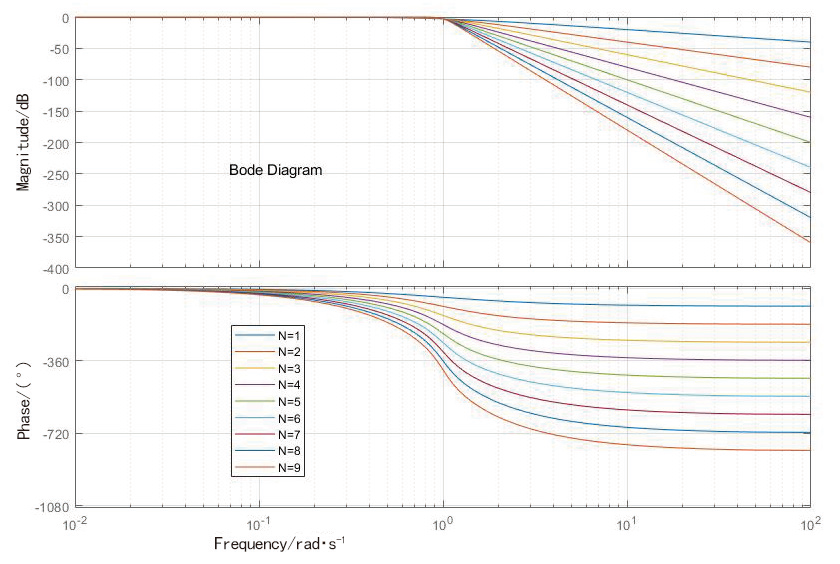
图3 归一化巴特沃斯滤波器Bode图

2   数字滤波器设计实例

现以表2 所述滤波器性能参数，实例设计巴特沃斯型数字滤波器。

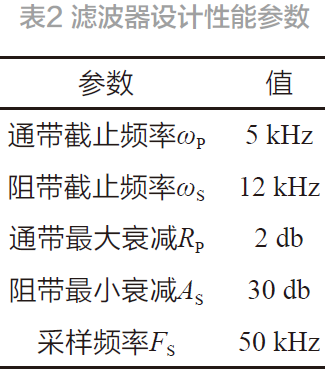
针对通带截止频率与阻带截止频率设计要求，建立式（6）与（7）的滤波器设计约束条件。

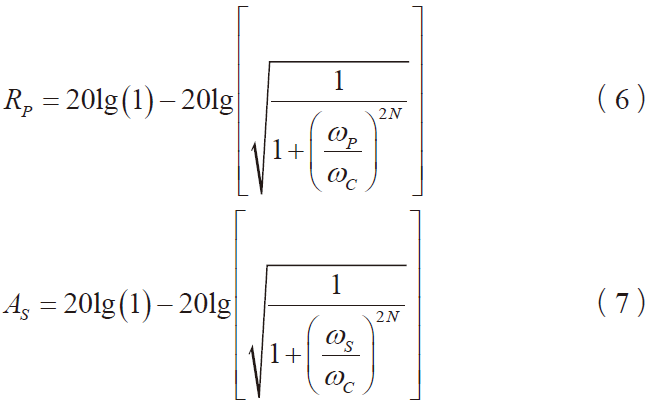
通过约束条件，可通过式（8）得到理论设计阶数。

由于阶数需为整数，将理论阶数N* 向高阶取整以得到N，并代入式（9），即可得到截止频率ω_c。

经计算，N = 4，ω_c = 5.275 kHz，通过归一化滤波器系数，即可表得到滤波器的传递函数为式（10）。

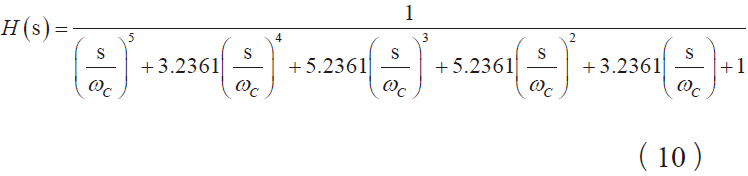
采用法，即通过式（11）完成s 域到z域的映射。由此即可得到在采样频率下的数字滤波器传递函数。

3   滤波器的仿真分析

仿真过程中，通过构建两路不同频率正弦波信号x1和x2进行叠加作为输入，其中x1为300Hz，x2为15kHz。按图4 所示原理图，将叠加信号通过采样器采样后输入数字滤波器，通过示波器分别显示原始叠加信号、低频信号与滤波信号的波形。

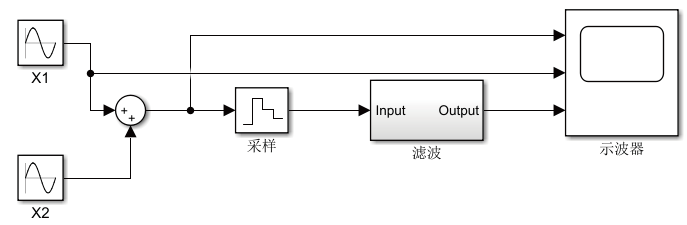
图4 仿真系统原理

通过图5的波形分析可以看出，该滤波器可以很好的将高频信号滤除，滤波信号的波形基本能够还原输入的低频信号。只是在幅值上有0.028%的衰减，相位上存在127.433μs的延迟。

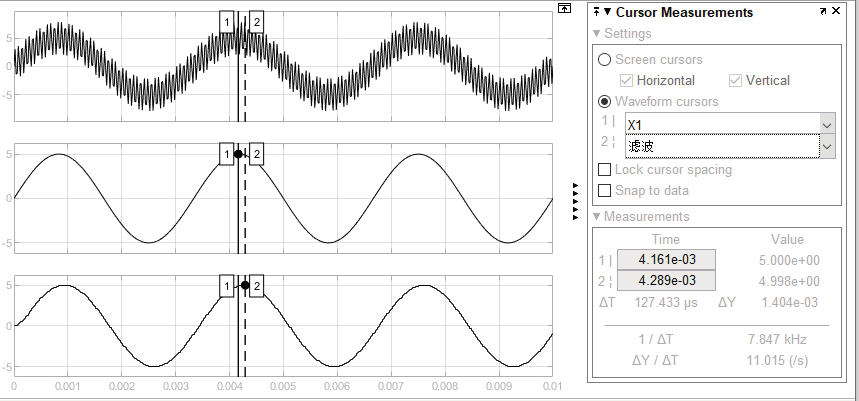
图5 波形分析

4   结束语

本文从巴特沃斯滤波器的设计原理着手，通过极点分析推导了巴特沃斯系数表的构建方法，并分析了设计阶数对滤波器的幅频特性与相频特性所产生的影响。通过结合实例指标参数要求，使用法完成了巴特沃斯型数字滤波器的设计。最后通过仿真分析，验证了该数字滤波器的滤波效果，结果表明在通频段信号的幅值有微弱的降低，相位有少量滞后，但总体还原程度较高，效果理想。

参考文献：

[1] [美]ALAN V O,等.信号与系统[M].3版.刘树棠,译.北京:电子工业出版社,2013.

[2] 龚作豪,沈君凤.巴特沃斯低通滤波器的仿真设计[J].信息通信,2014(139):40-41.

[3] 仲帅.基于改进粒子群算法的数字滤波器设计及应用[D].长春:吉林大学,2016.

（本文来源于《电子产品世界》杂志2022年12月期）