或统计中的第四中心矩,通常用于估计信号(或数据)的统计分布的形状。它被广泛用于检测非正态性 在数字通信系统、无源微波辐射测量、时间序列分析、图像处理和射电天文学中使用的通信接收器接收的信号中,仅举几例。它还可用于检测某些调制方案中的能量和功率,以及测量通信系统的系统间干扰。在大多数情况下,峰度主要用于检测是否存在强烈的人为射频干扰,这些干扰会污染分布并使其不正常。
本文引用地址:或统计中的第四中心矩,通常用于估计信号(或数据)的统计分布的形状。它被广泛用于检测非正态性 在数字通信系统、无源微波辐射测量、时间序列分析、图像处理和射电天文学中使用的通信接收器接收的信号中,仅举几例。它还可用于检测某些调制方案中的能量和功率,以及测量通信系统的系统间干扰。在大多数情况下,峰度主要用于检测是否存在强烈的人为射频干扰,这些干扰会污染分布并使其不正常。峰态计算如公式 1 所示。
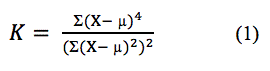
在哪里:
K 是峰度值
X 是输入数据
是计算中考虑的 N 个样本的平均值
代表平均值
在正态(高斯)分布的情况下,峰度为 3。由于我们正在计算有限数量样本的峰度,因此估计值会有一些由估计误差定义的不确定性,因此对于正态分布,该值将是 3 ± d(估计误差)。因此,对于被视为正态分布的给定输入数据集,Kurtosis 的值必须位于这些限制范围内。
在 FPGA 或其他 DSP 平台上计算峰度是计算密集型的,主要是因为它需要除法运算。本设计思想完全避免了除法,使用两个乘法器和其他模块来判断输入数据是否通过峰态测试。这种方法利用了这样一个事实,即为了检查分布的正态性,只需要确定峰度值是否在定义的范围内。
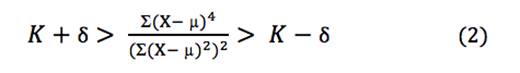
计算峰态的传统方法涉及除法,如公式 2 所示。
![]()
重写公式 2 以避免除法需要两个乘法器,
如公式 3 所示。两种情况都需要比较器。
消除除法运算可显着节省 FPGA 资源。在 8 位输入的情况下,必须对大于 16 位的被除数和除数进行除法。这是因为计算需要多次平方和累加运算,每都会导致位增长。除法的消除也使得单周期吞吐量的实现相对简单。这些特性使该技术易于集成到实时信号处理系统中,特别是对于面积和时序受限的设计。公式 3 描述的设计框图如图1所示。
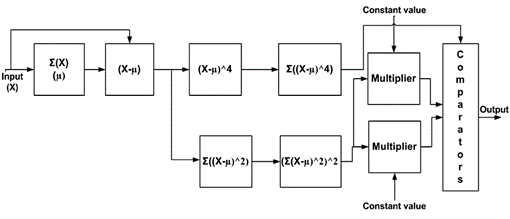
图 1 设计框图
如果窗口大小发生变化,可以通过更改 K 和 d 的预期值来扩展此想法以发现正态分布以外的分布异常。
通过提供 8 位纯高斯信号、具有脉冲干扰的高斯信号和正弦信号的数字样本,该设计在 Xilinx FPGA 上进行了测试。该设计是使用 Xilinx System Generator 创建的,使用 Virtex-5 FPGA 上大约 2% 的硬件资源来处理窗口大小为 1024 个样本的 8 位数据。该设计已经过高达 250 MHz 时钟频率的测试。使用除法器的设计将需要大约 8-10% 的 FPGA,并且会增加峰度计算的延迟。
乘法器块用作固定点,每个输入一个是常数(估计误差)。在乘法器块中添加的延迟由z -3 参数表示,表示三个时钟周期,添加该延迟是为了满足时序要求。乘数之后是一组比较器,用于检查峰度是否在规定的限制范围内。比较输出进行“与”运算以获得终输出。输出值“1”表示输入分布是高斯分布,“0”表示其他情况。
尽管该设计在基于 FPGA 的实时系统中作为检测器进行了测试,用于去除因干扰而损坏的样本,但它对于实施基于软件的峰度测试也很有效。
峰态计算在数字信号处理和数字通信领域的应用有:
去除无源微波辐射计高灵敏度通信接收机接收数据中的射频干扰。用于卫星有效载荷以消除脉冲干扰和调制 来自接收信号的干扰。
减轻射频干扰以提高射电望远镜接收器的灵敏度。它有助于消除由于电力线火花、汽车、通信发射机等引起的时域和频域脉冲干扰。
检测和去除由于时域和谱域信号中的脉冲干扰引起的非正态性。
查找数字通信接收器中接收信号的统计分布。这有助于在存在干扰的情况下测试接收器性能。
基于开关键控的调制中的能量和功率检测,对某些超宽带系统很有用。
系统间干扰的测量。










