0 引言

涡流检测技术是常用的无损检测技术的一种，能在不破坏被测试体的情况下检测其可能存在的缺陷，因此得到广泛应用。传统涡流检测通常采用圆柱形线圈，且检测线圈被包裹在激励线圈内^[1]，由于检测线圈同时受到激励场与涡流场的影响，降低了检测线圈的灵敏度。同时由于圆柱形线圈在导体上的感生涡流存在自抵消现象^[5]，故难以探测导体的信息。

而在矩形线圈的激励下，导体表面会产生一片同向流动的匀强涡流场，故不存在自抵消现象^[4]。并且改变了激励线圈和检测线圈的方位，激励线圈在上，检测线圈在下，且互相垂直。这样做的好处是检测线圈受到激励场的影响会变小，同时感生涡流的变化能够更好的体现在检测线圈上^[7]。

本文使用Maxwell 仿真软件对矩形线圈检测进行了仿真研究，并对缺陷信息做了定量分析，寻求缺陷信息与线圈检测信号幅值之间的数学关系。

1 涡流检测原理与仿真模型的建立

矩形激励线圈被放置在检测线圈的正上方，当给激励线圈加载正弦激励时，线圈周围会产生一个时变磁场，该磁场会先后穿过检测线圈和平板导体，并在导体表面感应出涡流。感生涡流会在线圈正下方一定区域内平行流动, 如图1 所示。当导体中存在缺陷时，会对感生涡流产生影响，检测线圈受到涡流场变化的影响会发生阻抗上的变化，从而实现对缺陷的检测^[3]。

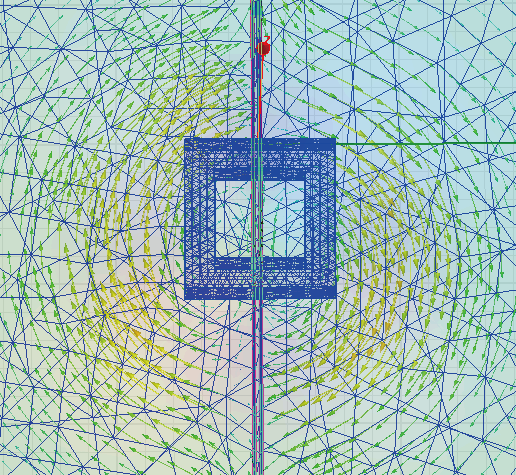
图1 感应涡流分布图

本文使用了Maxwell 建立了三维有限元仿真模型，采用的是自然网格剖分，在线圈和缺陷处剖分的较细，而在其他地方则剖分的较粗。如图2 所示分别为线圈和整体的剖分图。整个模型的参数如下：激励线圈内径为9 mm, 外径为15 mm，检测线圈内径2 mm，外径5 mm，平板导体的尺寸为100 mm×100 mm×25 mm，相对磁导率为1，电导率为1 300 000 Siemens/m 的金属导体，线圈均为铜制材料, 提离距离为0.2 mm。所加激励为幅值1 A，频率50 kHz 的正弦激励。

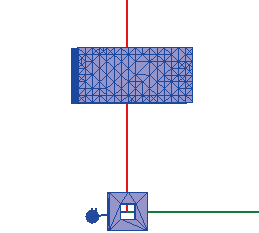
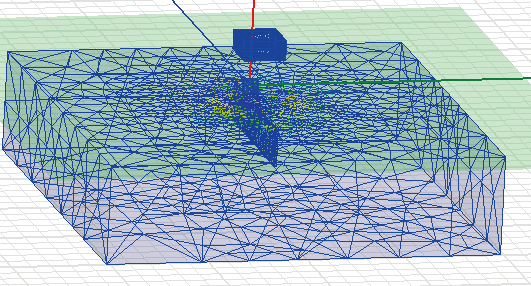
图2 线圈剖分图（上）和整体剖分图（下）

2 缺陷仿真实验

为了验证该模型能否探测导体的信息，在导体上挖了长40 mm，宽0.5 mm 的狭长矩形缺陷，并设置五个缺陷深度，分别为1、5、10、15、20 mm。检测线圈的提离距离设置为0.2 mm。

然后分别在不同深度缺陷下进行仿真实验，得到如图3 所示的检测线圈感应电压波形。通过对波形的观察可以发现，随着缺陷深度的加深，感应电压的幅值逐渐增加。由此可见，该模型能够探测较深层缺陷的信息。

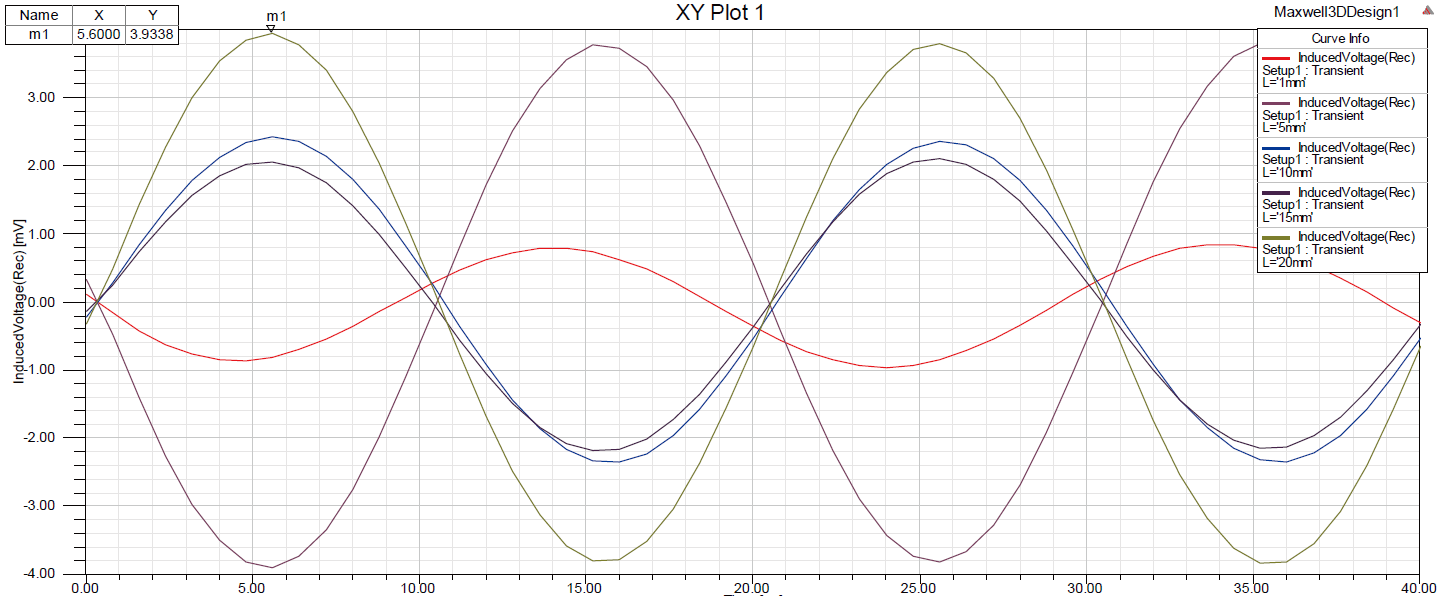
图3 不同深度下的检测线圈感应电压波形

3 定量化研究

3.1 采集信号峰值

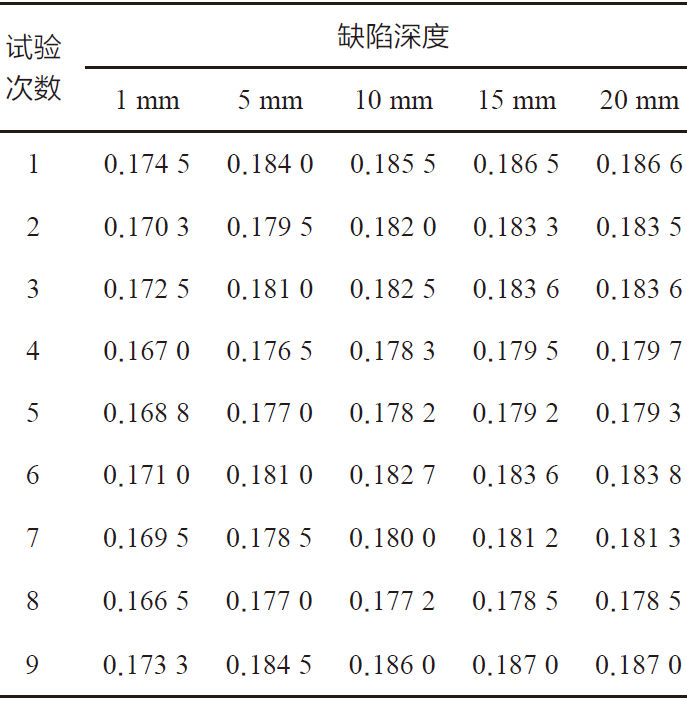
为了增加检测结果的可靠性，并且得到信号峰值与缺陷深度之间更具代表性的数学规律，在上述实验的基础上引进了俩个变量，即检测线圈的提离和位置。在保证单变量变化的情形下，分别对检测线圈提离为0.2、0.3、0.4mm，检测线圈位置分别位于缺陷正中心，左偏1 mm，右偏1 mm 时进行的仿真研究，得到9 组仿真结果，检测信号的幅值分别如表1 所示。

表1 涡流检测信号幅值（mv）

3.2 正态分布研究

假设所有变量对仿真结果的影响都是随机的，所以检测信号的幅值在一定范围内是一个随机数，同一深度的缺陷幅值满足正态分布^[2]，设x 为感应电压信号的幅值，正态分布的概率密度函数如下：

f(x)=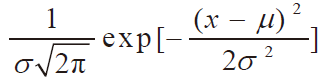   （1）

式中，μ 代表信号幅值的均值，σ 代表方差。

由正态分布的概念可知，信号幅值x 服从均值为μ ，方差为σ 的正态分布。选取概率密度峰值为最佳的检测结果，每次检测结果的幅值都会在该密度峰值左右一定范围内，并趋向于该密度峰值。所以选取概率密度峰值作为最佳检测结果，是比较合适的^[3]。

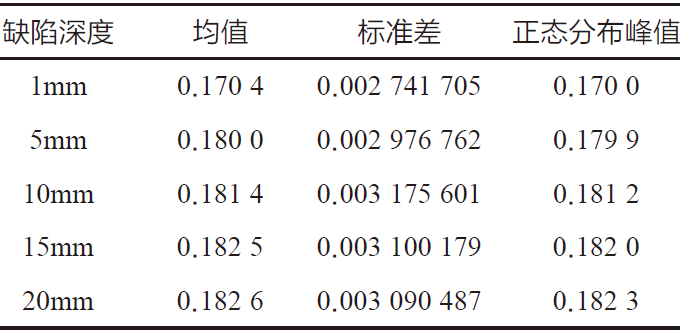
对表1 的数据进行均值和标准差的计算。然后根据算得的均值与标准差，使用python 的matplotlib 库可以快速的绘制幅值柱状图和正态分布曲线，如图4 所示，选取正态分布曲线峰值为最佳检测结果，并将该结果与均值、标准差共同绘制与表2。

图4 不同深度下的感应信号柱状图与正态分布曲线

表2 不同深度下信号的计算结果

3.3 多项式回归

通过对正态分布幅值的观察可以发现，正态分布幅值与缺陷深度之间并不是简单的线性关系。而多项式回归可以解决非线性问题，由于只有1 个因变量，故该回归问题为一元多项式回归，回归方程为：

y=b₀+b₁x+b₂x²+b₃x³+···+b^mx^m    （2）

当采用多项式进行回归预测时，阶数越高，拟合的越准确，但是随着阶数的加大，则会出现过拟合的情况，而阶数太低的话又会出现欠拟合的情况^[6]，所以寻找一个合适的阶数是很重要的。如图5 所示，分别是1 阶到6阶多项式拟合曲线，可以看到，阶数为4 时拟合的效果较好，也不存在过拟合。当阶数大于5 时，有一点过拟合。阶数为4 时的多项式为：

y=−8.76e⁻⁷x⁴+4.438e⁻⁵x³−7.867*10⁻⁴x²+5.958*10 ⁻³+0.1648   （3）

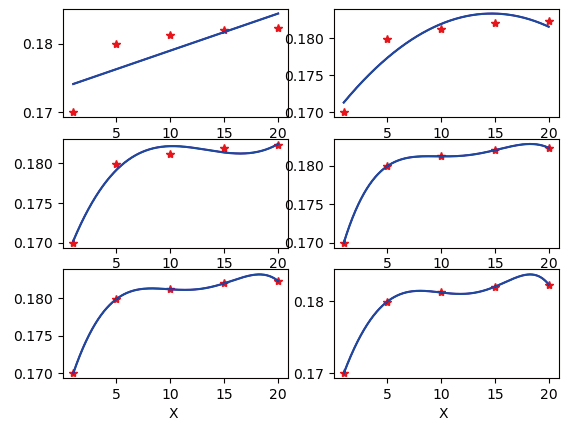
图5 1阶到6阶多项式拟合曲线

4 定量化方法应用

经过定量化研究得到检测信号幅值与缺陷深度之间的数学关系为y=−8.76e⁻⁷x⁴+4.438e⁻⁵x³−7.867* 10⁻⁴x²+5.958*10⁻³ +0.1648，为了验证该公式的准确性，对缺陷深度为4 mm时进行了仿真分析，结果如图6，信号的幅值为179.098 μV，即0.179 0 mV。将x = 4 带入式中计算， 可以得到信号幅值结果为0.178 7 mV。

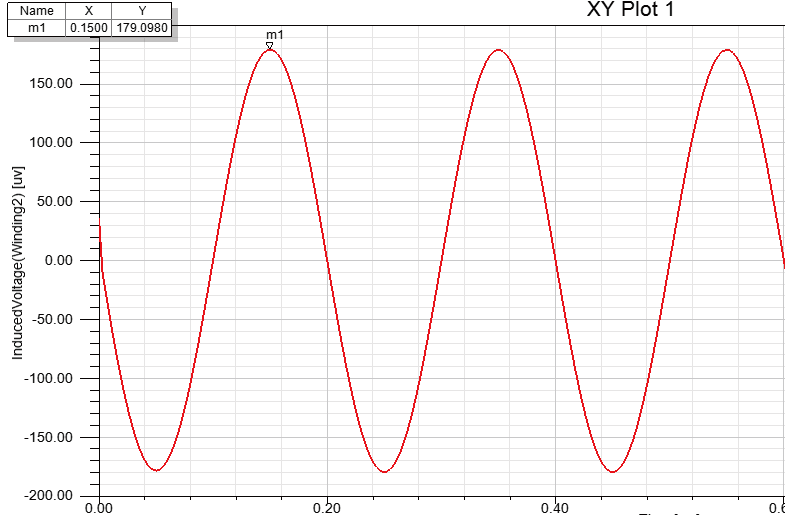
图6 4mm深度缺陷感应电压波形

5 结束语

本文使用Maxwel仿真软件进行矩形线圈涡流仿真，验证了该模型能够探测导体深层缺陷。并利用多次试验得到的检测信号幅值，绘制正态分布图，选取正态分布曲线的峰值为最佳检测结果。采用多项式回归拟合最佳检测结果与缺陷深度之间的数学规律，在多项式达到4阶时拟合效果较好，能够为预测缺陷深度提供一定的参考。

参考文献：

[1] YUSA N, Y SAKAI, H HASHIZUME. An eddy current probe suitable to gain information about the depth of ne ar-side flaws much deeper than the de pth of penetration[J].NDT & E International, 2 011,44(1): 121-130.

[2] 陈新波,等, 基于数理统 计的缺陷涡流检测定量方法[J].无损检测, 2020. 42(3) : 50-53.

[3] 丁民翰.基于涡流的金属表面缺陷检测系统的研究[D].广州:华南理工大学,2017.

[4] 康志斌,等,矩形脉冲的缺陷仿真研究[J].传感器与微系统, 2012. 31(6): 38-41.

[5] 常祥.平板导体深层缺陷的涡流无损检测方法研究[D].无锡:江南大学,2018.

[6] 李林凯.涡流无损检测中缺陷的定量研究[D].南京:南京农业大学,2017.

[7] 郭锐,等.用于电力管道缺陷定量分析的涡流检测技术[J]. 自动化仪表, 2016. 37(5): 4-9.

（本文来源于《电子产品世界》杂志2023年8月期）