
说到电子产品,有三个基本元件: 电阻器 、 电容器 和 电感器 。我们已经讨论过它们,并介绍了它们背后的基本工作原理。众所周知,电容器是电子产品的基本元件,对于存储和释放能量至关重要。您会发现它们用于各种用途,从解耦到滤波器,甚至作为新型 超级电容器 的备用电源。其操作的一个关键方面是 电容器充电时间 ,这是许多应用中的关键因素。在本文中,我们将研究电容器充电时间及其计算方法。
电容器充电时间 - 基础知识
我们知道,电容器连接到电源后需要一些时间才能充电。由于所有电路中都存在某种电阻,无论是连接线的电阻还是电池等电源的内部电阻,我们总是可以认为电阻与电容器串联。下图显示了一个简单的 RC 电路,其中电阻器 R 可以被视为实际电阻器或来自电线和电源的电阻。现在,我们的电容器 C 的充电时间取决于电阻器 R 的值。
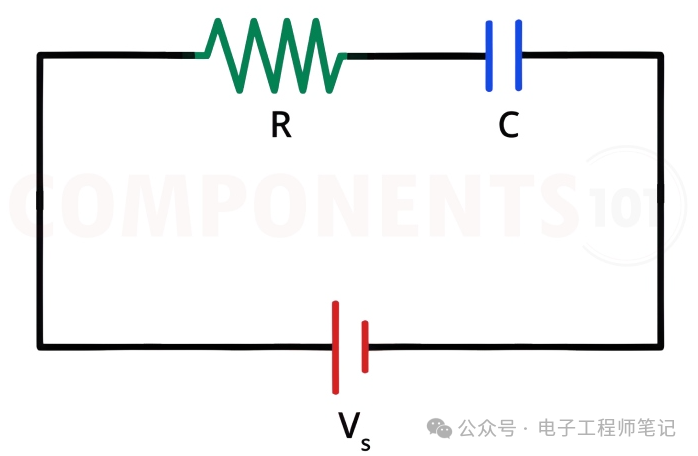
因此,电容器的充电时间主要由 电容器充电时间常数 决定,该常数表示为?(发音为 tau),它是电路中的电阻 (R) 与电容器的电容 (C) 的乘积。电容器充电时间可以定义为通过电阻器将电容器从初始充电水平零电压充电到施加的直流电压的 63.2% 所需的时间,或通过同一电阻器将电容器放电到其最终充电电压的约 36.8% 所需的时间。 电容器充电时间公式 可以表示为:
=RC
在哪里:
? (tau) 是时间常数,单位为秒。R 是电阻,单位为欧姆 (Ω)。C 是电容,单位为法拉 (F)。
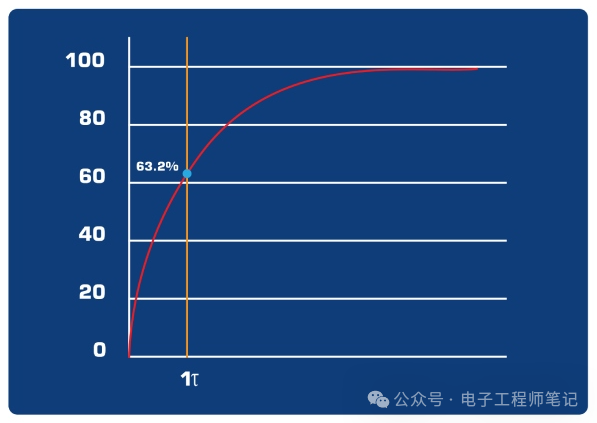
下面是 电容器充电时间图, Y 轴表示电压,X 轴表示时间常数 ? (tau)。如前所述,电容器充电至 63.2% 所需的时间为 1?,如下图所示。
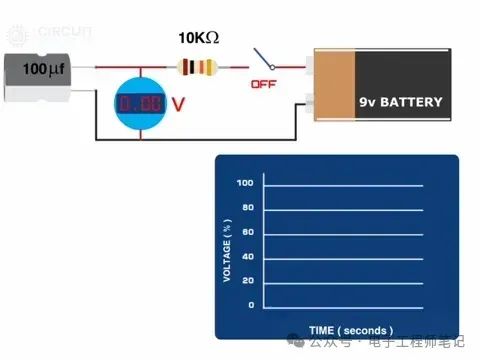
这是一个显示电容器充电的简单模拟。为了简化计算,我们为其添加了一个我们自己的串联电阻。 如果您想进行一些快速计算, 您还可以查看我们的 在线电容器充电时间计算器。
正如您在电压-时间图中看到的,电压一开始迅速增加,然后逐渐减慢,直到达到满电压。我们知道一个时间常数是电容器充电至满电压的 63.2% 所需的时间。所以我们用时间常数标记了 x 轴。从结果图中,您可以看到,当 5? 时,电容器充电至满电压的 99.3%。考虑到电容器在 5? 时充满电,我们可以使用以下电容器充电时间方程来计算电容器:
T = 5?= 5RC
例如,在上面的模拟中,我们使用了一个 100µF 电容和一个 10kΩ 电阻。因此,可以按如下方式计算电容充电所需的时间:
T=5RC = 50.000110000=5秒
即电容器将在5秒内充满电。
关于电容器充电时间的常见问题
给电容器充电的更快方法是什么?
我们知道,电容器的充电时间是时间常数的五倍,并且取决于电容和串联电阻。由于我们无法改变电容,因此下一个最佳选择就是最小化串联电阻。
电容器完全充电需要多长时间?
电容器永远不会充电至 100%。但您可以使用电容器时间常数计算电容器充电所需的时间,该常数通过将 R 和 C 相乘计算得出(tau = R * C)。电容器达到 99% 充电需要大约 5 倍的时间常数。电阻或电容越高,充电所需的时间越长
如果电容器直接连接到电池,则由于它们之间没有电阻,因此应该立即充电,因为根据上述公式,时间常数将为零。但事实并非如此。为什么?
理想情况下,电阻值为零,电容应立即充电。但在现实生活中,电阻值永远不会为零,我们需要考虑一些因素,例如连接线的电阻,电源的内部电阻等。
为什么当充电量只有 99.3% 时就将 5? 视为充满电水平?
正如您在 5? 图中所看到的,电压的增长率非常小,并且还在持续下降,将电池充电至 100% 需要无限的时间。
电容器可以充电 100% 吗?
实际上,将电容器充电至 100% 需要无限的时间。










