在本文中，我们将通过模拟设备的高频非理想性来了解变压器在射频应用中的局限性。

变压器在射频设计中执行许多有用的功能，包括：

阻抗匹配。

电路两部分之间的隔离。

平衡和非平衡信号环境之间的转换。

实现的方法有很多。最简单的方法是使用一对线圈。为了帮助增加线圈之间的耦合，这种变压器通常还包括一个磁芯。

图1显示了输入和输出端带有变压器的推挽式RF功率放大器。

在输入和输出端具有变压器的推挽式RF功率放大器。

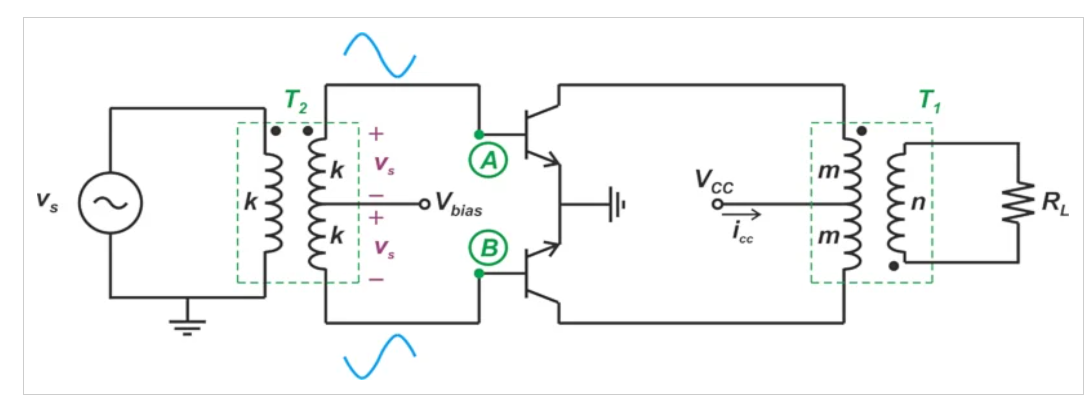
图1：变压器耦合推挽式放大器使用两个变压器来产生输入和输出信号。图片由Steve Arar提供

为了理解上述电路的局限性，我们需要了解实际变压器的非理想性。本文探讨了磁芯变压器在高频下表现出的主要非理想性。我们将从概述该变压器的理想版本开始。

理想磁耦合变压器

理想的变压器在初级和次级线圈之间提供完美的磁耦合，并且没有能量损失。图2显示了理想1：n变压器的示意图。注意极性点——这些点标识了哪些端子是同相的。

变压器原理图符号。

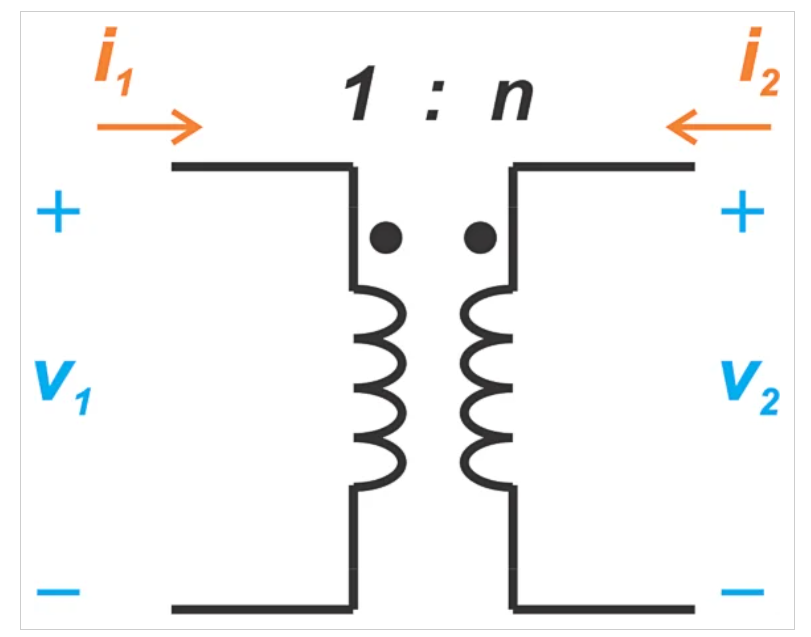
图2:变压器示意图。图片由Steve Arar提供

变压器点法规定了每个线圈相对于另一个线圈缠绕铁芯的方向。在图2中，根据点法，流入初级线圈点端的电流将从次级线圈点端流出。

根据图中所示的电压极性和电流方向，理想变压器的两个定义方程为：

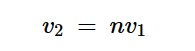
方程式1

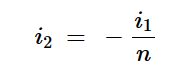
方程式2

哪里

i1是初级电流。

i2是次级电流。

v1是初级电压。

v2是次级电压。

方程式2中的负号是由于我们将i2绘制为图2中变压器虚线次级端子的输入。如果我们将i2绘制为离开点端子，则符号将为正。

磁耦合不完美

实际上，一个线圈产生的磁通量只有一部分与另一个线圈耦合。初级和次级绕组之间的耦合程度由互感（M）表征，如图3所示。

由两个具有互感的电感器组成的理想变压器。

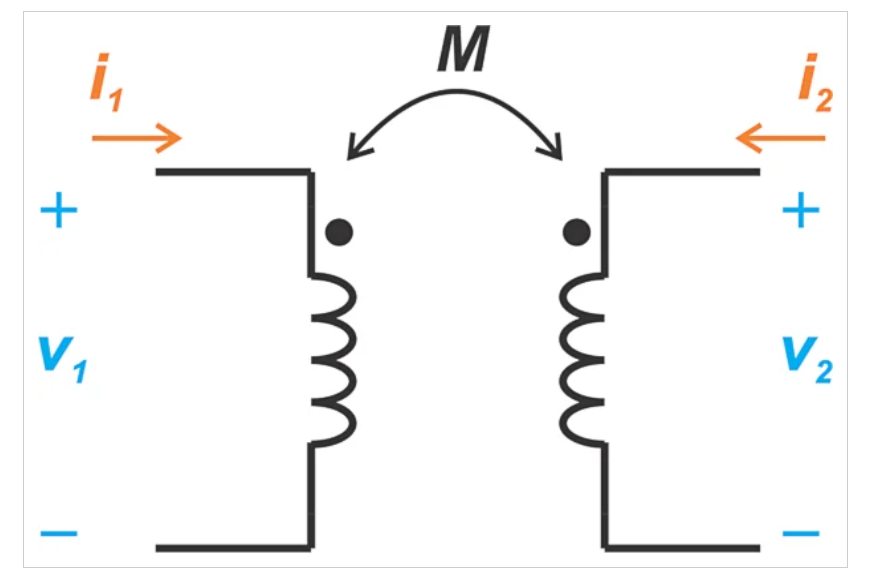
图3.由两个具有互感的电感器组成的理想变压器。图片由Steve Arar提供

线圈之间的磁耦合取决于以下因素：

线圈之间的间距。

线圈的取向。

每个线圈的匝数。

铁芯的磁性。

对于上述电路，初级和次级电压可以用以下相量方程表示：

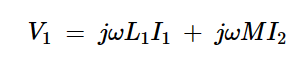
方程式3

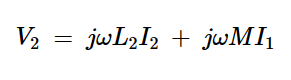
方程式4

哪里

L1是初级线圈单独的电感，次级线圈开路。

L2是次级线圈的自感。

M是互感，必须为正值。

根据点划线约定，如果电流被发送到耦合电感的点划线端子，则连接线圈的磁通量会增强线圈的自磁通。这就是为什么在方程3和4中，互感项被添加到自感项中。相反，如果一个线圈电流进入线圈的点划线端，而另一个线圈电流进入线圈的未点划线端，则我们从自感项中减去互感项。

磁耦合程度也可以通过耦合系数参数（k）来指定，其定义为：

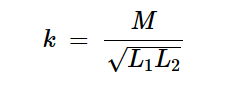
方程式5

M的最大值为

 $\sqrt{L_1{L}_2}$.

由于M必须具有正值，这意味着k的最小值为0，最大值为1。当k=0时，不存在耦合。

大多数电力系统变压器的k值接近1。由于大多数集成电路工艺中没有磁性材料，RF集成电路电感器的总耦合系数通常为0.8到0.9。

对变压器漏磁进行建模

图4使用图3中的理想变压器创建了一个有用的磁通泄漏模型。电感器Lpl和Lpm考虑了线圈之间的不完美耦合。

模拟变压器中的磁通泄漏。

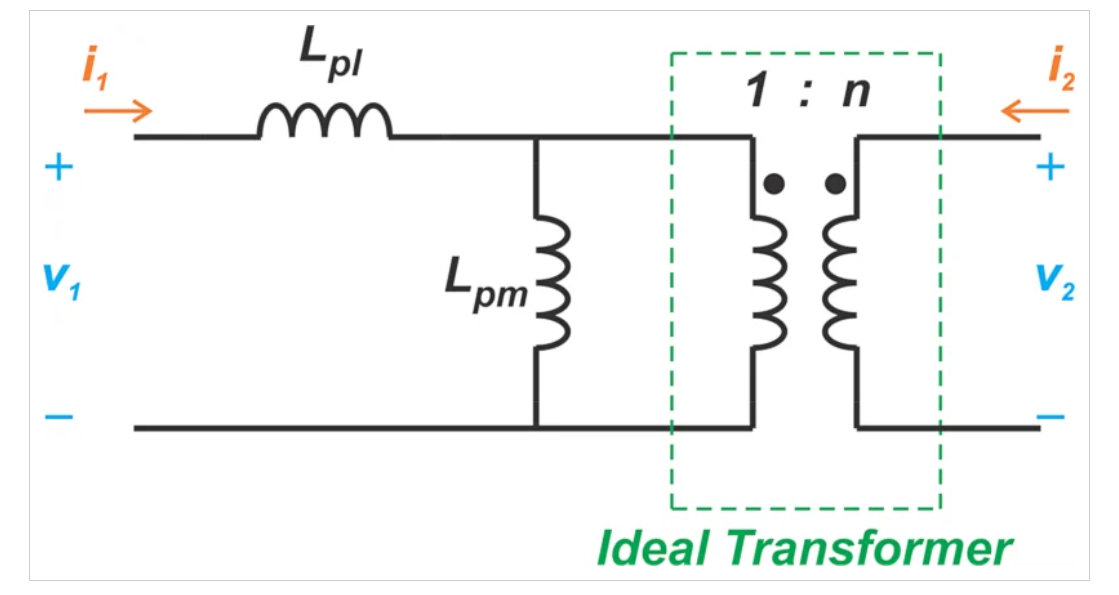
图4.变压器中磁通泄漏的建模。图片由Steve Arar提供

该电路的电压和电流量由方程2决定，两个电感器将总初级自感分为两部分。漏电感（Lpl）是不影响初级和次级绕组之间磁耦合的部分。磁化电感（Lpm）是影响线圈之间磁耦合的部分。

上述模型中的漏电感由下式给出：

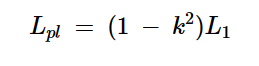
方程式6

磁化电感通过以下公式计算：

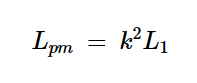
方程式7

最后，匝数比定义为：

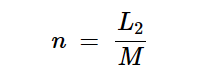
方程式8

变压器频率范围的下限

磁化电感提醒我们，现实世界的变压器不能在直流下工作——即使漏电感在低频下具有可忽略的影响，磁化电感也会缩短信号路径。该电感与驱动初级绕组的源电阻（RS）一起形成高通滤波器，截止频率为

$\frac{R_S}{L_{pm}}$

磁化电感的阻抗必须达到最小值，变压器才能正常工作。然而，只有当输入频率比截止频率高十倍左右时，阻抗才能达到这个水平。为了降低截止频率，我们必须提高绕组的电感。这增加了绕组的寄生电容，最终限制了变压器的高频响应。

主要核心损失机制

正如我们在文章前面提到的，磁耦合变压器通常包括磁芯。除了线圈之间不完美的耦合外，我们还需要考虑影响这些磁芯的两个主要损耗机制——磁滞损耗和涡流损耗。这些损耗会使传统的磁芯在高频下损耗极大。

交流信号在变压器上的应用会导致铁芯材料的磁畴发生振动。由于铁芯颗粒具有惯性和摩擦力，磁畴的运动会导致我们所说的磁滞损耗。在较高的频率下，铁芯的磁畴切换得更快，这就是为什么磁滞损耗随着信号频率的升高而增加的原因。电流的增加也会增加磁滞损耗。

一些磁芯材料是导体。当通过导电芯的磁通量发生变化时，它会形成小电流回路。这些电流回路称为涡流，产生与负载无关的功率损耗。涡流损耗与频率的平方成正比。

对变压器的损耗和非理想性进行建模

图5显示了包含几个非理想因素的变压器的更复杂的模型。铁芯损耗由与初级绕组并联的频率相关电阻（Rc）模拟。

具有非理想性的磁耦合变压器的等效电路模型。

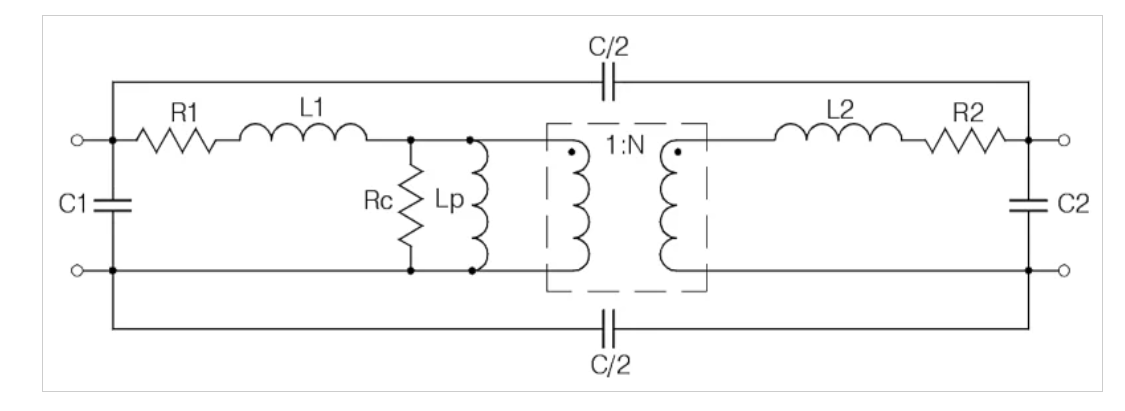
图5.具有非理想性的变压器的等效电路模型。图片由Mini-Circuits提供

上图，R1和R2模拟了初级和次级绕组的电阻损耗。由于趋肤效应，这些损耗项随频率增加而增加。它们也随温度增加而增加，在更高功率的应用中产生更高的损耗。另外，请注意，模型中存在串联电感（L2），以考虑次级绕组的漏电感。

存储在绕组之间的电场中的能量也会对变压器在高频下的性能产生不利影响。绕组需要彼此靠近以最大化耦合系数，这种接近会产生显著的寄生电容。大多数磁芯材料的相对介电常数大于1，进一步增加了这些电容。

图5模拟了以下寄生电容：

C1：初级绕组的寄生电容，其中可能还包括输入端的其他寄生电容。

C2：与次级绕组相关的寄生电容，称为绕组内电容或绕组的自电容。

C/2：匝间电容，表示两个绕组之间的电容耦合。

虽然在图5中寄生电容被建模为集总元件，但重要的是要记住它们实际上是分布式元件。图6说明了绕组间电容的分布式特性。

绕组间电容作为分布式组件。

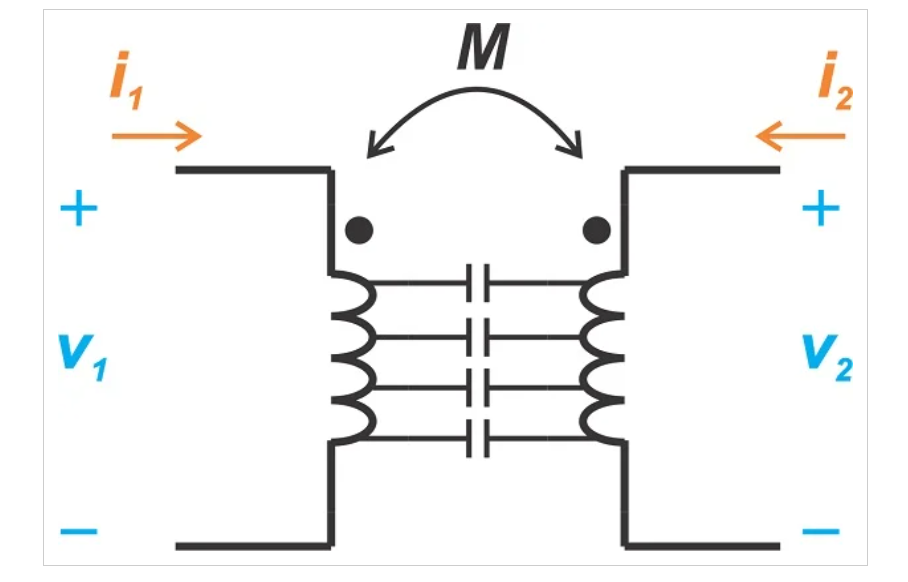
图6. 绕组间电容实际上是一个分布式组件。图片由Steve Arar提供

变压器频率范围的上限

漏电感和寄生电容决定了变压器的频率范围的上限。随着频率的增加，漏电感呈现的电抗也会增加，最终会阻挡信号。寄生电容在高频下呈现电抗减小。C1和C2使信号路径短路，绕组间电容绕过变压器。

更好的射频变压器

磁耦合变压器最适合低频应用。为了向上扩展变压器的频率范围，我们需要降低漏电感和寄生电容。这样做需要平衡相互矛盾的要求。

例如，我们可以增加绕组之间的物理距离来降低绕组间电容，但这会降低耦合系数，导致漏电感增加。我们可以通过使用磁芯来增加耦合系数，但磁芯的磁滞损耗和涡流损耗使其不适合高频。此外，一些射频应用需要相对较大的阻抗变换比，这需要具有极低漏电感的变压器。

幸运的是，这个问题有一个优雅的解决方案——我们可以使用传输线变压器。使用这种类型的变压器，绕组间电容和漏电感被假设为传输线的分布元件。在下一篇文章中，我们将看到如何将变压器的线圈视为传输线，使我们能够构建在射频和微波频率下成功运行的变压器。