均方根(RMS)噪声转换为峰峰值噪声的换算公式是：‌峰峰值噪声 = RMS噪声值 × 6.6。‌

这个换算公式基于一个假设，‌即RMS值等于标准差，‌且没有直流成分。‌在电子工程领域，‌特别是在处理运算放大器噪声时，‌这种转换尤为重要。‌例如，‌在处理仪表放大器噪声或同相配置运算放大器的噪声时，‌了解如何将RMS噪声转换为峰峰值噪声是非常关键的。‌这种转换不仅有助于理解噪声的幅度，‌还有助于评估系统对噪声的容忍度。‌

此外，‌这种转换在电路设计和分析中也很有用，‌尤其是在需要将1/f噪声从峰峰值转换为RMS时，‌可以通过除以6.6来实现。‌这种转换在估计噪声带宽和计算宽带噪声贡献时特别重要，‌尤其是在设计基准电压源电路时。‌通过这种方式，‌工程师可以更准确地评估电路的性能和可靠性，‌确保设计的电路能够满足特定的噪声要求。‌

《运算放大器参数解析与LTspice应用仿真》一书历时半年多完成撰写，目前出版准备工作也有序展开。该书的写作初衷是为模拟电子工程师在放大器设计和使用中，提供有效的指导与帮助，力争使本书成为工程师案头的常备参考书籍。

该书是笔者在整理放大器参数资料基础上，从所支持过的600余例项目中，精选十余项极具代表性的放大器设计案例，深入分析参数的应用。并且配合50余例LTspice仿真电路，以实际运算放大器的模型实现参数特性验证。该书还能帮助工程师熟练掌握LTspice仿真工具的使用，在日常工作中高效、可靠的保证项目 研发的进度，以及实现模拟电子工程师工作技能的提升。

一款单通道的放大器通常只有5个引脚，看似十分简单的器件，但是它作为模拟信号处理的核心器件，必须在应用中详细评估设计需求与放大器参数的匹配度。本篇文章 ，呈现放大器噪声RMS值的繁琐计算方式，以及使用LTspice仿真轻而易举实现噪声RMS值的有效评估。欢迎大家讨论，分享。

放大器的噪声

类型与分析

放大器内部的噪声由1/f 噪声与 宽带噪声组成。二者是不相关的，所以通过 均方根计算总噪声。

(1 )闪变噪声又称1/f 噪声。它普遍存在于自然界和人类的生活中，在放大器中主要与半导体晶体结构不完美有关，具有如下特性：

1)1/f 噪声随频率增加而下降

2) 每倍频(或十倍频)的带宽内包含相同功率。

放大器电压、电流的1/f 噪声RMS 值，分别为式2-51 、2-52 。

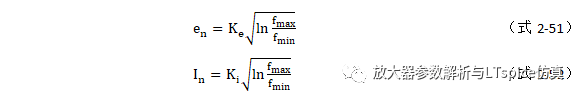
式中，e n ,I n 是测量到1/f 噪声RMS 值，K e ,K i 是比例常数，f max ，f min 是频带的上下限频率点。

(2 )宽带噪声，一个带宽内噪声功率为恒定值的噪声，即噪声密度为常数。宽带噪声、散弹噪声、电阻热噪声可近似认为是白噪声。之所以称为白噪声，因为与白色光有相近之处。在白色光中，所用的颜色都是等量。

放大器电压、电流的宽带噪声RMS 值，分别为式2-53 、2-54 。

其中e wn ，I wn ，分为电压噪声密度与电流噪声密度。

如图2.77 ，放大器噪声与频率特性，X 轴代表频率，单位为Hz,Y 轴代表电压噪声密度，或者电流噪声密度，单位通常为nV/ √HZ ，pA/ √HZ 。在低频率范围内，以1/f 噪声是总噪声主要成分，在高频范围内，以宽带噪声为总噪声的主要成分。将1/f 噪声曲线向高频延伸，宽带噪声向低频延伸，在二者的交点1/f 噪声与宽带噪声幅度相等，该点频率称为“转角频率”f nc 。该点的总噪声为√2 倍的宽带噪声。

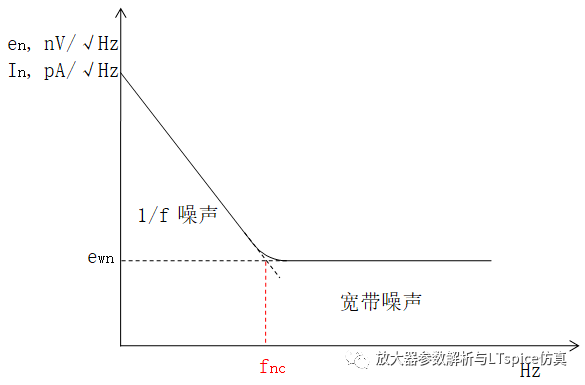
图2.77放大器噪声频率特性

fnc 的位置与总噪声计算相关，需要精确计算，步骤如下：

(1 )计算最低频率上的1/f 噪声的平方，将它减去宽带噪声平方的结果，乘以最低频率，即为该频率点1/f 噪声的平方值。

(2 )将最低频率点1/f 噪声的平方值除以宽带噪声的平方值，所得结果为f nc 。

【 放大器电压噪声计算示例】如下以 ADA4077的电压噪声为例，使用1/f噪声密度与宽带噪声密度，计算1Hz~1KHz总噪声的RMS值。

如图2.6 ，ADA4077 在1Hz 处电压噪声密度为13nV/ √Hz ，在1KHz 处电压噪声密度为6.9nV/ √Hz 。1Hz 可视为电压1/f 噪声的最低频率，1KHz 的噪声可视为宽带噪声，计算转角频率。

图2.6 ADA4077噪声与隔离度性能

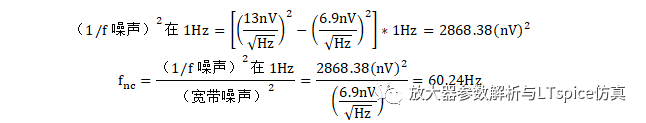
将转角频率、1/f 噪声密度、宽带噪声密度代入式2-51 、2-53 ，可以计算1Hz 至1KHz 的总噪声RMS 值为：

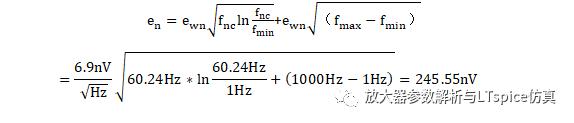
放大器电路的

噪声分析

在放大器工作电路中呈现的总噪声是包括电流噪声、电压噪声、电阻噪声。 首先需要根据实际电路分析得到主体噪声因素，然后将主体噪声因素的影响视为总噪声近似评估。

【 放大器电路噪声分析示例】如图 2.78 ，当信号从A 点引入，电路视为反相放大电路，增益为-R 2 /R 1 ，当信号从B 点引入，电路视为同相放大电路，增益为1+R 2 /R 1 ，而噪声增益都为1+R 2 /R 1 。电路折算到输入端的总噪声RMS 值e n_RTI 为式2-55：

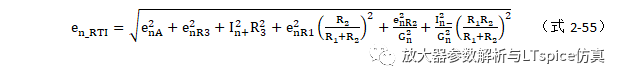
其中，e nR1 、e nR2 、e nR3 为电阻R 1 、R 2 、R 3 的热噪声，e nA 为放大器的电压噪声，I n+ 、I n- 为放大器的同相、反相输入端的电流噪声。在均方根计算中I n- 、e nR1 、e nR2 项的影响可以忽略，折合到输入端的总噪声RMS 值近似为式2-56 。

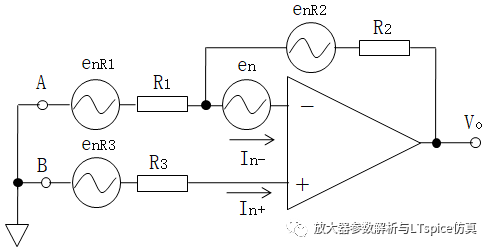
图2.78放大器电路噪声模型

如式 2-56 ，通常优先考虑电压噪声密度的影响。电流噪声密度为 pA/ √ Hz通常 比较小，只有当 R 3 电阻值大于 e n /I n (按宽带噪声密度计算)时，电流噪声的影响才能体现，否则电流噪声的影响可以忽略。只有电阻 R 3 的 阻值接近 e n /I n (按宽带噪声密度计算)时， R 3 热噪声的影响比较明显。

如图2.79 ，ADA4807 在25 ℃环境中，±5V 工作电压时，100KHz 处的噪声视为宽带噪声。电压宽带噪声为3.1nV/ √Hz ，电流宽带噪声为0.7pA/ √Hz ，所以当R 3电阻远小于4.4KΩ 时，电压噪声为主要成分，R3 电阻为4.4KΩ 时，热噪声为主要成分，当R3 电阻远大于4.4KΩ 时，电流噪声为主要成分。数据手册另外提供电压1/f 噪声转角频率为29Hz, 提供电流1/f 噪声转角频率为2KHz 。

图2.79 ADA4807 电流噪声与电压噪声

使用ADA4807 实现图2.78 放大电路，电阻R 1 为100 Ω, 电阻R 2 为900 Ω，分别设置R 3 的阻值为0Ω 、4.4KΩ 、440KΩ 计算电路的总输入噪声。其中，10Hz 为1/f 噪声的最低频率点，100KHz 的噪声为宽带噪声，评估各种状态下输入端噪声密度，如表2.8 。

表2.8 源阻抗R3对主要噪声的影响

依据表2.8 三种情况，分别计算电路总噪声，以及使用LTspice 进行噪声分析对比如下：

(1 )如图2.80 ，当源阻抗为0 Ω时，ADA4807 电压噪声为主体影响因素，折算到输出的噪声为：

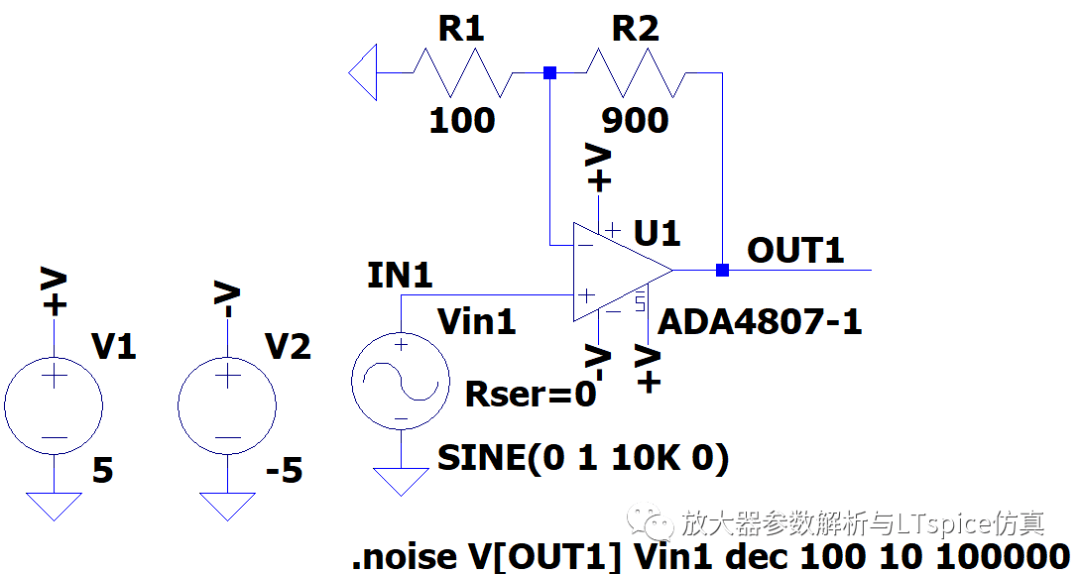
图2.80 源阻抗为0Ω 的噪声仿真电路

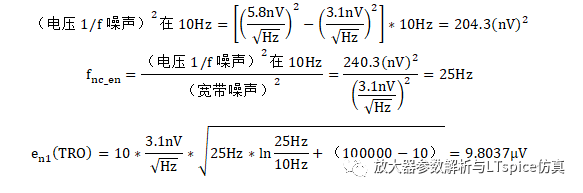
通过计算 电压噪声的转角频率为 25Hz与图2.79数据手册提供的29Hz接近，当源阻抗为0Ω时,ADA4807在10Hz至100KHz内，所产生的输出噪声电压RMS值约为9.8037uV。

噪声仿真结果如图2.81 ，输出噪声电压RMS 值为10.27uV ，ADA4807 电压噪声的影响约为95% 。

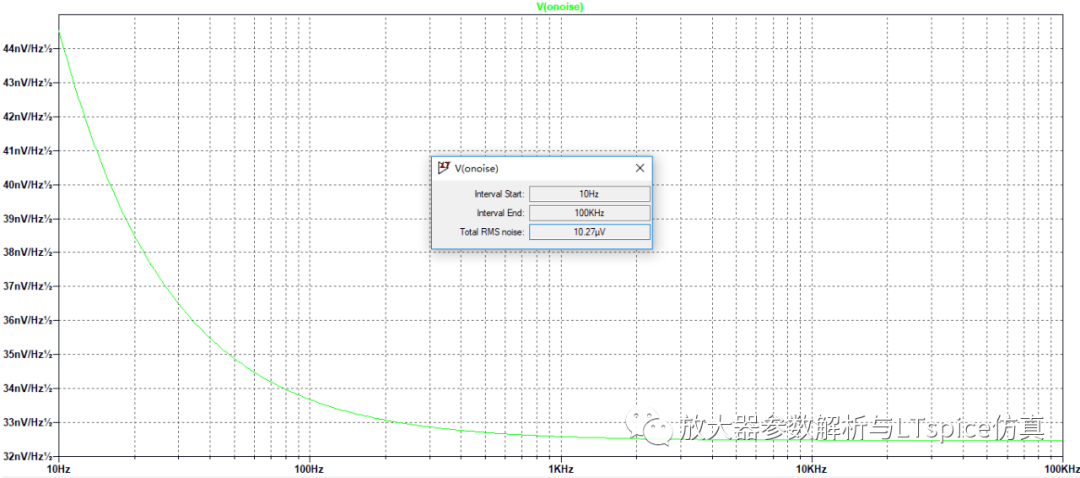
图2.81 源阻抗为0Ω时ADA4807输出噪声仿真结果

(2 )如图2.82 ，当源阻抗为440K Ω时，电流噪声为主体影响因素，折算到输出的噪声为：

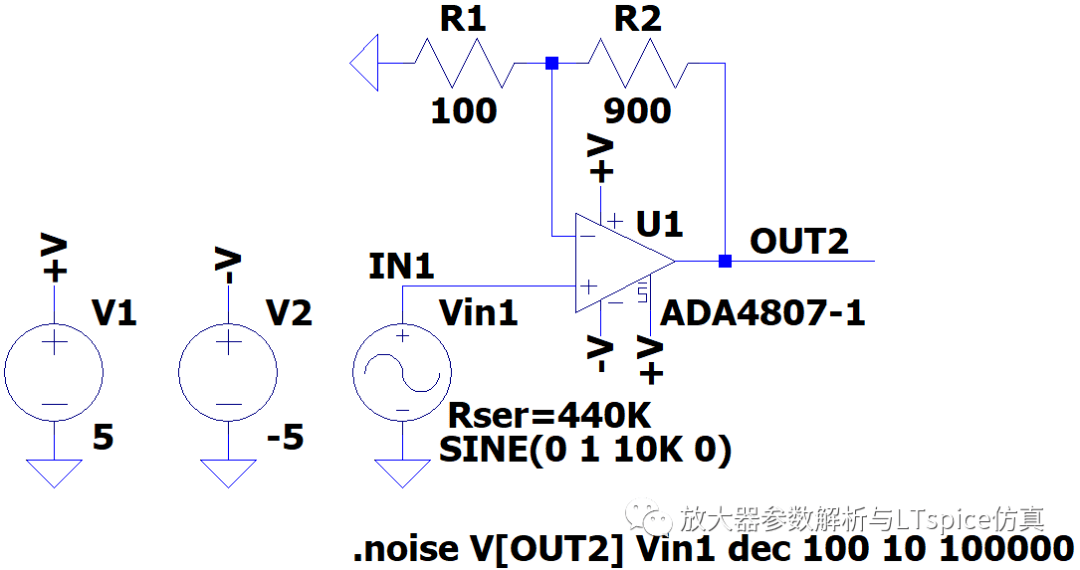
图2.82 源阻抗为440KΩ 的噪声仿真电路

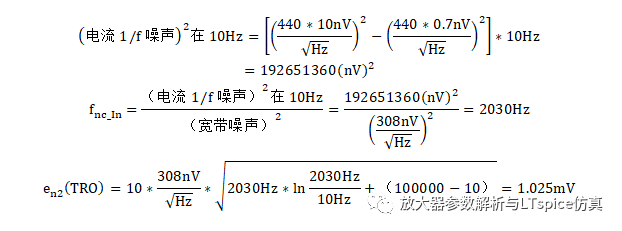
计算 电流噪声的转角频率为 2030Hz与图2.79数据手册提供的2KHz近似，当源阻抗为440KΩ时,ADA4807在10Hz至100KHz内，所产生的输出电压噪声RMS值约为1.025mV。

噪声分析结果如图2.83 ，输出噪声RMS 值为1.0557mV ，ADA4807 电流噪声的影响约为91% 。

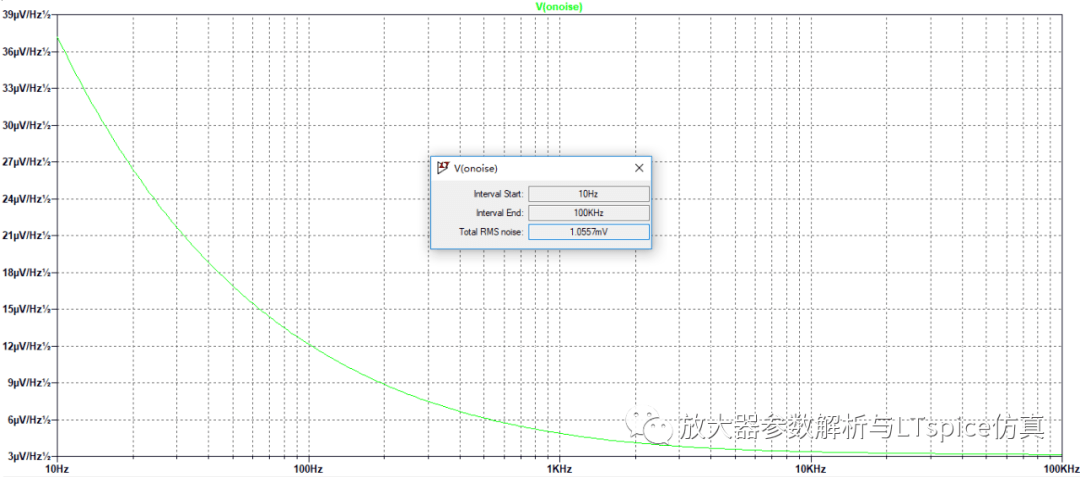
图2.83源阻抗为440KΩ时ADA4807输出噪声仿真结果

(3 )如图2.84 ，当源阻抗为4.4K Ω时，电阻的热噪声为主体噪声，折算到输出的噪声为：

在10Hz 至100KHz 内，电阻热噪声所导致的输出噪声电压RMS 值为26.53μV 。

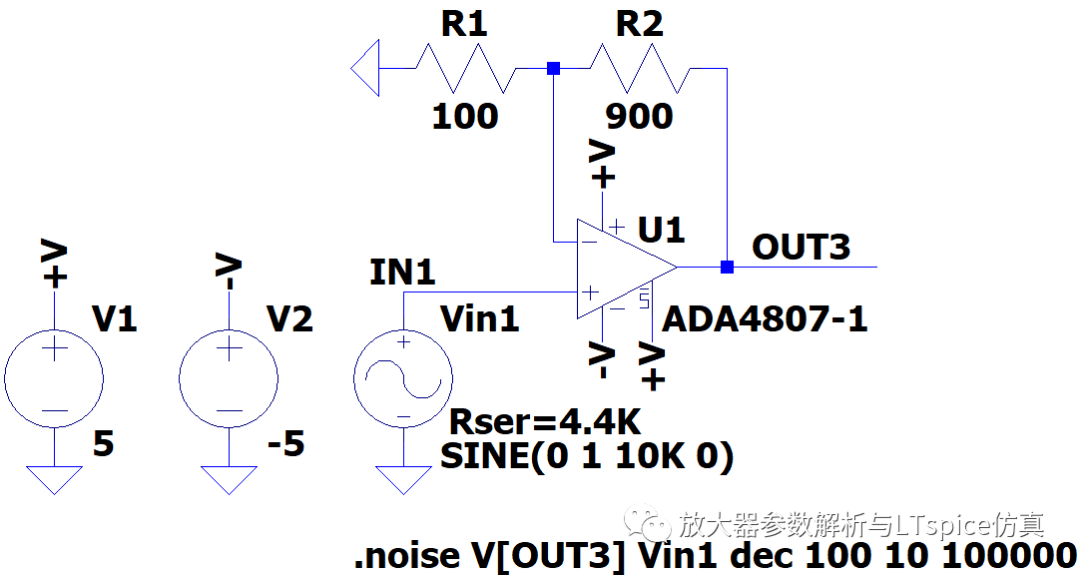
图2.84 源阻抗为4.4KΩ 的噪声仿真电路

噪声仿真结果如图2.85 ，输出噪声RMS 值为31.191μV ，电阻热噪声的影响约为85% 。

图2.85源阻抗为4.4KΩ时ADA4807输出噪声仿真结果

综上所述，在精密测量电路中应该控制电阻的阻值。单一主体噪声因素评估，适用于低源阻抗、和高源阻抗模式。对于源阻抗接近e n /I n (按宽带噪声密度计算)时，使用单一主体噪声因素评估，会导致的评估结果偏差增大。

通过仿真对理论计算的验证，更清晰掌握放大器电压噪声、电流噪声、以及电阻噪声在放大电路中的影响。在放大器电路噪声分析中，往往需要迭代多组配置参数，单纯依靠理论计算，即便排除人为因素导致误差，这样的工作量也不容忽视，所以能够使用LTspice 进行仿真无疑是最佳的选择。