由于运动单元只接受加速度和时间数字,因此PC的工作是计算它们。 由于我们的运动单元具有非常简单的架构和可预测性,这很容易做到。
本文引用地址:一点点数学
我们可以随时计算轴的位置和速度,只需知道加速度即可。
让我们为一个轴提供以下四个变量:
p 是位置
s 是速度
a 是加速度
t 是时间
我们还有增量变量:
Δ p 是增量位置(例如,如果位置 p 从 10 移动到 15,则 Δp 为 5)
Δs 是增量速度
Δa 是 delta 加速度
Δt 是增量时间
请注意,这是针对一个轴的。每个轴都是独立的,需要他自己的一组变量。
(离散时间)
第一个公式描述了轴在怠速开始时的行为方式,加速度为 1。
还记得硬件加速集成商页面中的表格吗?经过 5 个时钟,加速度为 1,表显示位置增加了 15。
公式为:
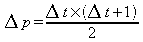
对于 Δt=5(5 个时钟),公式表示位置增加 (5x6)/2=15。好。
请注意,如果加速度大于 1,则结果是成正比的。因此,如果加速度为 10,则位置增加 150。
第二个公式描述了系统在恒定速度(无加速度)下的行为方式。

例如,如果 Δt=5(5 个时钟)且速度为 2,则位置增加 5x2=10。 当加速度为空时,速度保持不变。
第三个公式描述了速度如何受到加速度的影响。
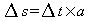
例如,如果 Δt=5(5 个时钟)且加速度为 4,则速度增加 5x4=20。
总之,这里有两个公式描述了给定加速度的位置和速度。
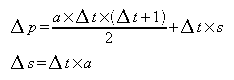
例如,如果当前位置为 200,速度为 10,加速度为 2,并且经过了 5 个时钟,我们现在处于位置 280,速度为 20。
(连续时间)
前面的公式适用于离散时间,即在中,一切都发生在时钟信号上(即使时钟非常快,也不像现实世界中那样连续)。
在现实世界中,时间是连续的。 然后一个公式略有不同(缺少 +1)。

为什么缺少 +1 可能令人费解。 一个线索是,由于时间是连续的,所以它是无限精确的,对于无限个数,加上一个有限的数是微不足道的。
单位
如果我们使用公制,我们可能有以下单位:
| 变量 | 单位 |
|---|---|
| p(位置) | mm(毫米) |
| s(速度) | mm/s(毫米每秒) |
| a(加速度) | mm/s²(毫米/秒/秒) |
| t(时间) | s(秒) |
在中,由于我们使用具有大量位的小数和高速计算,因此单位要小得多。例如,如果电机步进移动轴 0.01mm,位置寄存器的位 44 移动步进器,则位置表示精度为 0.01/(2^44) = 5.7e-16mm(比原子小得多)。
上一篇:
下一篇:
