0 1

基本概念

1.逻辑常量与变量： 逻辑常量只有两个，即0和1，用来表示两个对立的逻辑状态。逻辑变量与普通代数一样，也可以用字母、符号、数字及其组合来表示，但它们之间有着本质区别，因为逻辑变量的取值只有两个，即0和1，而没有中间值。

2.逻辑运算： 在逻辑代数中，有与、或、非三种基本逻辑运算。表示逻辑运算的方法有多种，如语句描述、逻辑代数式、真值表、卡诺图等。

3.逻辑函数： 逻辑函数是由逻辑变量、常量通过运算符连接起来的代数式。同样，逻辑函数也可以用表格和图形的形式表示。

4.逻辑代数： 逻辑代数是研究逻辑函数运算和化简的一种数学系统。逻辑函数的运算和化简是数字电路课程的基础，也是数字电路分析和设计的关键。

0 2

三种基本逻辑运算

与运算

1

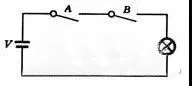
图1（a）表示 一个简单与逻辑的电路 ，电压V通过开关A和B向灯泡L供电，只有A和B同时接通时，灯泡L才亮。A和B中只要有一个不接通或二者均不接通时，则灯泡L不亮，其真值表如图1（b）。因此，从这个电路可总结与运算逻辑关系。

语句描述： 只有当一件事情（灯L亮）的几个条件（开关A与B都接通）全部具备之后，这件事情才会发生。这种关系称与运算。

逻辑表达式： L=A·B

式中小圆点“·”表示A、B 的与运算，又称逻辑乘。在不致引起混淆的前提下，乘号“·”被省略。某些文献中，也有用符号 ∧、∩表示与运算的。

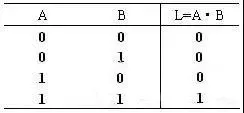
真值表： 如果开关不通和灯不亮均用0表示，而开关接通和灯亮均用1表示，得到如图1（c）所示的真值表描述。真值表的左边列出为所有变量的全部取值组合，右边列出的是对应于A，B变量的每种取值组合的输出。因为输入变量有两个，所以取值组合有22＝4种，对于n个变量，应该有2n种取值组合。

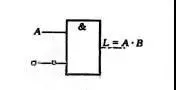
逻辑符号： 与运算的逻辑符号如图1（d）所示，其中A，B为输入，L为输出。

（a）电路图（c）用0、1表示的真值表

（b）真值表（d）与逻辑门电路的符号

图1 与逻辑运算

或运算

2

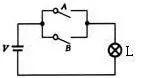
图2（a）表示 一简单的或逻辑电路 ，电压V通过开关A或B向灯泡供电。只要开关A或B接通或二者均接通，则灯L亮；而当A和B均不通时，则灯L不亮，其真值表如图2（b）所示。由此可总结出或运算逻辑关系。

语句描述： 当一件事情（灯L亮）的几个条件（开关A、B接通）中只要有一个条件得到满足，这件事就会发生，这种关系称为或运算。

逻辑表达式： L=A+B

式中符号“＋”表示A、B 或运算， 又称逻辑加，在某些文献中，也用符号∨、∪来表示或运算。

真值表： 同与运算一样，用0、1表示的或逻辑真值表如图2（c）所示。

逻辑符号 ：或运算的逻辑符如图2（d）所示，其中A，B表示输入，L表示输出。

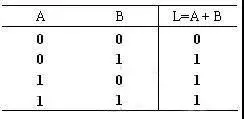
（a）电路图（c）用0、1表示的真值表

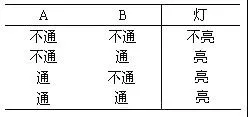
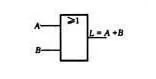
（b）真值表（d）或逻辑门电路的符号

图2 或逻辑运算

非运算

3

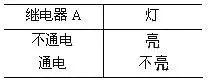
如图3（a）所示，电压V通过一继电器触点向灯泡供电，NC为继电器A的常闭触点，当A不通电时，灯L亮；而当A通电时，灯L不亮。其真值表如图3（b）所示。由此可总结出非运算逻辑关系。

语句描述： 一件事情（灯亮）的发生是以其相反的条件为依据。这种逻辑关系为非运算。

逻辑表达式描述： L=A

真值表： 若用0和1来表示继电器和灯泡状态，则可得图3（c）所示的真值表，在此图中，很容易理解，A不通电和灯不亮定义为0态，而A通电和灯亮是定义为1态。显然L与A总是处于对立的逻辑状态。

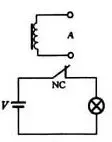
（a）电路图

（b）真值表

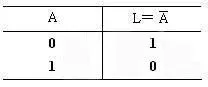
（c）用0、1表示的真值表

图3 非逻辑运算

式中，字母A上方的短划“－”表示非运算。在某些文献中，也用“～”、“┐”或“，”表示非运算。

逻辑符号： 非运算逻辑符号如图4（a）、（b）所示，其中图（a）为在输入端用小圆圈表示的非运算，图（b）为在输出端用小圆圈表示的非运算。

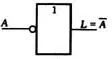
（a）在输入端用小圆圈表示非运算

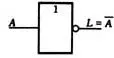
（b）在输出端用小圆圈表示非运算

图4 非逻辑门电路的符号

三种基本逻辑运算小结

4

与、或逻辑运算都可以推广到多变量的情况：

L=A·B·C…

L=A+B+C+…

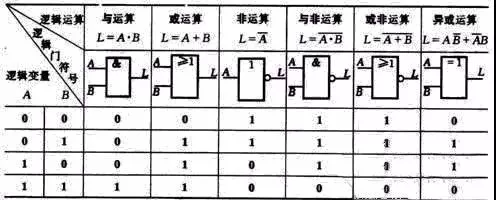
其它逻辑运算都可用上述三种基本逻辑运算组合而成。表1列出了几种基本的逻辑运算函数式及其相应的逻辑门电路的代表符号，以便于比较和应用。

部分电子书籍截图

【整套硬件学习资料合集】