在【精选知识讲堂】丨电感饱和与开关电源之间的密切关系，这篇讲透了！(上篇）中，我们揭示了电感饱和与开关电源之间的亲密关系，并从开关电源的控制模式开始，用各种数学方法分析了功率电感器饱和对开关模式电源控制运行的影响。

那么，纹波网络会给迟滞控制模式下的开关频率带来什么样的影响呢？我们利用R&S的一系列测试仪器（示波器、电源、探头等）搭建出了一套测试系统，使用不同的电感器测量功率变换器的纹波电流和开关频率，通过实验验证了上篇文章中各种数学算法的可行性。

纹波网络

使用去饱和电感器时，将电容和PCB中的寄生电感考虑在内，有益于迟滞控制的运行。还有一些迟滞控制的其他变体，引入了一些元件，在反馈控制信号中产生三角形纹波。在第一种情况中，在电容器种添加前馈电阻，这可以与具有极小ESR的陶瓷电容器一起使用。

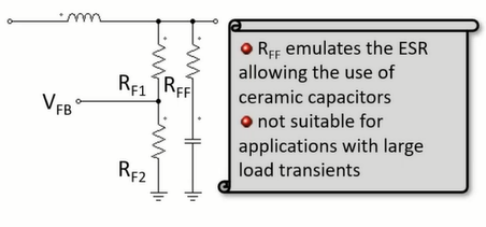
第二种情况下，添加一个电容器，一个与分压器电阻并联的前馈电容器。有助于提高开关频率。

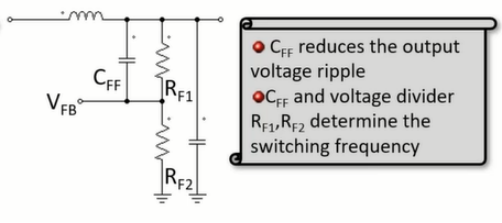
有几种可能的纹波网络解决方案，比如以下两个，增加了三个元件、和，利用功率电感器上的方波电压，在反馈信号上产生三角纹波。

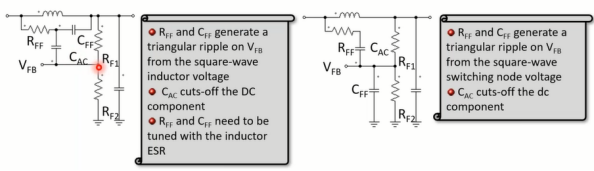
让我们看看其中一个解决方案的效果。例如，如果使用前馈加速电容器，如下图所示。

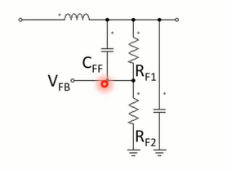
它对反馈信号产生的影响如下图所示，类似于电容器或印刷电路板布局中的寄生电感，由此得到开关频率表达式如下。

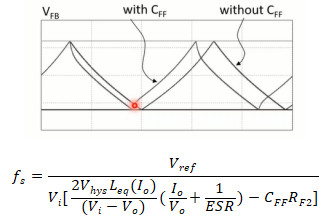
由此可见，开关频率有所增加。同样，从公式中可以看出，当调节器中有去饱和电感器时，较低负载时的开关频率会更低。较低负载时，效率会提升。而在最大负载时，没有任何效果。

以下左图是纹波网络的一个示例。注入迟滞比较器的反馈电压，是和两个信号作用的结果。这里的开关节点信号由RC高通滤波器提供。由此，可以得到三角形反馈信号。

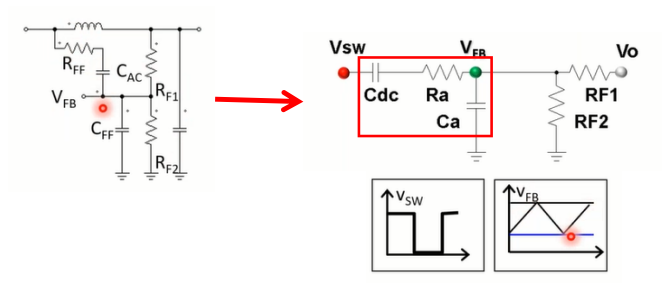
另一方面，输出电压仅作用于直流分量和可能的负载瞬态现象。

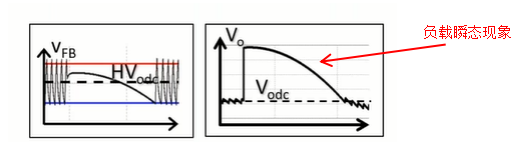
因此，开关频率由该附加纹波网络决定，而调节器输出由分压器决定。可以导出在该网络下开关频率和纹波的公式。

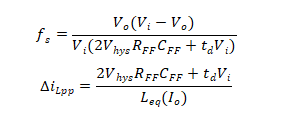
可以看到开关频率不再依赖于电感。事实上，这是使用纹波网络的主要目的之一，使开关频率独立于电感器和输出电容器的ESR。以便可以使用没有ESR或极小ESR的陶瓷电容器。但是纹波电流取决于电感器，因此，当在较低负载下运行时，可以减少纹波电流。

实验示例

基于功率电感器行为模型，以上所有模型的计算都是可实现的。可以先测量这些行为模型，然后应用适当的演变和人工智能算法生成类似的公式。对于上述讨论的迟滞控制功能的测试，可以使用TI-PMLK BUCK平台。

可以使用上图红色矩形所示两个部分，上半部分为迟滞控制器，下半部分为峰值电流模式控制器。在这个实验中，使用迟滞控制器部分。此外，还特别考虑了三种不同的功率电感器，这三个功率电感器中有两个尺寸相同（MSS7341-273和MSS7341-223），一个较大（MSS1038-183）为两个较小电感器体积的两倍。

本实验的目的是观察去饱和电感器的效果。这三种电感在饱和曲线方面有不同的特点，目的是使用这三个不同的电感器测量功率变换器的纹波电流和开关频率。

实验设置及结果

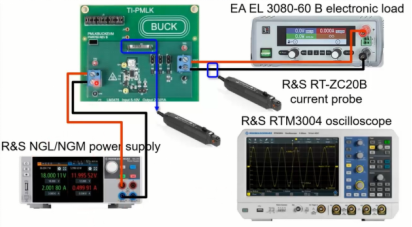
所使用的测量系统如上图所示，R&S NGL/NGM直流电源向电路板和EA EL 3080-60B电子负载提供能量，R&S RTM3004示波器的两个电流探头一个用于测量电感电流，一个测量负载电流。使用负载电流去触发示波器来分析变换器在负载瞬态条件下的特性。得到了三条不同的电感器饱和曲线。绿色代表尺寸最大的电感器，红色和蓝色代表两个较小的电感器。

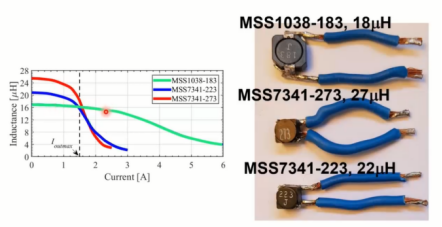
尺寸较大的电感器为18uH，相比于另外两个电感器，它的饱和电流更大。两个较小的电感器尺寸相同，但饱和度不同。在0.5A至1.5A的负载电流瞬态条件下，对该转换器进行的测试结果如下图所示。

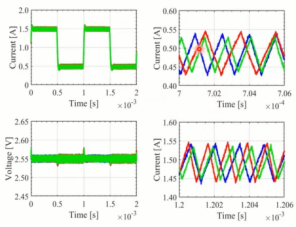
以上是仪器获取的数据导入MATLAB经过处理后得到的结果。较低电流0.5A和较高电流1.5A之间的差异显而易见。电流较高时，开关频率越高。通常情况下，与其他电感器相比，非饱和电感器的开关频率略高，但电感稍小。

当以较低负载电流工作时，可以明显看到饱和电感器的开关频率较小。27uH的最高标称电感器的开关频率更小得多。这证明，负载瞬态运行在开关效率方面是有效的，可以降低损耗。另一方面，该运行没有不良结果，也没有出现奇怪的现象。受迟滞控制功能的限制，纹波没有增加。所有元件之间的输出电压形状几乎相同。这证明使用饱和电感器没有问题。

峰值电流模式控制

峰值电流模式控制稳定条件

峰值电流模式控制是最流行的技术之一，利用电感器电流斜坡来替换或整合电压模式下的固定斜坡。

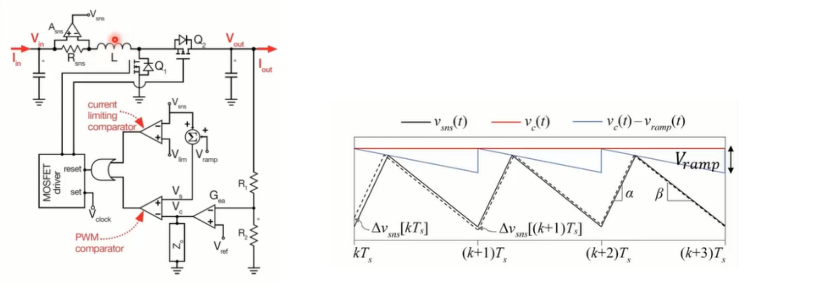
基本波形如上图左图所示，这个例子基本显示了线性电感器电流纹波从黑色曲线对应的稳定状态，过渡到扰动状态时会发生的情况。在红圈所示的某一点上，由于电源内部或外部任何变化，调节器的运行可能被扰动，电感电流也会受到扰动。我们希望在经过几个开关周期后，电感电流恢复到稳定状态，同时希望电流回路稳定运行。保证峰值电流模式控制器稳定运行的主要公式为

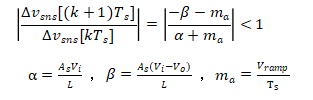
电感电流一个开关周期内两个子区间中的两个斜率α和β必须满足这个条件，其中是 的斜率。当电感器是线性电感器时，可以应用上述公式。

当电感器是饱和或去饱和电感器时，如下图黑色曲线所示，电感电流纹波的波形可能与线性电感器纹波的波形不同。

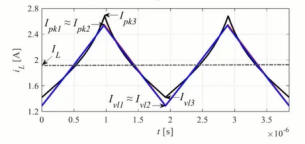
正常情况下，如果正确选择饱和电感器工作点，电感的变化很小。但为了证明在峰值电流模式控制中，使用饱和或去饱和电感器没有问题，考虑进行应力测试。

如下图为一个饱和电感器（电感变化曲线为黑色曲线），其特点是在开关周期内电感变化很大。如电流波形（黑色曲线）所示，电感电流的斜率在开始时较低，结束时较高。因为在开始时，对应电感曲线上，在结束时，对应电感曲线上。

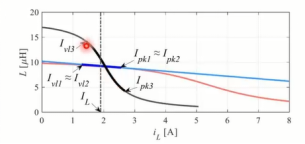
分析下图所示饱和电感电流的波形，可以发现，稳定条件与非饱和电感的情况相同。显然，电流的小于1。经过数学计算后，可以证明稳定性条件可以用与线性电感器情况相同的方式表示。即只需将两个子区间中电感电流的恒定斜率α和β替换为稳态运行中电流峰值的斜率。

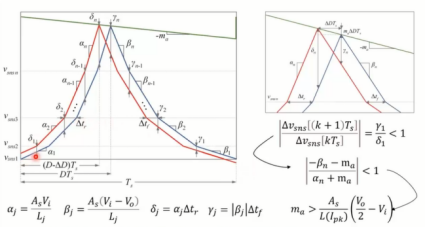
最终，得到了如下稳定性条件的公式。

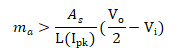
当使用饱和电感器时，应该用电感器在电流峰值时的电感值，而不是标称电感值。这个条件可以应用于任何类型的电感器——微饱和电感器或大部分饱和电感器。

下篇文章，我们将进行一个应力测试实验，利用R&S的一系列测试设备（示波器、电源、探头等）搭建一套测试系统，分别对负载和线路的瞬态应力，以及过流保护应力进行测试，验证选择饱和电感是否会让电路出现任何瞬态不稳定现象。