
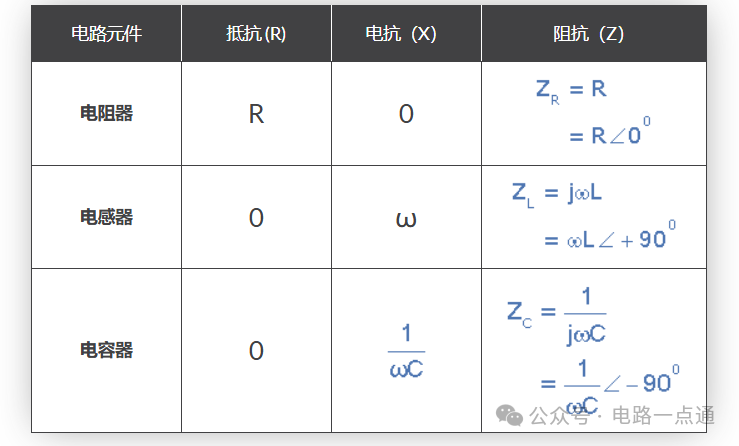
元件阻抗
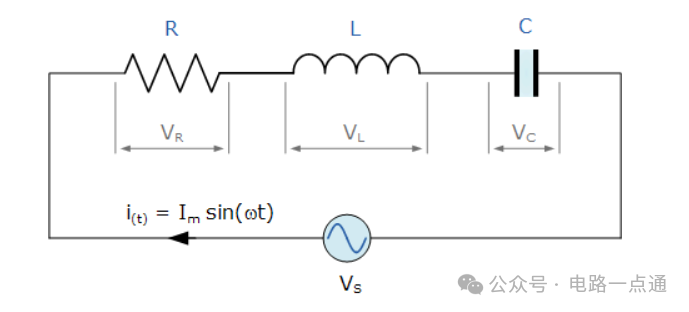
串联 RLC 电路
-
i (t) = I max sin(ωt) -
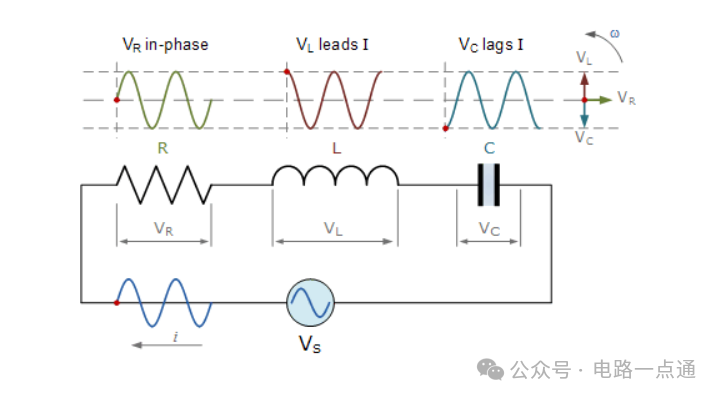
纯电阻两端的瞬时电压 V R 与电流“同相” -
纯电感两端的瞬时电压 V L “领先”电流 90 o -
纯电容器两端的瞬时电压 V C “滞后”电流 90 o -
因此, V L 和 V C 相差180 度 , 并且互相对立。
单独的电压矢量
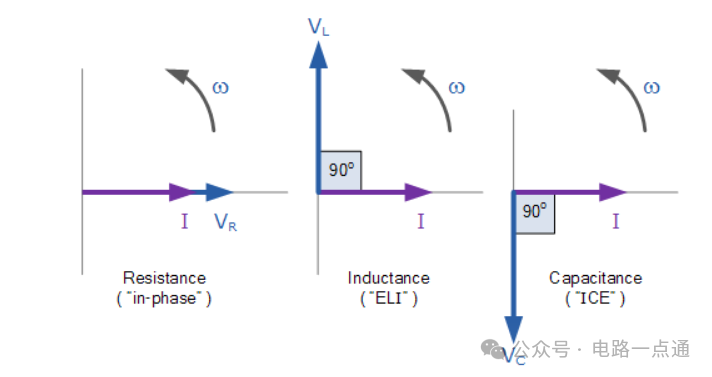
串联 RLC 电路的瞬时电压

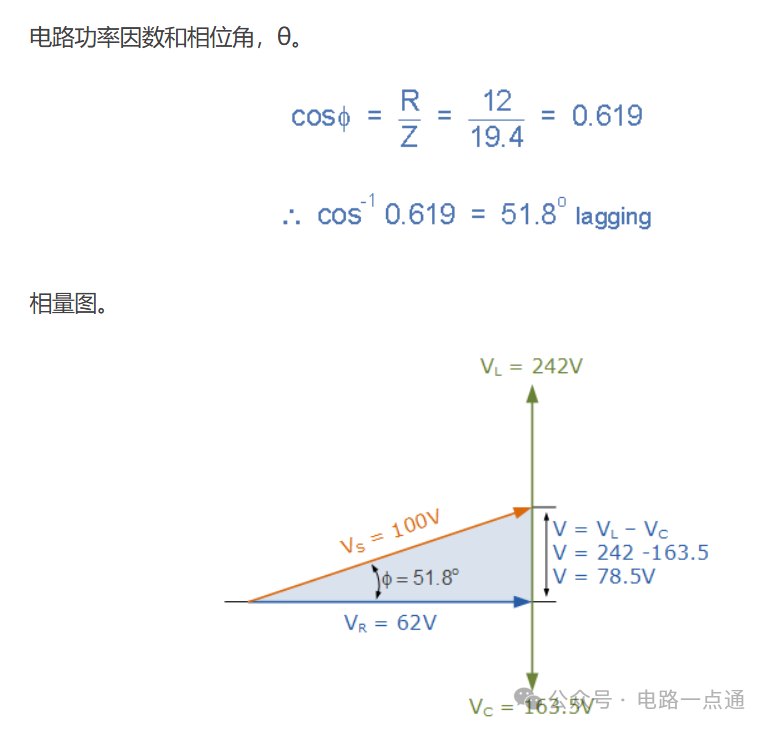
串联 RLC 电路的相量图
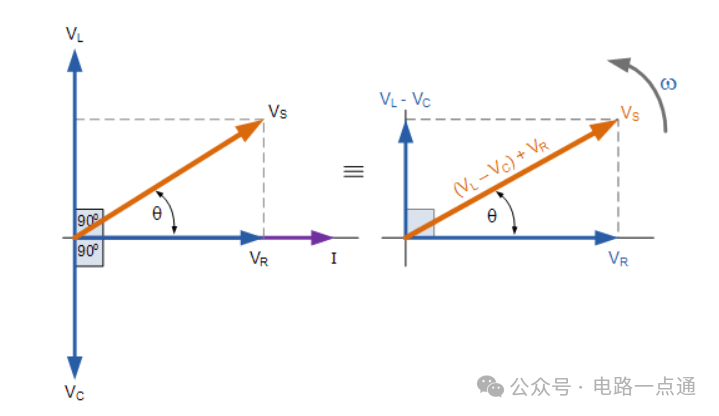
串联 RLC 电路的电压三角
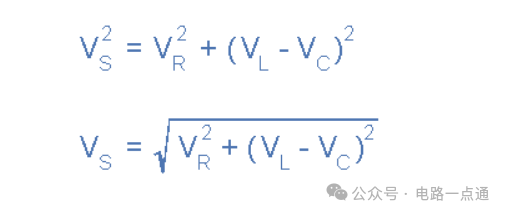

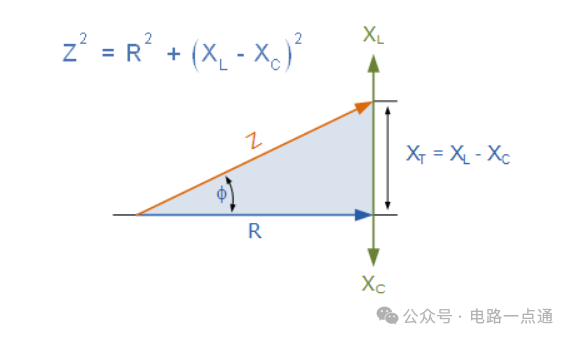
串联 RLC 电路的阻抗
串联 RLC 电路的阻抗三角

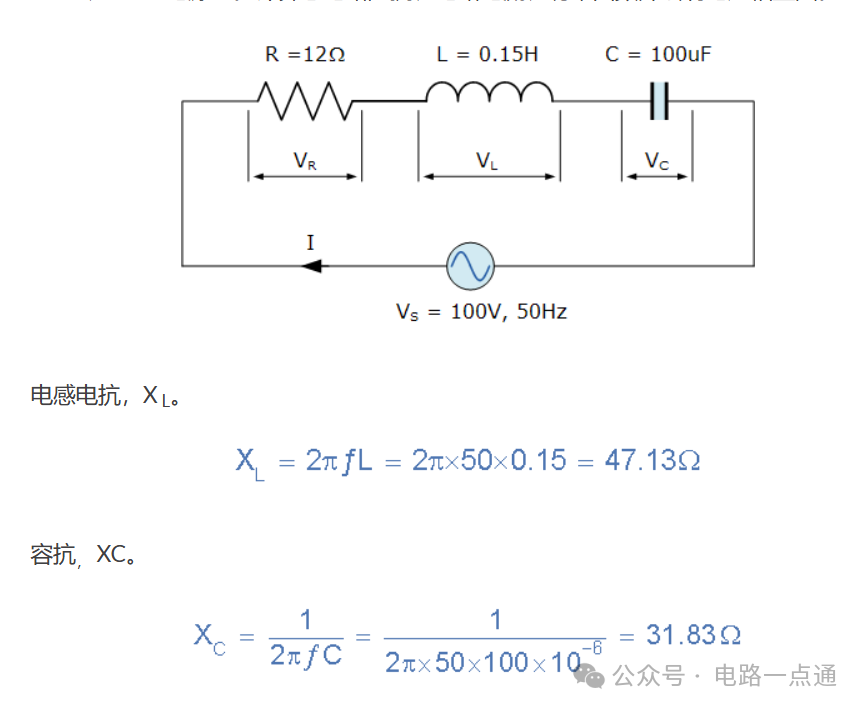
串联 RLC 电路示例 No1

文章来源于: 电路一点通
原文链接
本站所有转载文章系出于传递更多信息之目的,且明确注明来源,不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。










