随着自动驾驶技术的加速发展与应用落地，如何检验和验证自动驾驶车辆及系统的可靠性变得至关重要。自动驾驶系统存在的风险可以通过该系统发生事故即失效的概率衡量，因此，验证自动驾驶系统失效的概率是否低至可以接受水平是自动驾驶验证的一个重要目标。为了验证或估计这个极低的概率，需要高昂的时间及安全成本完成实车路测——根据相关分析，为了得到失效概率的一个可靠置信区间（95%置信度，相对误差20%）需要超过五千万英里的道路测试。故高成本效益的仿真模拟测试成为验证自动驾驶系统可靠性的重要手段。

本文简要阐述和分析蒙特卡罗方法面对小概率事件时的困难，如何通过可靠性分析算法估计自动驾驶系统在逻辑场景中的失效概率，并将基于场景的测试结果转化为整体失效概率。

01. 可靠性的定义

可靠性定义为被测试车辆或系统在某场景中不会失效的概率，即  。此处的失效是指被测试自动驾驶车辆及算法在一个具体场景中某项评价指标（kpi）小于阈值，即  ，其中  为该具体场景的参数值向量，  和  分别是评价指标函数向量和对应的阈值向量。为了便于说明，本文选取单kpi，多kpi的失效域可视为多个单kpi失效域的并集。

在此假设下，被测试自动驾驶车辆及算法在任意逻辑场景中失效的概率可定义为：

其中  是该逻辑场景中参数，  为这些参数的分布函数。

若逻辑场景  在  公里的平均出现频率为  ，则根据贝叶斯定理此被测试车辆或算法在  公里上的平均失效率为：

而车辆在  公里（或时间）上出现失效的次数一般被认为服从泊松分布，则 

通过仿真模拟，估计被测试车辆或算法在各逻辑场景中的失效概率  ，则该车辆平均在  公里上发生失效的概率可以估计为：   。

故如何构建估计量  ，正确稳定地估计被测试车辆或算法在各逻辑场景，即参数空间中的失效概率成为一个核心问题。

02. 估计量的好坏

在成本相同即采样数量相同的情况下，一个估计量  对真值  估计的好坏主要考虑准确性（accuracy）和精确性（precision）两个方面。

准确性衡量估计量是否能正确估计出被估计的真值，而精确性衡量估计量的散布范围。例如下图中，准确性描述弹孔是否以把心为中心，精确性描述单孔的散布范围，故①为精确而不准确，②为既不精确亦不准确，③为准确但不精确，④为即准确又精确。

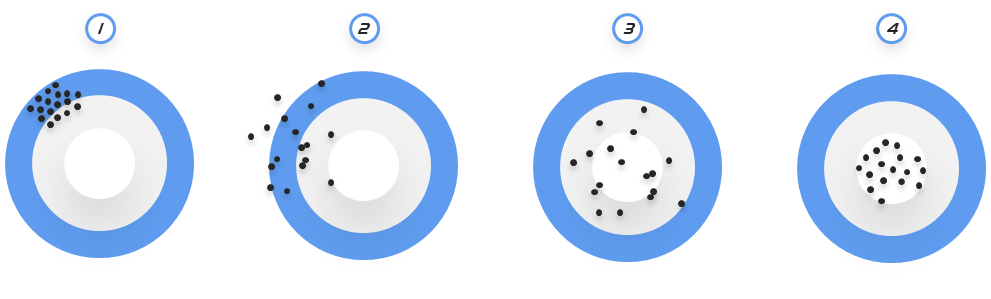
图1 准确性与精确性

衡量准确性的指标主要有偏差  及相对偏差  ；衡量精确性的指标主要为标准差  及相对误差（变差系数）  。   当  时我们称  为  的无偏估计；若  随着样本数量的增加趋近于0，则  为  的渐进无偏估计。仅当  的偏差较小时，讨论其精确性才有实际意义。

03. 朴素蒙特卡洛方法

对失效概率最简单的估计方式即朴素蒙特卡洛方法（CMC）。在测试空间中随机生成  个独立同分布的样本（场景），即  ,…,  ，其上车辆的表现函数为  。

即  为真值的无偏估计，同时其估计精准性不受测试空间维度影响，有着非常好的鲁棒性。当  趋近无穷时  依概率/分布收敛到的  的真值，其收敛性可由中心极限定理保证，即：   。   的相对误差/变差系数为：   。 通过上面的分析，我们无需担心  的准确性（其为无偏估计量）。其精确性即  由样本数  控制，并依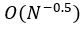的速度收敛。

04. 蒙特卡洛的困难

虽然传统蒙特卡洛方法有种种优势，但是当失效是小概率事件，正如现实情况中自动驾驶车辆及系统失效概率很低时，上述估计  的方法会陷入困难。

例如当自动驾驶系统或车辆在某测试空间中的失效概率为  ，为了得到较好的精确性，例如要求相对误差  ，则需要测试的具体场景个数约为  ，太多了！

因此，无法通过朴素蒙特卡罗的方法泛化并验证一个成熟的自动驾驶车辆或算法！虽然通过拉丁超立方或拟蒙特卡洛采样可以一定程度的节约成本，但即使  个测试场景依然是无法接受的。

05. 可靠性分析算法

根据上面的表达式可以看出，蒙特卡洛的困难的原因主要在于当失效概率很小时  的分母  过小。考虑  表示在  个随机场景中失效场景的平均个数，故一个自然的思路即通过增加采样中的失效场景个数来克服上面的困难，即应用一个更容易采集到失效场景的提议分布函数  来代替原始分布函数  进行采用，再通过下面的等式估计失效概率

其中  和  分别表示该逻辑场景中参数的原始分布及提议分布对应的密度函数。

赛目在测试空间分析工具中提供了基于此思想的自适应重要性采样、自适应splitting方法以及方向采样等可靠性分析算法，自动在测试空间中寻找失效临界，实现以可以接受的成本精确估计失效概率  。

图2 可靠性分析操作界面

为了说明可靠性分析算法的效率，下面的例子中我们选取了了一个显式的评价函数。

测试空间：  独立且服从标准正态分布；

评价函数：  ；

阈值：T分别取2、3、4、5。

下表列出对比了我们提供的自适应重要性采样与朴素蒙特卡罗方法在效率上的差异。

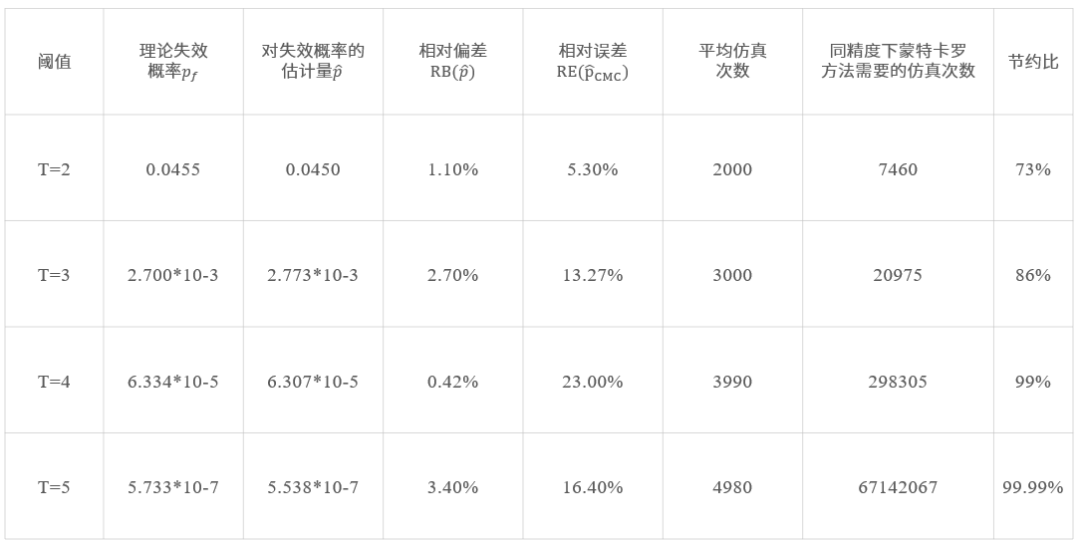
通过此例中的数据可以清晰看出，适合的可靠性分析算法可以准确估计失败概率（使用的自适应重要性采样实际为无偏估计），同时可以极大提升估计失效概率的效率，尤其时当失效概率较小时。例如次例中失败概率在  至  数量级时，同等精度下蒙特卡罗方法需要的仿真次数为十万至千万级，而实验中使用的可靠性分析算法只需要数千次仿真。并行仿真下，高效的可靠性分析算法可以大幅缩减时间成本，完成对自动驾驶车辆在多个逻辑场景中失效概率的准确估计。