永磁直流电机在控制中，经常要用到各种坐标变换，同时也会碰到各种电感，如：相电感、线电感、直轴电感、交轴电感、相间互感等，特别是电感和坐标变换结合后，就有不少人容易混淆迷惑。下面我们用图文及公式方式来理解直流电机电感其中的关系。

电感：1824年，奥斯特发现了电流效应，在通电导体周围的磁针会发生偏转，也就是电生磁，后来，法拉第和亨利发现了磁也能生电，在移动的磁场能会在导体中感应出电流，这就是现在所说的电磁感应，数学工程式为：

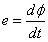
e：感应电压

dф/dt：磁通的变化率（单位Wb/s）

法拉第发表电磁感应论文不久，楞次发现了决定感应电流方向的规律，也就是楞次定律：感应电流的磁场总要阻碍引起感应电流的磁通量的变化，所以完整数学公式为：

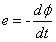
直流电机中控制中的自感与互感

在安倍定律中：磁场产生的根本原因是电流（可以是导体中的电流，也可以是永磁体中的电流）。如下图所示，一个线圈通电后，就会产生磁场

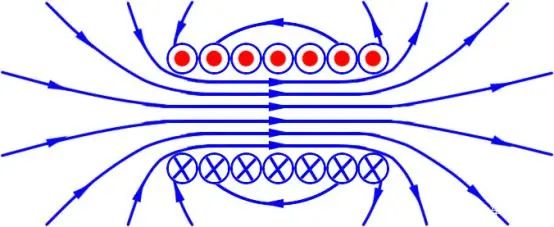
线圈本身就处于自身产生的磁场中，也就意味着线圈中也会产生磁通磁通，这个量对于我们来说不直观，也不好测量，既然磁通是由电流产生的那我们可以借助电流来表示，所以电感的定义是：

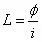
单位是Henry（亨利），一位美国物理学家，他其实和法拉第几乎同时独立的发现了电磁感应现象，只不过法拉第更早的发表了成果，就赢得了冠名权。

我们通常说的电感，严格来说应该叫自感，即线圈自己对自己产生磁通的能力。

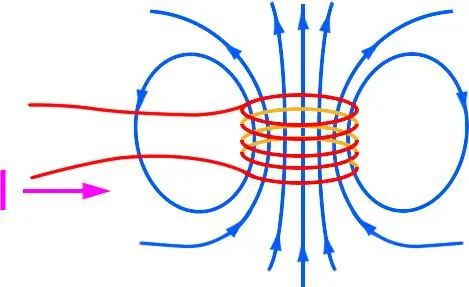
既然有自感，就会有互感，即两个线圈之间互相产生磁通的能力。

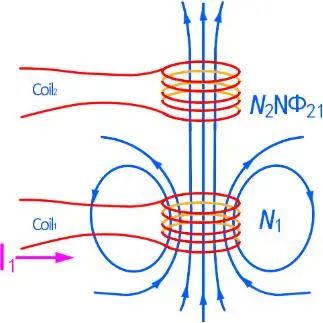
在直流电机中，电感非常重要，它表达了在某个特定机构中电流产生的磁场能力，电感确定了，我们就能很容易去研究磁场的性质。

什么是磁动势？

电感的定义是由磁通来定义了，要计算线圈的电感，先就要计算线圈通电后产生的磁场，由此来计算磁链，如，直流电机内磁路为线性，铁芯中的磁滞和涡流损耗可以忽略、气隙磁场的搞次谐波也可忽略，直流电机的定、转子表面光滑，齿、槽影响可以用卡式系数修正，直轴和交轴气隙可以不等，但是气隙的比磁导可以用平均值加二次谐波来表示

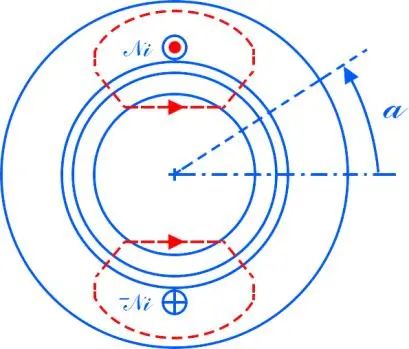
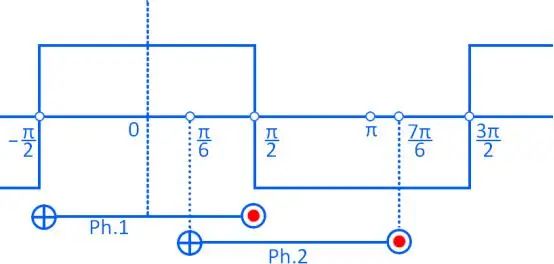
上图为直流电机定子槽内两极整距线圈的情况， ⊙为流出，为流入。根据安培环路定理，其磁动势分布图为：

磁动势的幅值为

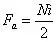
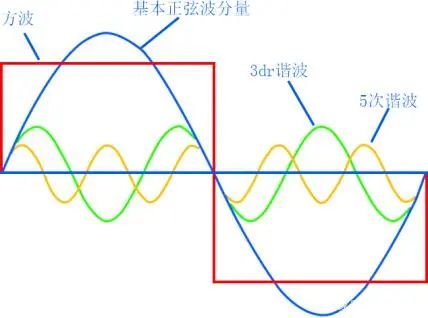
对方波进行傅里叶级数分析，可知其可由1、3、5，...等奇次谐波组成，其中1次谐波也称之为基波，其幅值为：

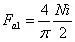
上面分析的是一对极情况，现在假设是p对极，每相绕组总匝数为Nph，则A相基波幅值为：

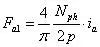
上面分析时绕组都认为是整距，且每极每相只有一个槽，实际电机很少这种情况，大多每极下面是多槽的，而且还是短距：

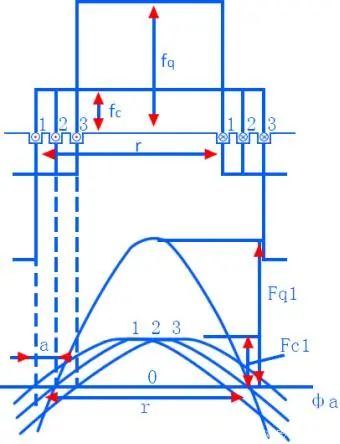
我们一般用一个绕组因数kω1来对基波磁动势进行修正，其幅值为：

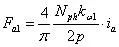
直流电机的相电感与互感计算

根据基波磁动势的幅值，则其沿定子分布为：

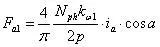
有了磁势，如果能知道磁导（磁阻的倒数），那就能计算气隙磁密了。对于表贴式直流电机而言，气隙基本不变，因此磁导和直流电机转子的位置没有关系；但是对于直流电机而言，气隙沿转子圆周方向一直变换（变化周期是极对数的两倍），因此磁导还和转子位置相关。

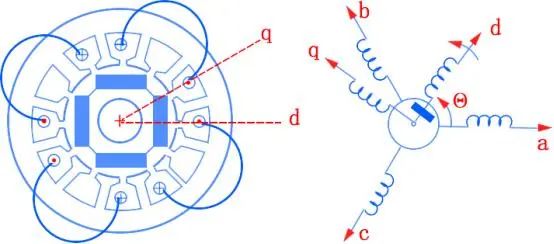
由于dq轴是定义在直流转子上的，因此我们可以通过d轴与A相绕组的夹角θ来表示转子所在的位置。

计算相电感

气隙比磁导为：

λ(a)=λδ0+λδ2cos2(a+θ)

式中因为气隙长度变换周期是极对数的2倍，因此有个2次分量，而且当直流电机类型为内嵌式时， λδ2为负值，即d轴时磁阻最大，磁导最小。

气隙磁动势和比磁导的相位关系为：

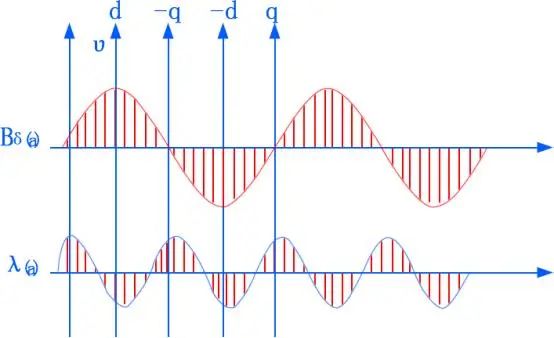
则气隙磁密为磁动势乘以比磁导：

Bδ(a)=Fa1cosa·(λδ0+λδ2cos2(a+θ))

展开成谐波叠加的形式：

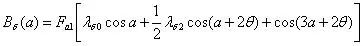
所以基波气隙磁密为：

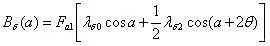
则A相绕组对应的磁链为：

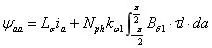
其中 Lσ为A相漏感，τ为极距，l 叠片长度，上式整理可得：

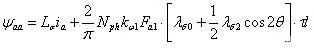
进一步整理可得：

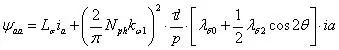
所以A相自感为：

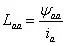
即：

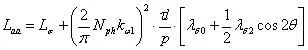
换一种表达方式：

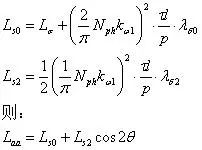
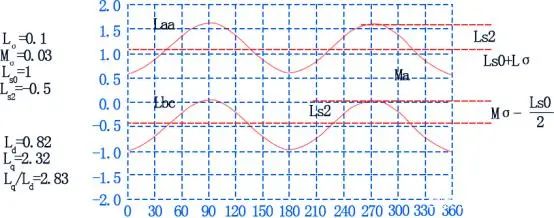
可见，A相绕组的自感不是一个固定值，而是随转子的变换而变化。同理可得其他两相自感为：

Lbb=Ls0+Ls2cos2(θ-2π/3)

Lcc=Ls0+Ls2cos2(θ+2π/3)

计算相间互感

由于B相绕组与A相绕组空间相差120°，其与自感方式基本相同，只需将积分区间由[-π/2 π/2]修改为 [-π/2-2π/3 π/2-2π/3] ，即可以计算A相绕组电流产生的磁场在B相绕组中感应出的磁链，具体为：

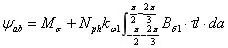
其中Mσ为互漏感，可以获得A、B相互感为：

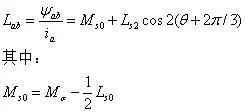
同理可获得其他两相的互感为：

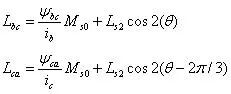
直流电机的自感和互感如下图所示：

如何计算dq轴电感？

一般的直流电机都会用dq轴电感表示，那么问题来了：dq轴电感如何计算或测量？和相电感及互感有什么关系？dq电感和坐标变换有什么关系？

如何确定坐标转换矩阵？

算电感是为了算磁链，进而去计算磁场的某型性质，通过一系列公式，终于把三相绕组的自感和互感计算出来了。

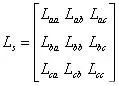
那磁链就可以计算：

电感矩阵非常复杂：

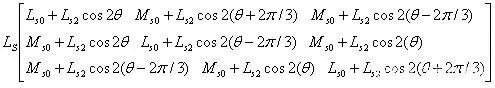
而且这个电感矩阵还随之直流电机转子的变化而变化着，可以找到一个相似矩阵，这个相似矩阵呢形式比较简单，只有对角线上有数，而且这个相似矩阵能表征原矩阵的关键特征。矩阵对角化本质就是寻找矩阵空间的正交基以及在“基”上的投影系数。那电感矩阵是不是可以进行对角化呢？

可以按照矩阵对角化的步骤：

Del|Ls-λI|=0

可以得到三个特征值，分别是：

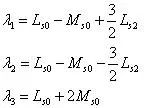
其中特征值λ1对应的特征向量是：

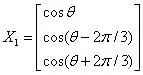
特征值λ2对应的特征向量是：

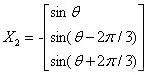
特征值 λ3对应的特征向量是：

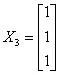
则3个特征向量可以组成如下特征矩阵：

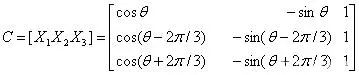
这个特征矩阵就是克拉克变换和帕克变换的乘积，该特征矩阵的逆矩阵为：

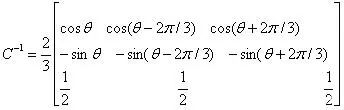
则电感矩阵的特征值可以用特征矩阵及其逆矩阵来计算，即

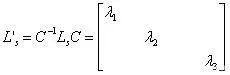
一般称λ1为Ld；

λ2为Lq；λ3为L0，即：

dq轴的电感就是三相绕组电感矩阵的特征值，dq电感是一个常量了，cos2θ等变化因子消失了，也就是说通过对角化（坐标变换），原先较为复杂的电感矩阵对角化和常数化了，是定子的磁链方程解耦了！同时：dq轴电感与变换矩阵无关，是电感矩阵的固有属性。

恒功率变换

在坐标变换的时候，有的变换矩阵前面有个系数2/3 ，有的是

，有的又没有，这到底有什么关系呢？

电压矢量、电流矢量以及磁链矢量的关系为：

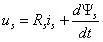
电感对角画的时候求取了变换矩阵C ，现在我们需要把电压矢量、电流矢量以及磁链矢量也进行坐标变换：

Us=Cu’s

is=Ci’s

Ψs=CΨ’s

则变换后的功率为：

P=isTus=(Ci’s)T(Cu’s)=(i’s)T(CTC)u’s

把C 和CT 代入上式，就可以得到：

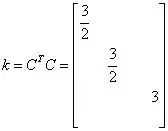
不考虑零轴分量，发现变换后的功率是变换前的3/2倍！也就是说，变换前后功率不守恒了，那通过功率计算的转矩就会不准确了，需要进行修正。

把特征矩阵变为下面这个就可以做到功率守恒

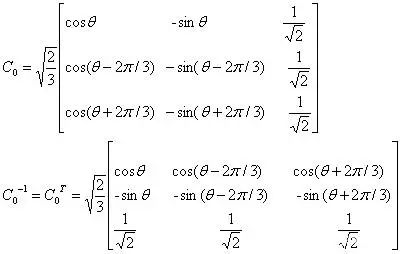
这个矩阵也是最常用的变换矩阵。

dq轴电感测量方法

通过建立直流电机模型，就要知道dq轴电感，两种方式，一种是计算，一种是测量。计算比较容易，建立直流电机的有限元模型，现在的电磁计算软件都有电感矩阵计算功能，计算出来求特征值就行了，有的软件都能直接给出dq轴的电感。

一般来说有2种方式来测电感，一种是通过三相绕组，一种是通过两相绕组。

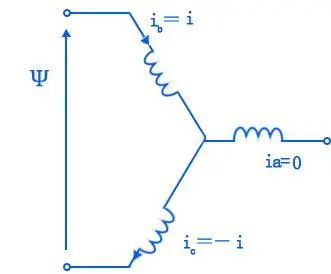
用三相测dq轴电感

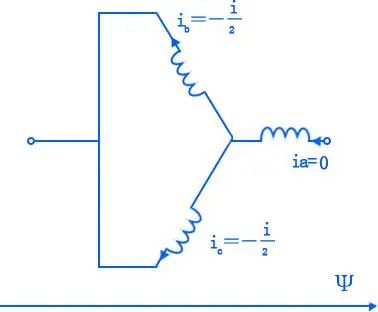
将B、C两相绕组并联在一起，形成一个新的端点，用LCR表或其他装置测量该端点和A相绕组端点之间的电感。

此时因为：

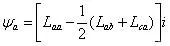
B相绕组和C相绕组并联，具有相同的磁链，因此只计算B相绕组的磁链：

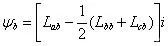
则总的磁链为：

Ψ=Ψa-Ψb

则等效电感为：

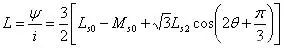
当θ=0时：

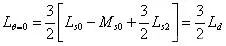
当θ=±π/2时：

可见，当直流电机转子合适的位置测电感时，可以分别获得d轴电感和q轴电感。但是这种方法有一个难点就是如何知道转子此时的位置，一个近似的测法是缓慢的旋转转子，记下电感的最大值和最小值，此时：

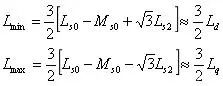
用两相测dq轴电感

用两相绕组也可以直接测量，比如直接测量B、C两相端部之间的电感。

此时，B相绕组的磁链为：

Ψb=(Lbb-Lbc)i

B相绕组的磁链为：

Ψc=(Lbc-Lcc)i

总的磁链为：

Ψ=Ψb-Ψc

等效电感为：

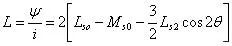
同样，缓慢的旋转直流电机转子，记下电感的最大值和最小值，此时：

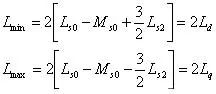
由于直流电机是比较复杂的电磁产品，里面电感构型比较复杂，既有自感又有互感，电感之间既有并联，也有串联，电感串联和并联的特性非常重要

同向串联电感

上图描述了两个绕向相同的电感串联时的模型，其中用黑点表示绕组电流流入方向，电流和磁链方向如图所示。

第一个电感产生的总磁链为：

Ψ1=L1i1+|M|i2

第二个电感中产生的总磁链为：

Ψ2=L2i2+|M|i1

两个电感中的电流方向相同：

i1=i2

两个电感等效成一个电感时，总的磁链为：

Ψ=Ψ1+Ψ2=(L1+L2+2|M|)i

则等效电感为：

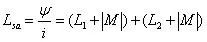
反向串联电感

此时两绕组绕向相反，由于定义的电流正方向为绕组的流入方向，在此规定下，两绕组的电流数值关系是：

i1=-i2

所以总的等效磁链为：

Ψ=Ψ1-Ψ2=(L1+L2-2|M|)i

则等效电感为：

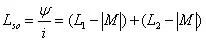
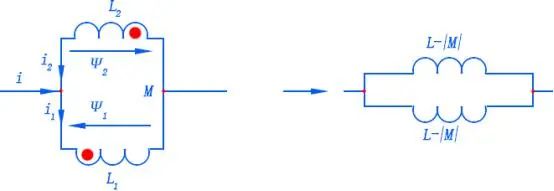
同向并联电感

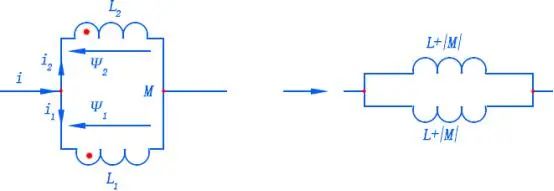
两个电感并联时是比较反直觉的，下面我们就来仔细分析一下。上图是绕向相同的两个电感并联时情况，此时，由基尔霍夫电压定律每个电感两端的电压应该是一致的。即：

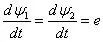
对于第一个电感：

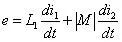
对于第二个电感：

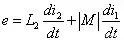
由基尔霍夫电流定律：

i=i1+i2

整理可得：

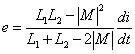
所以等效电感为：

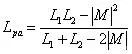
反向并联电感

两电感方向绕向相反，则根据基尔霍夫电压定律：

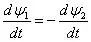
由基尔霍夫电流定律：

i=i1-i2

可计算的等效电感为：

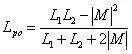
简单来说：

当两电感串联时：Ls-L1+L2±2M ，绕向相同时为+，绕向相反时为-；

当两电感并联时：

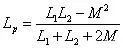
，绕向相同时为+，绕向相反时为 -。