摘要：针对在参数变化、外部干扰条件下四旋翼飞行器的稳定飞行控制问题，本文提出了一种基于反步法的四旋翼飞行器增稳控制方法。首先，建立四旋翼飞行器的动态模型。其次，基于反步法设计的控制器用于飞行器姿态控制，采用模糊自适应PID控制器对飞行器的高度和位置进行控制，将两者结合构成一个内环姿态和外环位置结构的双闭环控制器，从而实现四旋翼飞行器的混合增稳控制。仿真和实际测试结果表明所设计的控制器能够实现参数变化和外部干扰时的稳定控制。

0 引言

　　近年来，由于四旋翼飞行器具有很好的机动性及特殊的机械结构，使其在军事侦察、自然灾害、信息测绘、交通控制、城市应急救援、电影拍摄等领域得到了广泛应用[1-2]。四旋翼飞行器是一种新的微型直升机，通过四个独立的旋翼实现垂直起飞和垂直降落，通过调节四个旋翼的转速来实现其位置和姿态的控制。同其他的机平台相比，四旋翼飞行器有许多优势，例如：悬停能力、体积小、成本低以及强大的环境适应能力。然而，在控制方面，四旋翼飞行器也存在如非线性、多变量、欠驱动性、抗干扰能力弱及易耦合性强等问题[3]。

　　目前，国内外学者针对如何控制四旋翼的位置和姿态问题开展了大量的研究工作。其中，最常见有线性反馈算法[4]、LQR[5]、PID控制[6]以及滑模控制[7]等。这些算法在控制四旋翼飞行器的位姿方面有很好的效果，相应的也有自身的缺点。例如PID和LQR控制算法忽略了模型的非线性因素，而非线性因素对控制结果有不小的影响。另外，PID控制算法不能在线调整参数;线性控制理论LQR不适用于非线性和耦合性强的系统。在文献[8]中，应用了一个集成反步控制器来控制四旋翼飞行器的水平位置和高度。滑模控制算法具有简单、可靠的优点，是一种很有效的控制算法，但是它也带来了颤振现象[9]。文献[10]提出了一种基于解析模型的滑模PD控制器来实现对旋翼的控制。文献[11]针对姿态稳定化问题，采用混合反步算法来创建姿态角加速度函数。整体反步控制算法也可以用于四旋翼的控制，不足的是，整体反步算法需要有精确的模型，且其鲁棒性较差。现有的许多研究均表明，在系统不确定性条件下，滑模控制器有很好的控制效果，但它有很高的增益和控制输入。

　　因此，本文针对在参数变化、外部干扰条件下四旋翼飞行器的稳定飞行控制问题，将反步控制与模糊自适应PID控制相结合，提出一种不仅能达到控制效果，同时具有强大抗干扰能力的混合增稳控制算法。利用不确定参数的更新定律的反步算法和模糊自适应算法来实现飞行器的增稳控制，提高飞行的稳定性。

1 四旋翼飞行器建模

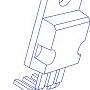
　　四旋翼飞行器的结构原理如图1所示，十字架的末端有四个电机。转子对(1，4)逆时针方向旋转，转子对(2，3)转向与(1，4)相反，来平衡由转子旋转产生的扭矩。转子4速度增加了多少，以相同量级降低转子1的速度，会使机产生倾斜运动，通过调整转子对(1，4)的相对速度来控制机的俯仰角;类似地，通过调节转子对(2，3)的相对速度来控制机的滚转角度;通过调节的逆时针转动的转子对(1，4)和顺时针转动的转子对(2，3)之间的相对速度来控制机的偏航角。推力的控制是通过调节四个转子的速度来实现的。定义系统中两个参考坐标系分别为惯性坐标系和机体坐标系。惯性参考系为Oe(xeyeze)，主体参考系为Ob(xbybzb)。四旋翼机的绝对位置由X=[x，y，z]T和姿态角Q=[φ，θ，ψ]T决定，其中姿态角包含三个方向角度，分别是滚转角(绕x轴)、俯仰角(绕y轴)、偏航角(绕z轴)。由一个在低速环境下的简单四旋翼飞行器动态模型可以得到：

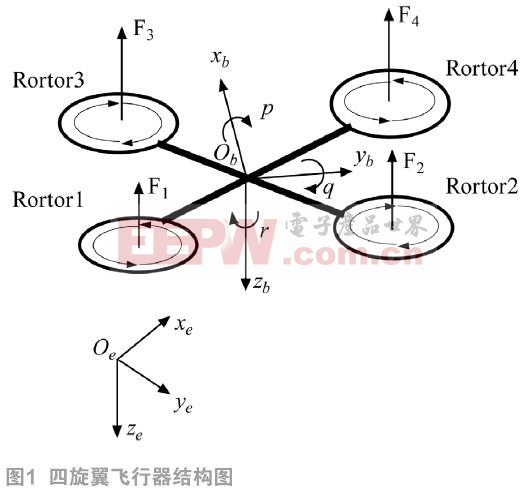
(1)

　　其中，Jr是与空气动力阻力相关的阻力系数，d是四旋翼重心和每个转子中心之间的距离，Ix，Iy，Iz为沿x，y，z方向的惯性矩。定义以下变量：

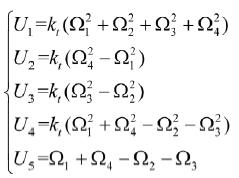(2)

　　通过引入矢量X=[x1，x2，…x12]T作为系统的状态向量，则四旋翼飞行器模型的状态空间形式为：

(3)

2 增稳控制器的设计

　　本文所设计的增稳控制器采用双闭环控制结构，即用于飞行器高度和位置控制的模糊自适应PID控制器构成位置外环，用于飞行器姿态控制的反步控制器构成姿态内环。

　　2.1 模糊自适应PID控制器

　　模糊自适应PID方法是基于应用模糊逻辑概念的智能算法。模糊自适应PID控制器本质上是一种PID控制器，它采用模糊推理系统，根据误差(E)和误差的导数( ΔEC)来调节参数Kp，Ki，Kd。图2给出的是模糊自适应PID控制器的结构框图。

　　模糊规则设计是基于PID控制器的属性。因此，模糊集的输出由输入模糊集和设计的模糊规则得到。在模糊结构的基础上，每个PID控制器有两个模糊推理输入即误差和误差的导数，有三个模糊推理输出，所有的论述都是在这五个模糊子集中共享。模糊规则的语言标签定义如下：NB，负的最大值;NS，负的最小值;ZO，近似为0;PS，正的最小值;PM，正的中间值;PB，正的最大值。模糊输入变量由五个语言变量组成：

　　E= {NB, NS, ZO, PS, PM }。语言变量输出被定义为：ΔKp= {ZO, PS, PM, PB}，ΔKi = {ZO, PS, PM, PB}，ΔKd = {ZO, PS, PM, PB }。模糊推理规则如表1所示。

　　模糊推理规则表是基于输入、输出隶属函数的数量来制定的，所有的输入、输出隶属函数都应该被评估。表一中给出的模糊推理规则可以用下述方法解读：若误差为A，误差的导数为B，输出为C。例如，误差(E)取负的最大值(NB)，误差的导数(ΔEC)取正的最大值(PB)，那么ΔKp输出为正的最大值(PB)。

　　图2给出的是模糊自适应PID控制器的框图，最终的模糊PID参数优化算法是：

(4)

　　对于飞行器高度控制的问题，模糊自适应PID控制器对于高度的控制是线性的，设定跟踪误差为e=zd -z，zd为给定高度，则有，

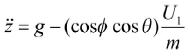(5)

　　其中，g代表重力加速度，当飞行器处于盘旋状态时，假设飞行器滚转角和俯仰角均为0，则公式(5)简化为：

(6)

　　得到高度控制的控制输入为：

(7)

　　对于飞行器的位置控制问题，可以通过控制滚转角和俯仰角大小，使四旋翼机在x，y方向上移动，进而产生运动。控制滚转角大小能够使飞行器沿y轴方向移动，控制俯仰角使得飞行器沿x方向运动。由式(1)可知其动力学模型为：

　　在高度和位置控制环增加了模糊控制模块，在误差E、EC和PID的三个参数之间形成了模糊控制关系。通过监测误差、误差的导数的实时值，对PID算法的ΔKp，ΔKi以及ΔKd进行实时修正。

　　2.2 反步控制器

　　姿态控制不仅影响到飞行稳定性，还是位置控制的必要条件。因此四旋翼飞行器的姿态控制尤为重要。反步控制器的设计是基于以下假设，即系统的滚转角、俯仰角、航偏角满足下列不等式[12]：

　　通过控制输入U1，U2，U3和U4，能够实现四旋翼飞行器的稳定飞行。

3 实验研究

　　3.1 仿真实验

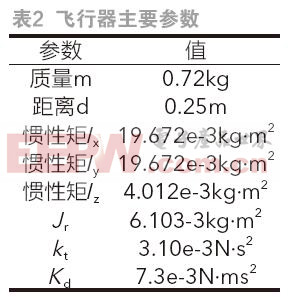
　　在Matlab/simulink中实现了所提出的控制算法，通过抗干扰测试验证本文提出混合增稳控制器的性能。四旋翼飞行器的主要参数如表2所示。

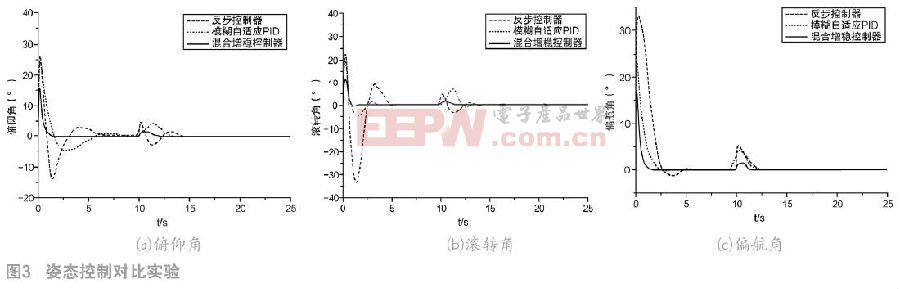
　　为了增强飞行器对在参数不确定性和外界干扰条件下的响应，进行了反步控制器、模糊自适应PID控制器、模糊自适应PID混合增稳控制器的仿真测试。实验条件为在10s时，对每个轴上施加一个扰动，并在13s时移除干扰，姿态控制和高度控制的实验结果分别如图3和图4所示。其中，实线为本文提出增稳控制算法，点划线为反步控制算法，虚线为模糊自适应PID控制算法。

　　由图3和图4可知，本文所提出的混合增稳控制器的调节时间优于反步控制器和模糊自适应PID控制器，超调量最小，稳态阶段的稳态误差类似于反步控制器和模糊自适应PID控制器。在干扰发生期间，所设计的增稳控制器不仅能完成姿态和高度的控制，具有较好的抗干扰能力，而且比反步控制器和模糊自适应PID控制器具有更好的跟踪响应能力。

　　3.2 飞行实验

　　通过实际飞行过程中的抗干扰实验，进一步验证了混合控制器的性能。在t=12s时对四旋翼飞行器的姿态角进行随机干扰，实验结果如图5所示。可以看出，滚转角、俯仰角、偏航角的角响应通常是相似的，均在短时间内收敛到给定值的允许范围内。;在t=7s时对高度控制进行随机干扰，如图6所示。可以看出，高度方向上也有很好的响应，高度值在短时间内达到期望值。在扰动条件下，所提出的增稳控制器能够迅速稳定四旋翼飞行器，具有较强的鲁棒性。当系统稳定时，四旋翼飞行器的姿态角在±3°的控制范围内。

4 结论

　　为提高四旋翼机在参数变化和外部干扰条件下的飞行稳定性，提出并设计了基于模糊自适应PID控制器和反步控制器的混合稳定增强控制方法，实现了对四旋翼飞行器的精确控制。非线性仿真试验结果表明，所提出的控制器可以有效抑制扰动的影响，提高控制精度。通过对自由度四旋翼飞行器的飞行试验，证明了该控制器的稳定性和有效性。