过去，的基础是行为和具有基本结构的模型。这些模型使用的公式我们在学校都学过，它们主要适用于简单集成电路技术中使用的器件。但是，当涉及到时，这些简单的模型通常无法预测与为优化器件所做的改变相关的现象。当今大多数不是横向结构，而是垂直结构，它们使用多个掺杂层来处理大电场。栅极从平面型变为沟槽型，引入了更复杂的结构，如超级结，并极大地改变了MOSFET的行为。基本中提供的简单器件结构没有考虑所有这些非线性因素。

现在，通过引入物理和可扩展建模技术，安森美(onsemi)使精度进一步提升到更高的水平，本文将主要介绍物理和可扩展模型功能的相关内容。

这种基于物理公式、工艺参数和布局参数的建模技术考虑了我们的产品为现代功率开关器件所引入的所有非线性。物理公式可以捕获现代在所有不同区域中的温度依赖性和传播效应。针对专用技术（ MOSFET M3和IGBT FS4等）创建了一个核心模型——通过布局参数设置芯片尺寸，以获取特定的器件。

物理和可扩展仿真模型所包含的值远不止通过数据手册参数或在几乎理想的测量环境中获得的数据手册值。该模型可在规格限值内仿真所有条件下的所有值。在物理和可扩展仿真模型中还可以捕获数据手册中未提供的参数或曲线——可通过仿真获取。大多数时候，只需运行一个简单的仿真原理图。

为举例说明物理和可扩展模型的强大功能，我们将比较通过仿真两个超级结 MOSFET 模型（一个行为模型和一个物理和可扩展模型）获得的输出电容结果。这两个超级结MOSFET性能相近（650V，导通电阻约为18mΩ）。首先，我们将仿真结果与测量数据叠加。

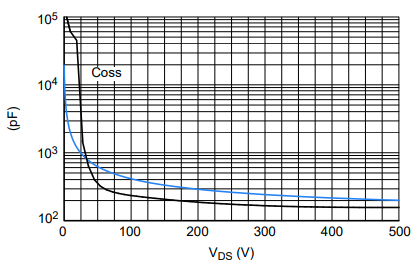
图1. 行为模型输出电容仿真结果

在上图和下图（分别为图1和图2）中，彩色曲线是通过仿真获得的，而叠加的黑色曲线是基于器件规格的曲线。图1来自竞争对手的模型，因为所有安森美超级结MOSFET模型都不是行为模型，而是物理和可扩展模型。行为模型无法捕捉到输出电容近103的下降，这是所有超级结MOSFET固有的特性。

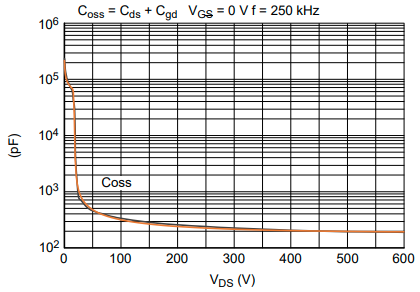
图2. 物理和可扩展模型输出电容仿真结果

接下来，为了比较用于获得图 1 和图 2 的相同硅超级结 MOSFET 模型，我们这次使用相同的对数刻度绘制了输出电容（或COSS）。该刻度放大了差异，但有助于我们读取两种器件在最小阻断电压下的最大电容值和最大阻断电压下的最小电容值的仿真结果，如图 3 所示。

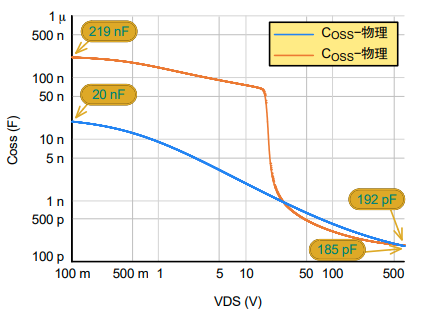
图3. 行为模型与物理和可扩展性模型的输出电容仿真结果比较

假设我们想要使用半桥或全桥结构来仿真软转换或零电压开关应用。在转换期间，我们认为电感电流恒定，这意味着电感足够大。

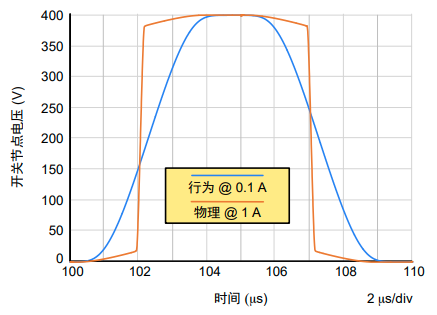
图4. 行为模型与物理和可扩展性模型的输出电容仿真结果比较

我们试图获得几乎相同的转换时间（图4）。由于低电压下电容值具有十倍数差异（参见图3），因此为输出电容充电和获得软转换所需的电流值也有十倍数差异。

如图2所示，安森美物理和可扩展仿真模型给出的输出电容值（或COSS）是准确且真实的。这意味着使用图4中的安森美物理和可扩展仿真模型仿真得到软转换所需的电流也是有效的。

使用行为仿真模型，您会将谐振转换所需的能量低估 10 倍——该误差或错误可能导致需要全部重新设计应用的谐振回路和系统。

现在，您可以使用安森美物理和可扩展仿真模型，以出色的精度仿真零电压开关转换。您将获得转换所需的实际能量，因为仿真模型捕获了COSS在超过103倍变化率范围的所有电容非线性。

物理和可扩展仿真模型功能

使用SIMetrix获取内部节点电压

键合和封装位于芯片和电、热接触点之间。组装通过寄生串联电感和电阻或电阻抗和热阻抗影响芯片性能。封装引脚加上键合和金属掩模可增加高达10mΩ的串联电阻。

为了量化这些影响，可以访问三引脚MOSFET的内部节点，如栅极、漏极和源极（参见图5）。

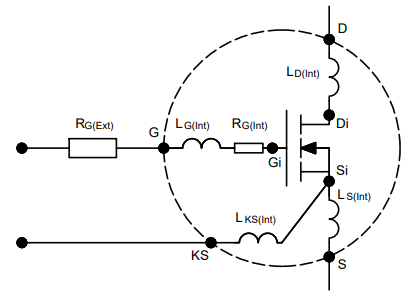
图5. 内部节点与外部节点

在极高速开关中，栅极是硬开关和软开关中最关键的信号。掌握MOSFET何时真正导通和关断非常有必要。例如，它可以帮助设计人员在半桥结构中设置高压侧和低压侧开关之间的延迟。

要访问内部节点，请查找器件和可用引脚名称。引脚标记末尾带有“i”，表示“内部”。

在SIMetrix中，只需在仿真选项控制面板中选择此功能，即可获得内部节点电压。然后，名称看上去类似“Qn:xy:di”（例如）为内部漏极节点电压。它直接是芯片级的电压。我们现在可以测量施加到芯片上的实际漏极-源极电压，不存在任何可能增加或减少振铃的寄生效应。

我们采用由 MOSFET NTHL015N065SC1构成的一个半桥架构，改变外部栅极电阻，并比较芯片级和封装级之间的漏极-源极电压差。该器件采用TO247三引脚封装。

在下图中，我们可以比较导通和关断时的漏极-源极波形。导通时，振铃较低，而关断时则相反（见图6和图7）。

浅色曲线是芯片漏极-芯片源极电压，深色曲线是封装漏极-封装源极引脚电压。

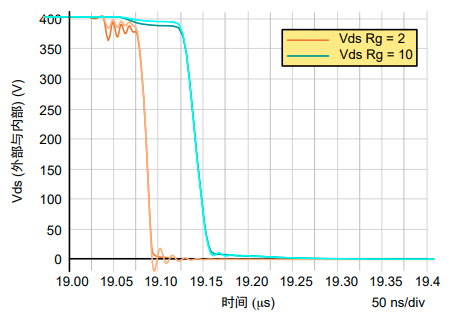
图6. 导通时内部和外部漏极-源极电压的差异

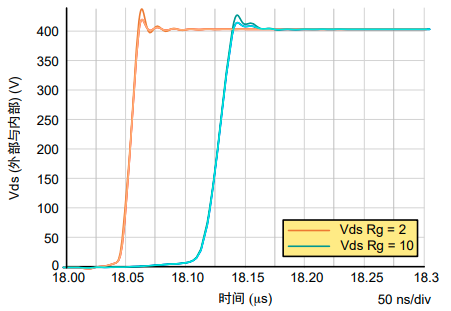
图7. 关断时内部和外部漏极-源极电压的差异

如前所述，获取实际的芯片栅极信号有助于提供相关信息。我们采用一个由 MOSFET NTH4L015N065SC1 构成的半桥架构，改变外部栅极电阻，并比较芯片级和封装级之间的栅极-源极电压差（参见图8和9）。

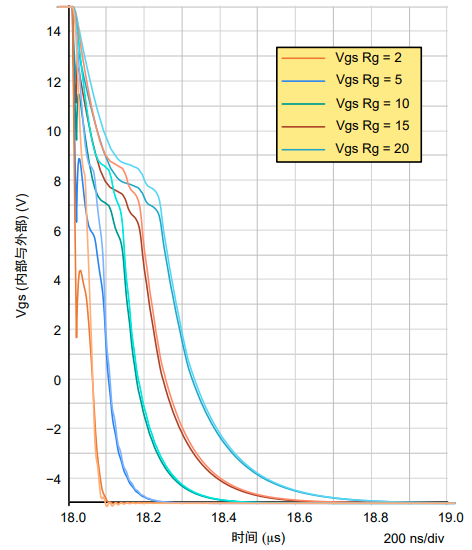
图8. 内部和外部栅极-源极电压的差异及其与外部栅极电阻的函数关系

浅色曲线是芯片栅极电压，而深色曲线是封装栅极引脚电压。

我们来逐步查看当栅极电阻改变时会发生什么。当电阻大于10Ω时，外部和内部栅极电压几乎同时超出阈值（即，对于安森美SiC MOSFET为2V）。存在一个10ns以内的延迟。

当电阻小于等于5Ω时，我们可以看到，在关断期间，只有外部栅极电压会出现电压尖峰和越来越多的振荡，而内部栅极电压相对平滑。

当电阻为5Ω或2Ω时，在阈值交叉处可以明显看到两个电压（外部和内部）之间存在相当大的延迟（约为40ns）。

对于5Ω，外部电压给出的关断时间约为80ns，而内部关断时间约为120ns，因此延长了50%。对于2Ω，情况则更糟。外部电压给出的关断时间约为40ns，而内部关断时间为80ns，因此关断时间延长了100%。

具体取决于外部和内部栅极阻抗之比。在上述图8示例中，内部栅极阻抗略低于1Ω。

在图9中，我们通过改变芯片设计和栅极流道，将内部栅极阻抗提高到接近5Ω，但是对于相同的封装，我们通常会看到一个更长的关断时间，与预期相同。同时，栅极网络的阻尼更大，外部栅极节点电压上的振铃更少。

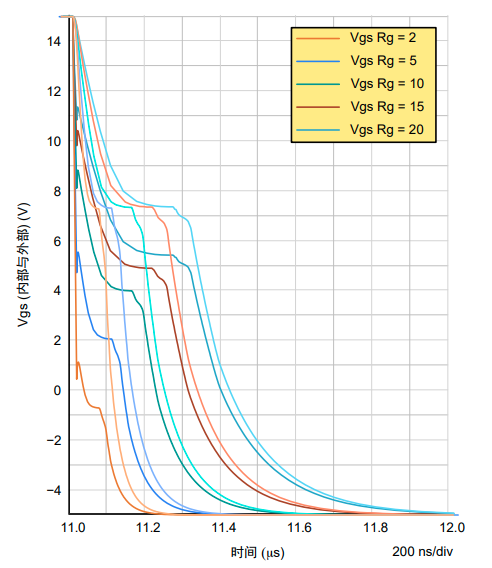
图9. 提高内部栅极阻抗时，内部和外部栅极-源极电压的差异

图9显示当外部栅极电阻低于10Ω时，内部和外部栅极电压之间的延迟较长。一些制造商使用高内部栅极阻抗来降低最大漏极-源极dV/dt和EMI成分，并限制由栅极氧化物应力导致的故障。

然而，依赖外部栅极电压波形来设置半桥或全桥架构中的开关之间的延迟时，也会增加击穿的风险。

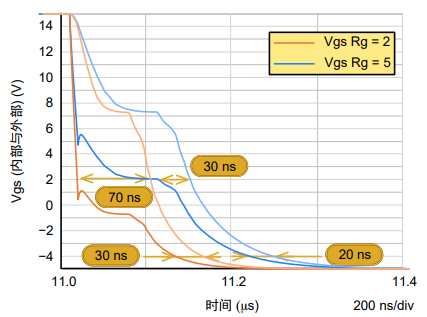
图10. 栅极-源极电压延迟

当外部电阻低于10Ω时，阈值交叉时间存在很大差异，如图10所示。甚至内部栅极和外部栅极信号的过零和关断阈值交叉也会发生在不同的时间。在半桥架构的情况下，MOSFET开关相位不同或采用架构，我们可以测量到外部栅极上得关断延迟要比实际关断时间低得多。因此，会导致另一侧的MOSFET过早打开，并造成严重击穿。

同样，获取内部芯片电压对于设置适当的延迟以避免高压侧和低压侧之间的交叉导通非常有帮助。

使用边界模型

在线提供的模型使用工厂标称值生成和校准。它们给出了典型的数据手册值。

但是，在现实中，由于制造中的工艺差异，参数值遵循高斯分布。

对于特定技术，可以创建具有最小值和最大值的模型。然后，我们可以研究不同器件的并联，或者查看器件随极端情况数值变化的反应。

为了说明该性能，我们采用一个由三个并联工作的 SiC MOSFET 组成的高压降压级电路（参见图 11）。

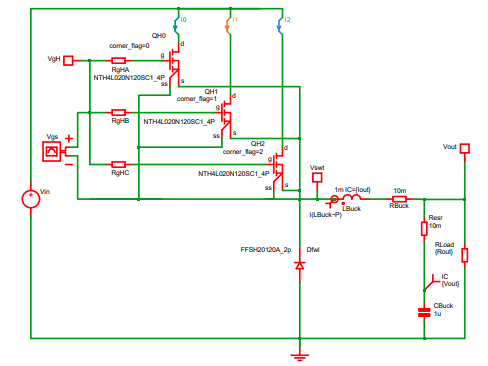
图11. 边界模型降压级

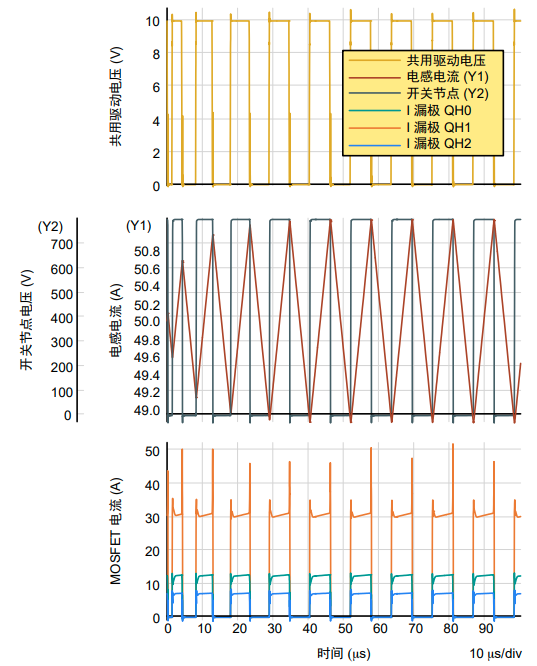
图12. SiC MOSFET 边界模型的降压级波形

图12中的结果显示SiC MOSFET中的电流非常不均衡。在导通时间内，开关或SiC MOSFET中的电流分为30A、12A和7A，电感中的平均稳态电流为50A。流过每个MOSFET的理论电流值约为17A，存在+13/-10A的误差。因此，就电流均衡而言，QH1（最低阈值MOSFET）的误差为+76%，QH0（平均阈值 MOSFET）的误差为-29%，QH2（最高阈值 MOSFET）的误差为-59%。

我们现在还可以使用图13和图14分析导通和关断细节。

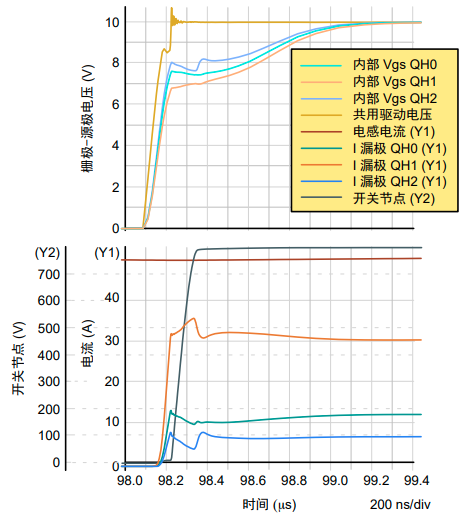
图13. 导通序列局部放大

导通时，如图13所示，在阈值电压最低的SiC MOSFET中流动的电流要高得多。这个MOSFET承受大部分电感电流以及反向容性SiC肖特基二极管电流。此外，并非所有SiC MOSFET的导通损耗都相同。

同样，在关断期间，几乎所有电流都流入阈值电压最低的SiC MOSFET（参见图14）。

我们还可以看到，阈值电压最高的SiC MOSFET的电流首先开始下降，然后阈值电压居中的SiC MOSFET的电流也开始下降。但是，在两个SiC MOSFET完全关断之前，三栅极网络中的谐振会使这两个SiC MOSFET的导通变差，因为它们的整体栅极-源极电压会略有增加。它们在开关节点电压负斜率期间再次导通，但仅占总电流的一小部分。

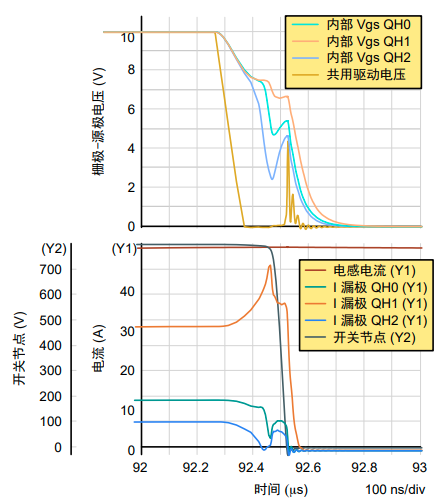
图14. 关断序列放大

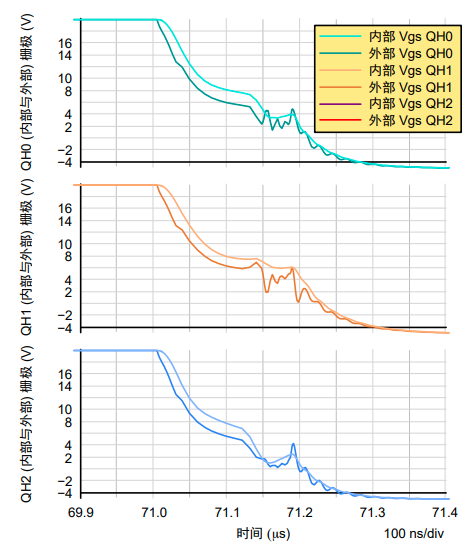
图15. 内部与外部栅极-源极电压关断序列局部放大

同样，如果我们对内部和外部栅极-源极电压之间的差异进行分析，将获得图15中的结果。可以看到在外部栅极-源极电压中存在栅极网络振荡。当开关节点电压为负斜率时，外部栅极-源极电压也会出现明显的尖峰。在图14中，在71.2 μs处的共用驱动电压上也可以看到这个尖峰。

我们可以对漏极-源极电压与漏极电流的乘积进行积分，根据积分周期（导通、关断和导通时间）获得开关损耗能量或导通损耗功率。我们还可以计算同一乘积在一个开关周期内的平均值，以获得每个SiC MOSFET的总损耗。

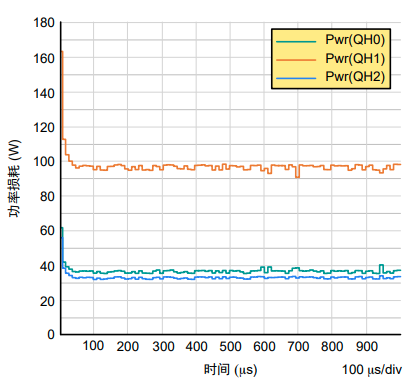
图16. 每个SiC MOSFET的总功率损耗

正如预期和图16所示，阈值电压最低的Si CMOSFET的总损耗最大。

进一步观察可知，最低阈值SiC MOSFET的损耗略低于100W。阈值电压居中的器件损耗介于38W和39W之间，而最高阈值SiC MOSFET损耗则为36W至37W。

当我们使用迟滞控制或自振荡反馈时，开关频率不是很稳定。这会导致每个周期的一些仿真和计算误差。仿真精度和随机变化的仿真时间步长也会引起误差——转化为曲线上的某些噪声。

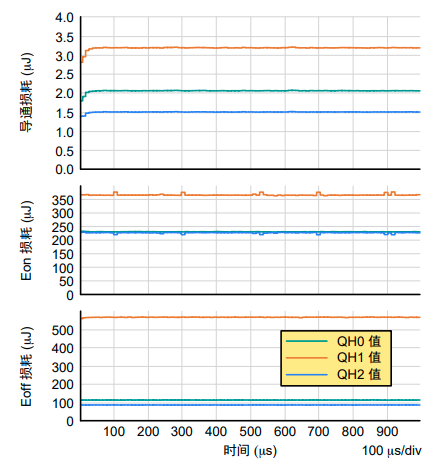
图17. 每个SiC MOSFET的导通、关断和导通损耗能量

每个开关周期内的导通损耗（参见图17）与每个SiC MOSFET中的导通电流保持一致。这并不令人意外。

对于导通能量，最低阈值SiC MOSFET的平均导通能量为400μJ，与其他两个的250μJ相比，几乎翻倍。

在阈值电压最低的SiC MOSFET中，关断能量要高出很多，超过550μJ。阈值电压居中的SiC MOSFET具有120μJ的关断能量，而阈值电压最高的SiC MOSFET的关断能量仅为90μJ。其中一个MOSFET与其他MOSFET的差异达到五倍。