*基金项目：西安石油大学研究生创新与实践能力培养计划项目资助（YCS2211 3156）

载人离心机是航空航天医学专用的大型地面实验设备，也是航空航天医学领域唯一能够实现各种机动飞行动作的地面仿真模拟装置，能够使测试者真实感受飞行对人体生理和心理造成的影响，辅助检查、评估和鉴定飞行人员身体耐力是否与其匹配，飞行人员可以通过离心机训练提高抗荷耐力^[1]。随着航空技术发展，载人离心机更加倾向于进行三轴G 值模拟训练，能在地面上以更加安全和成本较低的方式通过模拟训练来提高飞行员在高过载环境中飞行操纵能力和战场生存率。无刷直流电动机(brushless direct current motor, BLDCM) 具有效率高、可靠性高、启动转矩大、降低电气噪声等优点，在各行各业得到了广泛的应用^[2]，各种技术应用也层出不穷，如，无刷直流电机的模糊控制器，采用粒子群优化算法对其参数进行优化^[3]；研究基于模糊系统的无刷直流电机矢量控制^[4]；提出基于自适应网络的模糊控制器，以提高无刷直流电机的性能^[5]；提出一种基于遗传算法优化的模糊控制器，并与模型参考自适应控制器相比研究其有效性^[6]；比较神经模糊控制器、模糊PID（proportional integral derivative）控制器和常规PID 控制器对无刷直流电机速度控制的性能^[7]。上述技术的主要局限性和缺点是基于进化的优化算法复杂度高、计算量大，不适合工业应用。

本文根据载人离心机设计了短臂复合运动离心机主轴电机控制系统，为设计出适用于短臂复合运动离心机控制系统，要求控制离心机主轴转动的电机调速高效且平稳。因此，选用无刷直流电机作为离心机主轴电机，构建了带负载主轴旋转系统仿真模型，通过该模型得出了带负载时电机的转速、反电动势、电磁转矩、相电流，仿真结果比较理想，验证了该模型的准确性和可靠性。

1 离心机结构及运动分析

短臂复合运动离心机的机械结构如图1 所示，由主轴系统、支撑系统、传动系统、转臂系统和复合运动载人系统组成。主轴系统包括无刷直流电机及回转轴承，其主要功能是实现短臂复合运动离心机以中轴线为中心做360°回转运动；支撑系统主要是支撑方轴，其主要功能是支撑短臂复合运动离心机的机械结构；传动系统主要由减速器组成；其主要功能是传递输出扭矩和转速；转臂系统包括两只转臂，这样可以提高实验的效率，同时也可以构成对称形式，形成对比训练，极大提高了数据的采集效率；复合运动运动载人系统主要由座舱、摆动步进电机、位移步进电机，舱内座椅在离心机轴线方向可实现正负75° 旋转姿态和前后位置动态可调节，可调节座椅靠背角度和前后位置可手动调节。

短臂复合运动离心机在运行时，无刷直流电机通过外部连接减速机带动回转轴承，从而使整个短臂复合运动离心机做回转运动，座舱分别通过两个步进电机来实现前后位置位移及正负75° 摆动。

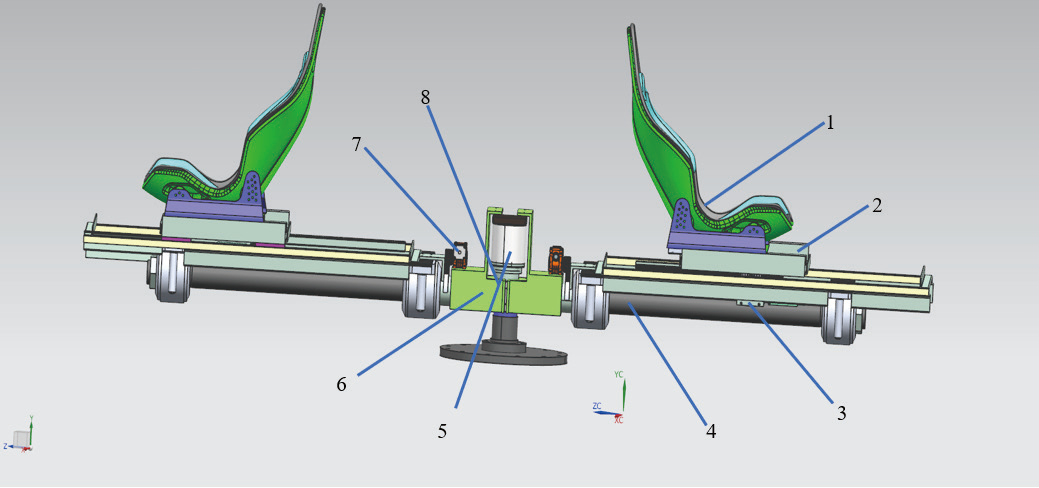
1.座舱；2.座舱移动导轨；3.位移步进电机；4.转臂；5.无刷直流电机；6.支撑方轴；7、9.摆动步进电机；8.减速器

图1 短臂复合运动离心机机械结构示意图

2 主轴电机的等效模型

2.1 电压平衡方程

建立BLDCM 的数学模型，进行以下几个条件的假设^[8]：

1）假设无刷直流电机内部的电感、电阻和互感都相同；

2）忽略电机磁路饱和，齿槽效应和电枢反应等因素；

3）不考虑无刷直流电机绕组电枢反应，电机三相绕组对称且均匀连续分布；

4）忽略了磁滞、集肤和涡流效应和运行时温度变化等因素对电机参数产生的影响。

由以上假设条件，可得几个表达式成立如下：

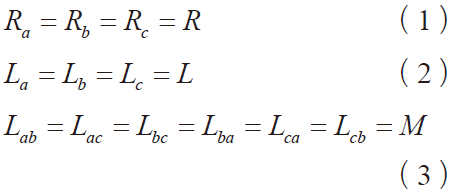
其中，R_a 、R_b和R_c为定子每相电阻( Ω )；L_a、L_b和L_c为定子每相绕组电感(H)； L_ab、L_ac、L_bc、L_ba、L_ca、L_cb为定子每相绕组间互感(H)。

则可以推导出出无刷直流电机的电压平衡方程为：

式中： U_a、U_b、U_c为电机的三相定子绕组电压(V)；i_a、i_b、i_c为定子每相绕组相电流(A)； E_a、E_b、E_c为电机每相绕组相反电动势(V)。

BLDCM 内部等效原理图如图2 所示。

图2 BLDCM等效电路图

BLDCM 内部三相电流的关系表达式为：

2.2 电磁转矩方程

假设将每个绕组产生的电能转化 为机械功率，则电机的电磁功率是三相绕组的电磁功率之和，则有^[9]：

则转矩方程的表达式为

式中，Te为电磁转矩( N⋅m )；ω 为转子角速度(rad/s)。

2.3 机械运动方程

直流无刷电机的运动方程表达式为^[10]

式中，T_L为负载转矩( N⋅m )；B为阻尼系数( N⋅m⋅s / rad )；ω为转子角速度( rad / s )， J 为转子的转动惯量( kg ⋅m²)。

3   主轴电机仿真模型的设计

在构建硬件系统前， 首先需要基于MATLAB/simulink 环境下搭建控制系统的仿真模型，通过仿真的结果来评估该想法的有效性。在无刷直流电机（BLDCM）的实际使用过程中，使用频率最高的是闭环控制方式，这主要是因为开环控制系统运行较不平稳，另外它的控制效果并不是很好。无刷直流电机应用双闭环控制，可使控制系统调控过程简便，扩大控制系统调速范围，并能维持良好控制响应。

BLDCM 仿真模型的总体控制系统结构框图如图3 所示。总体为双闭环控制，外环为速度环，由PI 调节器构成，内环是电流环，采用电流滞环的方式。速度控制器的输入为参考转速，电流环接受三相电流输出作为电流给定值，其与电流检测反馈的实际信号对比得到电流误差，电流调节器的输出控制PWM 波，进而实现无刷直流电机的转速调节。

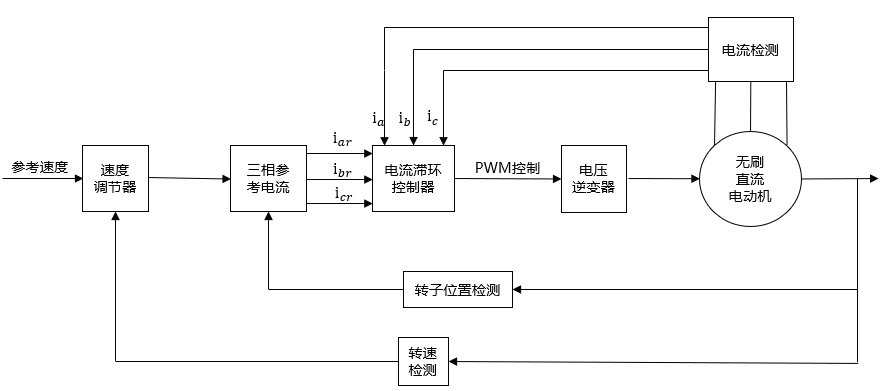
图3 BLDCM闭环控制系统整体框图

3.1 速度控制模块设计

如图4 所示为速度控制模块，参考速度和实际反馈速度共同输入速度PI 调节器，速度PI 调节器的结构如下图所示。具体的参数可以参见模型。在PI 控制器不加抗积分饱和的情况下，当扭矩大范围内波动，则会出现很严重的积分饱和问题，电机转速长时间存在稳态误差。增加抗积分饱和后，得到很大改善。速度PI调节器输出值进入电流计算模块( K_p为比例系数， K_i为积分系数)。

图4 速度PI控制调节器

3.2 参考电流模块设计

参考电流模块的作用是根据PI 调节器输出值I_ref和位置信号Pos 进而给出的三相参考电流，输出的三相参考电流Ia_ref、Ib_ref、Ic_ref 作为电流滞环控制模块的输入，这里的Iref 使用了S函数来实现三项参考电流和转子位置之间的关系，最后通过与实际电流比较进行控制。如图5为参考电流模块。

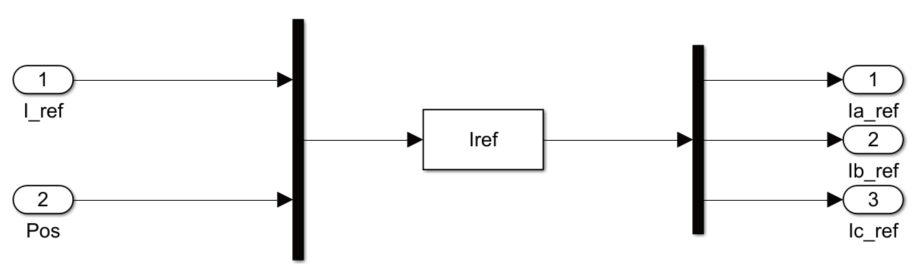
图5 参考电流模块

3.3 电流控制模块设计

电流控制模块采用电流滞环控制原理，目的是让实际电流不断和参考电流对比。当参考电流与实际电流的偏差超过一定值时，调整逆变器，使逆变器输出的电流改变，控制偏差在一定范围内，电流滞环模块如图6 所示。

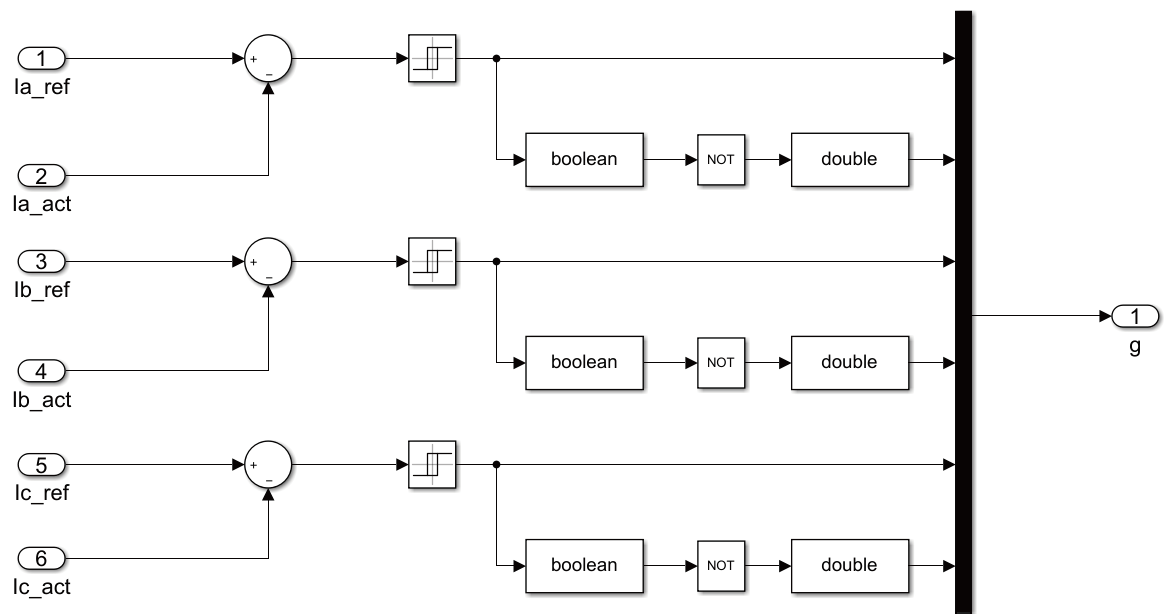
图6 电流滞环模块

3.4 电压逆变器模块设计

在无刷直流电机仿真模型中，逆变器模块具有调节PWM 的作用。如图7 所示，该模块采用了分立式的驱动桥臂。根据电流滞环模块发出的PWM信号，按照一定的频率顺序执行导通和关断，同时输出相对应的三相端电压信号。

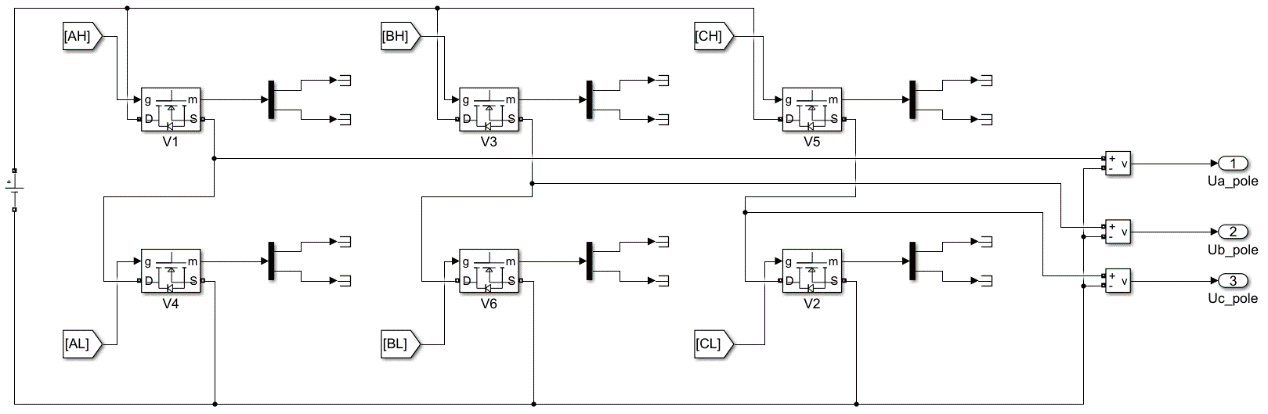
图7 电压逆变器模块

3.5 主轴电机本体模块设计

纵观仿真模型，电机本体模块对速度控制系统来说最为关键，其用来获得电动机的各类参数，例如电机转速，相电流，反电动势，电磁转矩等。要取得效果优良的反电动势是控制中的关键。根据电压平衡方程（4）以及反电动势和转子位置之间的关系， 使用S函数用来实现分线性法来获得三相电流和反电动势；并根据电磁转矩方程（7）计算转矩；通过加法器和乘法器求出T_e ，并根据机械运动方程(8)，经过加乘、积分环节求出转速n 。如图8，由于电机本体模块过大，展示主轴电机本体模块输出部分。理想的反电动势波形图如图9 所示。

图9 中，横坐标为电角度ωt，纵坐标是反电动势E_a、E_b、E_c，三相反向电动势波形一致，仅相位互差为120° 。由角速度和转子位置可得到各个相反电动势变化轨迹直线方程。

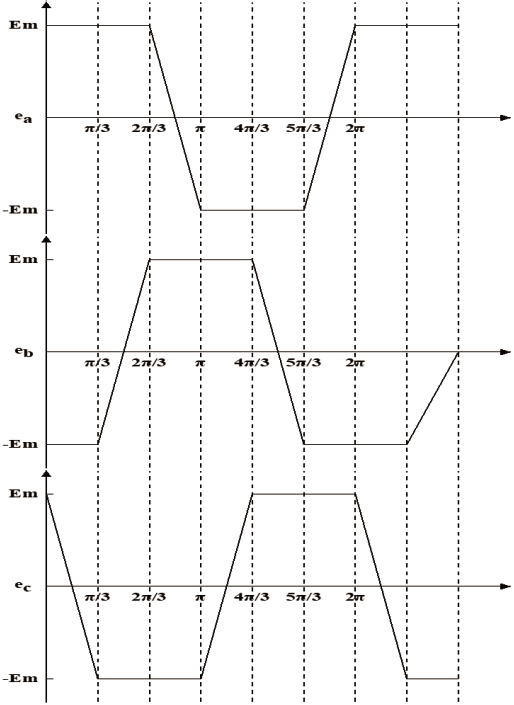
图9 三相反电动势波形图

4   仿真结果及分析

根据无刷直流电机的运行特性以及数学模型，设计出了离心机控制系统的仿真模。如图10 所示，建立无刷直流电机的仿真总体模型图。BLDCM仿真参数设置为：供电为 60V直流电源，B=2 m，J = 0.5 g ⋅m²；R=4.765Ω，L=2.5mH，M=-61mH，负载转矩为2N⋅m，n=2000r / min 。PI 调节器参数为K_p=2.3 ， K_i=0.5 ，采样周期T=1μs 。

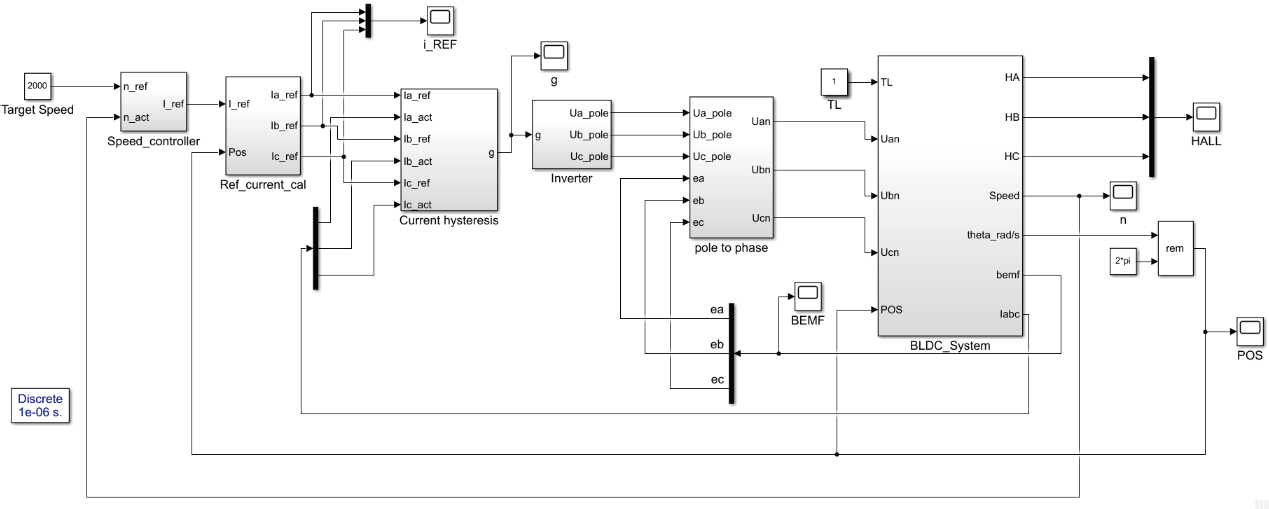
图10 BLDCM仿真总体模型图

仿真系统转速、转矩、三相反电动势和三相电流波形如图11 ～ 14 所示。

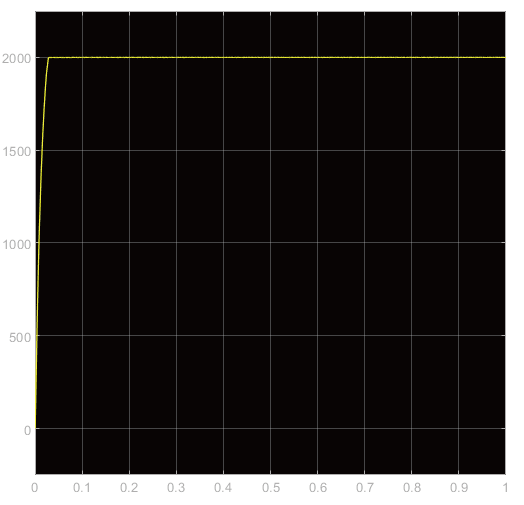
图11 转速波形图

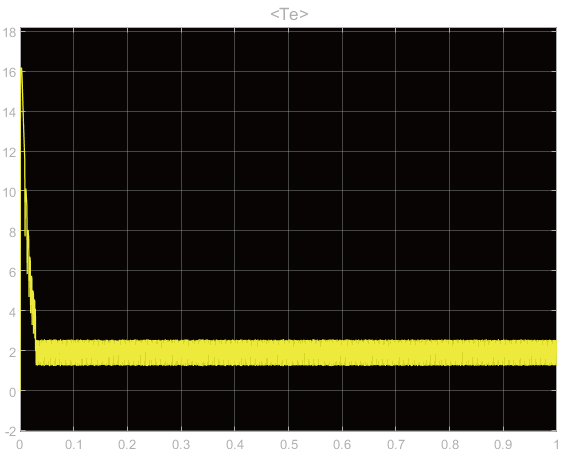
图12 转矩波形图

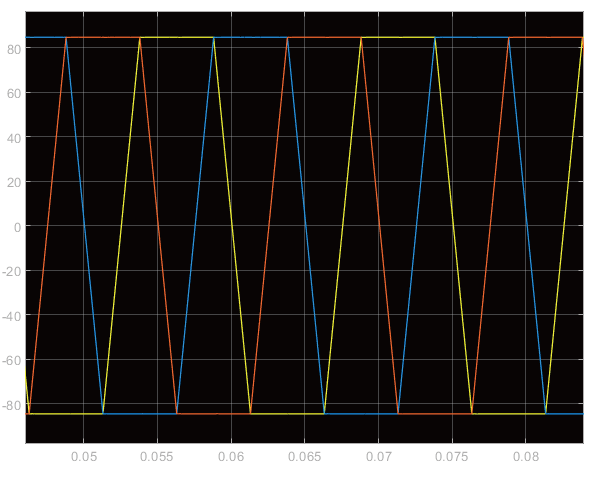
图13 反电动势波形图

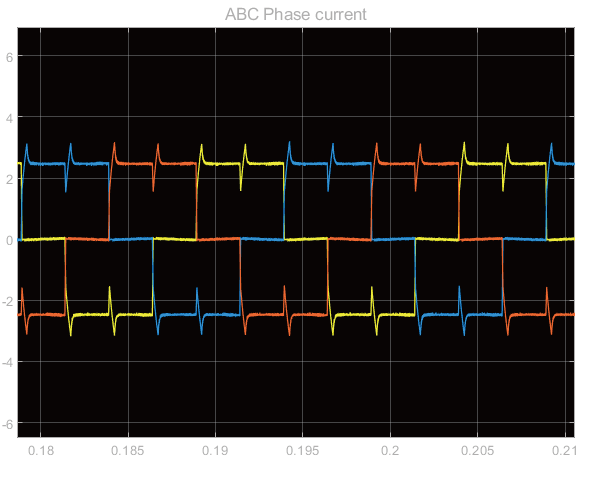
图14 三相电流波形图

从仿真后的波形图可以看到，当无刷直流电机在带负载转矩为2N⋅m时，在 0.02 s 达到了 2000 r/min的转速，系统响应讯速且非常平稳，而且没有超调量现象，转矩波形图也非常稳定，反电动势和三相电流波形较为理想，可为后续应用。

5   结束语

本文根据短臂复合运动离心机主轴控制要求，设计了作为主轴电机的系统。首先，对无刷直流电机进行了结构及运动分析，然后通过推导电机的电压平衡方程，电磁转矩方程和机械运动方程建立了无刷直流电机的数学模型，设计了无刷直流电机的整体控制框图，整体采用双闭环控制方式，外环转速环采用PI 调节器，内环电流环采用电流滞环的方式，基于MATLAB/simulink 环境下依次建立各个仿真模块，最后进行仿真，结果表明：转速响应迅速且平稳，转矩、反电动势和三相电流波形图效果理想，验证了所建模型的精度，为后续整个控制系统的运行提供了理论依据。

参考文献：

[1] 李毅峰, 蒋科, 李宝辉,等.高性能载人离心机的基本结构,原理和故障维修[J].医疗卫生装备, 2021(7):19-22.

[2] KIM C H, LEE K D. Enhanced PID control method for electromagnetic suspension via convex combination methods[J]. Learning, 2016(2):177-182.

[3] WANG G, HUANG Z, DAI M. Fuzzy control research for brushless DC motor based on improved particle swarm algorithm[J]. Guangxi Normal Univ (Nat Sci Ed), 2016, 2(5):36-39.

[4] SHENG Y, WANG X, WANG L, et al. Fuzzy-PID control system design of brushless DC motor based on vector control[C].2017 Chinese automation congress (CAC). IEEE,2017: 5583-5587.

[5] WANG M S, CHEN S C, SHIH C H. Speed control of brushless DC motor by adaptive network-based fuzzy inference[J]. Microsystem Technologies, 2018, 24(1): 33-39.

[6] DASARI M, REDDY A S, KUMAR M V. GA-ANFIS PID compensated model reference adaptive control for BLDC motor[J]. International Journal of Power Electronics and Drive Systems, 2019, 10(1): 265.

[7] HASSAN A K, SARAYA M S, ELKSASY M S, et al. Brushless DC motor speed control using PID controller, fuzzy controller, and neuro fuzzy controller[J]. Learning, 2018(1):112-115.

[8] 胡满红, 李虹飞. 基于单片机和模糊 PID 的拖拉机空调电机控制系统[J]. 农机化研究, 2022(8):76-79.

[9] KNYPINSKI Ł, KUROCZYCKI S, MARQUEZ F P G. Minimization of torque ripple in the brushless DC motor using constrained cuckoo search algorithm[J]. Electronics,2021, 10(18): 2299.

[10] 吴建波, 朱凌云, 陈光琛, 等. 基于无刷直流电机的皮带传送系统设计及仿真[J]. 计算机与数字工程, 2020, 48(8): 2038-2045.

（本文来源于《电子产品世界》杂志2022年12月期）