一、扇区矢量切换点确定

模型按七段式的三相桥臂切换时间搭建，如I扇区内，确定逆变臂的开关顺序为七段000-100-110-111-111-110-100-000；

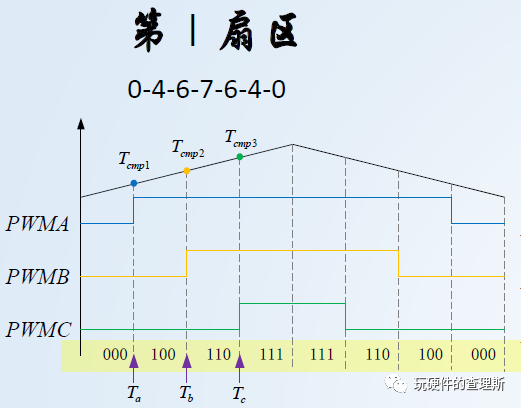
（第I扇区）

由于其为三角波调制，其定时中心对称、每个合成矢量的作用周期固定为Tpwm，则可定义：

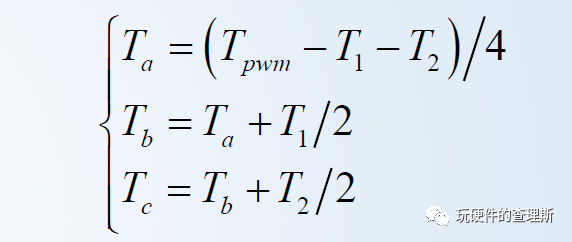
（三相切换点）

同理在第Ⅱ扇区内，逆变桥臂的开关顺序为000-010-110-111-111-110-010-000：

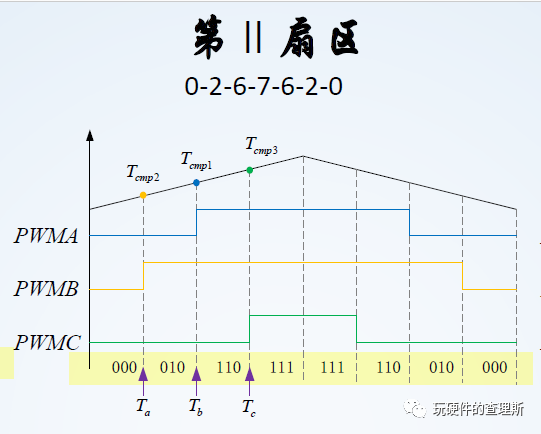
（第2扇区）

在第Ⅲ扇区内，逆变桥臂的开关顺序为000-010-011-111-111-011-010-000：

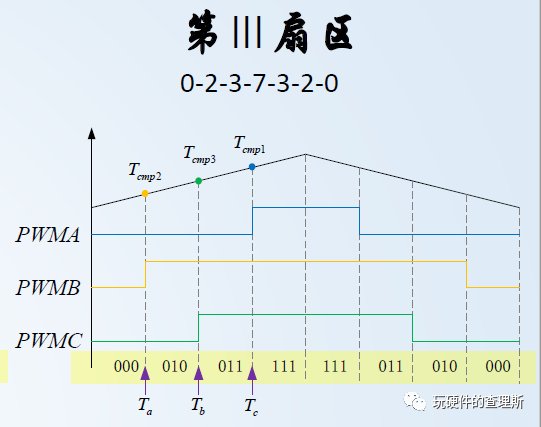
（第3扇区）

在第Ⅳ扇区内，逆变桥臂的开关顺序为000-001-011-111-111-011-001-000：

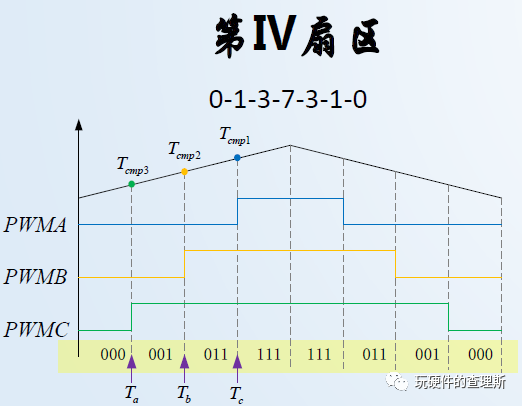
（第4扇区）

在Ⅴ扇区内，逆变桥臂的开关顺序为000-001-101-111-111-101-001-000：

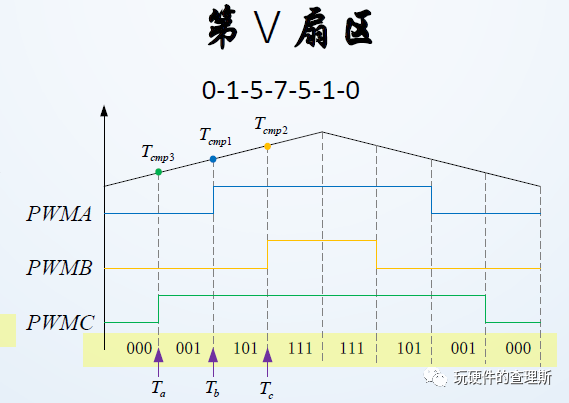
（第5扇区）

在Ⅵ扇区内，逆变桥臂的开关顺序为000-100-101-111-111-101-100-000：

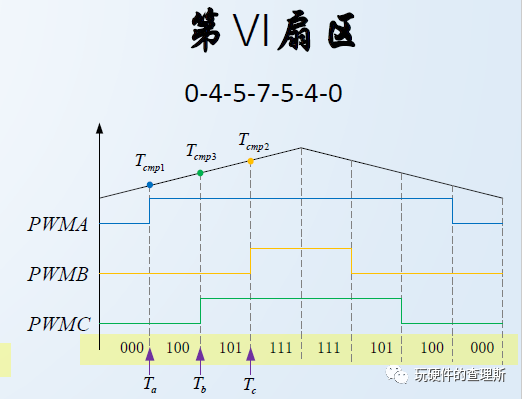
（第6扇区）

三相电压开关比较切换点Tcmp1、Tcmp2、Tcmp3与各扇区的关系可列出如下表格方便查询：

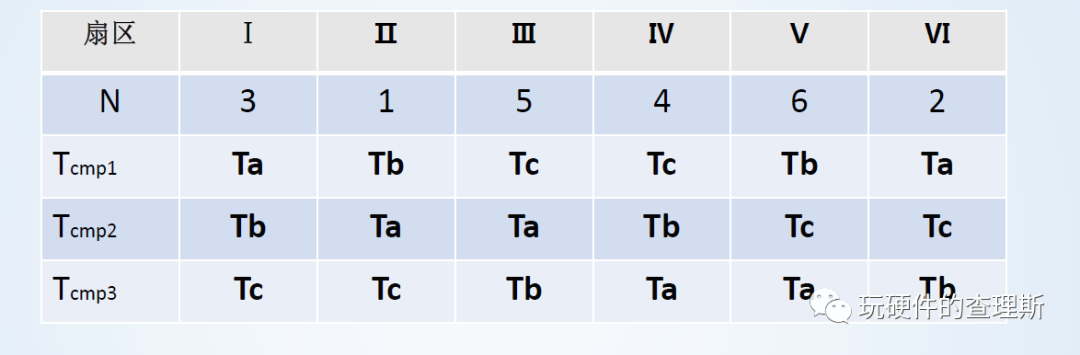
（扇区切换表）

综上我们得到了各时刻所需的空间电压矢量及持续时间，实际应用中可在处理器中赋值对应通道的定时器，捕获比较寄存器产生PWM波形，控制逆变桥，进而产生期望的电压、电流、力矩。

二、基于simulink仿真建模

基于以上的分析，为了验证该算法是准确性，接下来我们就根据原理搭建相关模型：

搭建切换点定义模块如下，输入变量为过调制后的T1、T2及Tpwm；

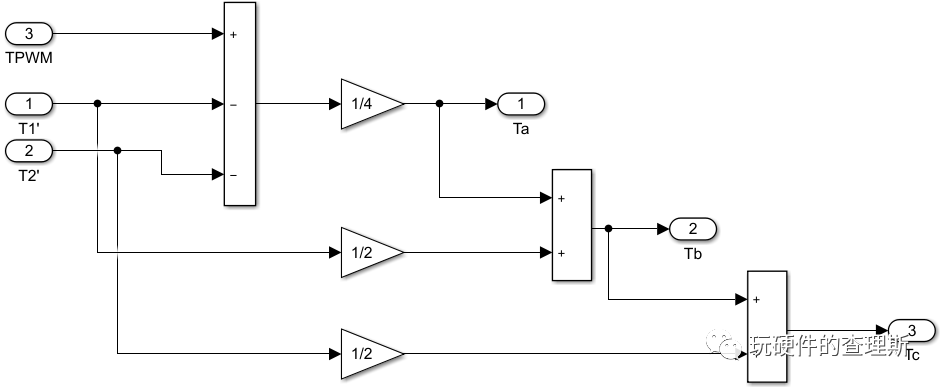
（切换点定义）

搭建根据扇区自动选择相应的比较切换点模块如下，输入变量为扇区N及三相切换点Ta、Tb、Tc，此处我们需要留意，各扇区内三相切换点相对于的载波比较点并不一致，这与马鞍波密切相关；

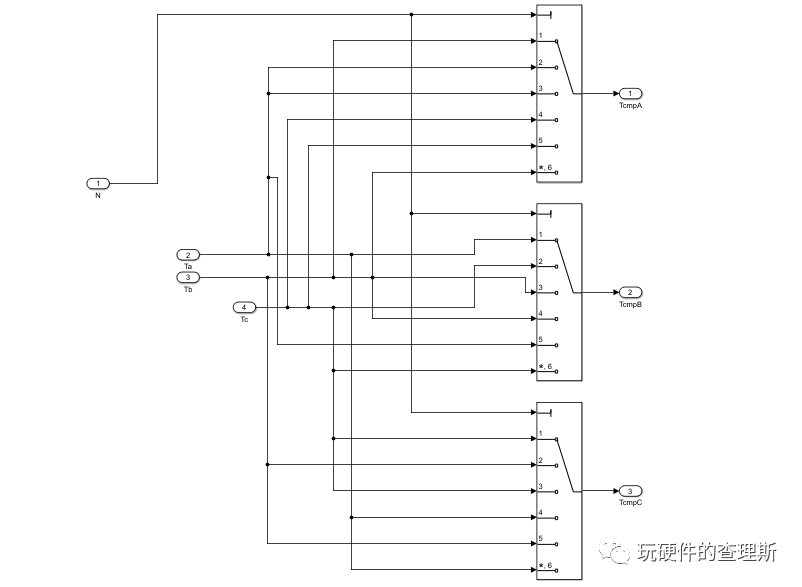
（各扇区自动选择切换点模块）

搭建PWM互补输出模块，输入变量为三角载波与比较点，差值比较输出开关动作，由于此模型仅验证其原理，所以并没有依据实际应用加入死区时间；

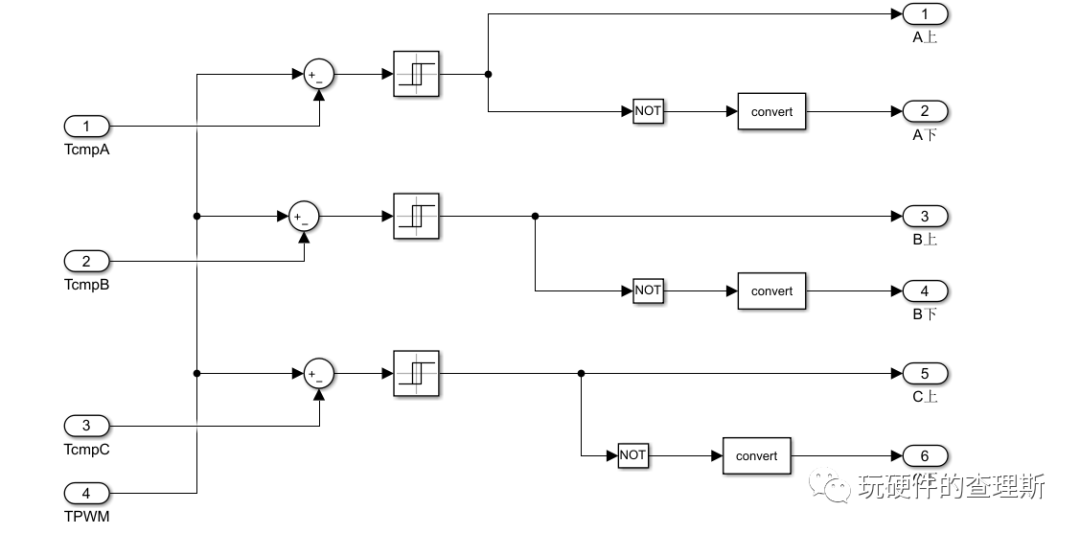
（互补PWM输出模块）

（Spwm汇总模块）

综上就是SVPWM算法的实现方式，其中主要包括参考电压矢量的扇区判断、零/非零矢量用时间计算以及切换时间点确定，最后利用三角载波与切换点比较输出PWM。到这我们将SVPWM模块汇总到单个模块方便后续调用，后接的逆变桥与电机就直接使用simulink库自带的模型。

三、开环仿真运行验证

到这我们搭建开环SVPWM模型验证各项参数，将之前已经搭建的功能模块连接起来，逆变桥与电机选用simulink库自带模块。具体参数设置为：直流侧电压Udc =96 V，PWM开关频率16KHz，仿真算法采用变步长ode23 tb 算法，仿真步长设置为5e^-6，其余变量保持初始值不变。

仿真条件为：给定Ud、Uq值进行Park反变换为三相正弦，Clark正变换为α、β给到Svpwm模块。电机给定转速设定为600 r/ min ，初始时刻负载转矩0.1N•m 。

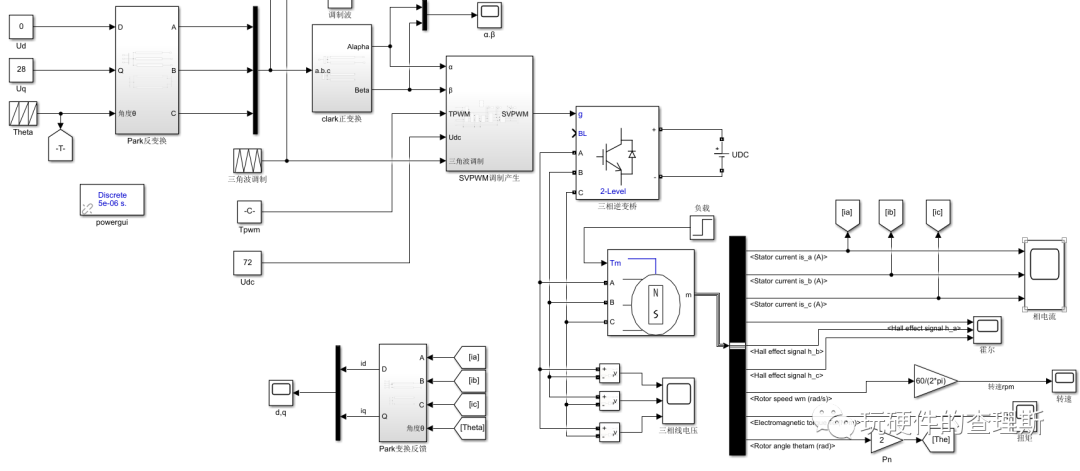
（开环总体框架）

（逆变桥模块）

（电机模块）

设定Ud为0，Uq=24V，仿真运行首先我们看切换点前后的马鞍波，从仿真波形来看到其实马鞍波的来源是三相切换点时间的组合值，当然网上很多资料推测是三相正弦叠加而来这个说法是有待商榷的。

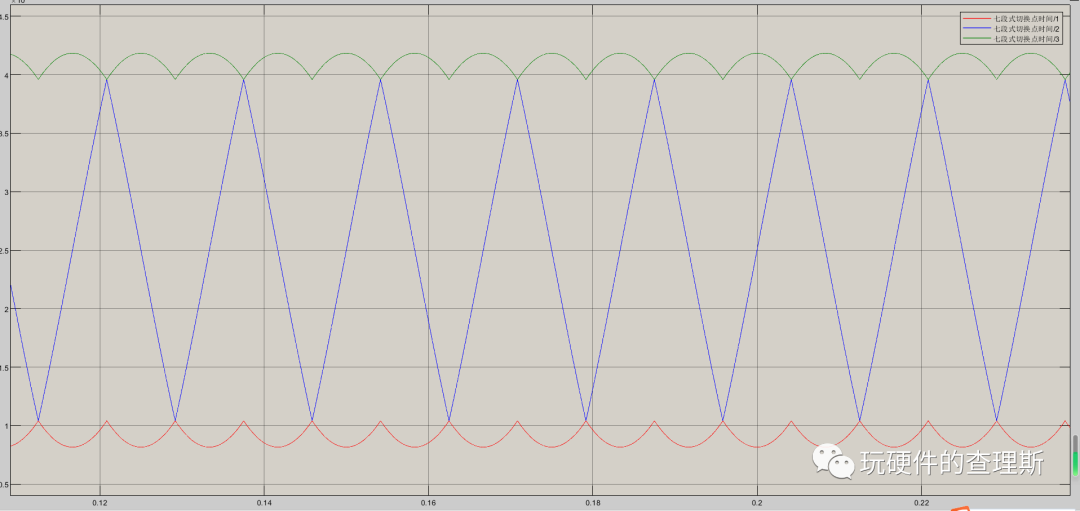
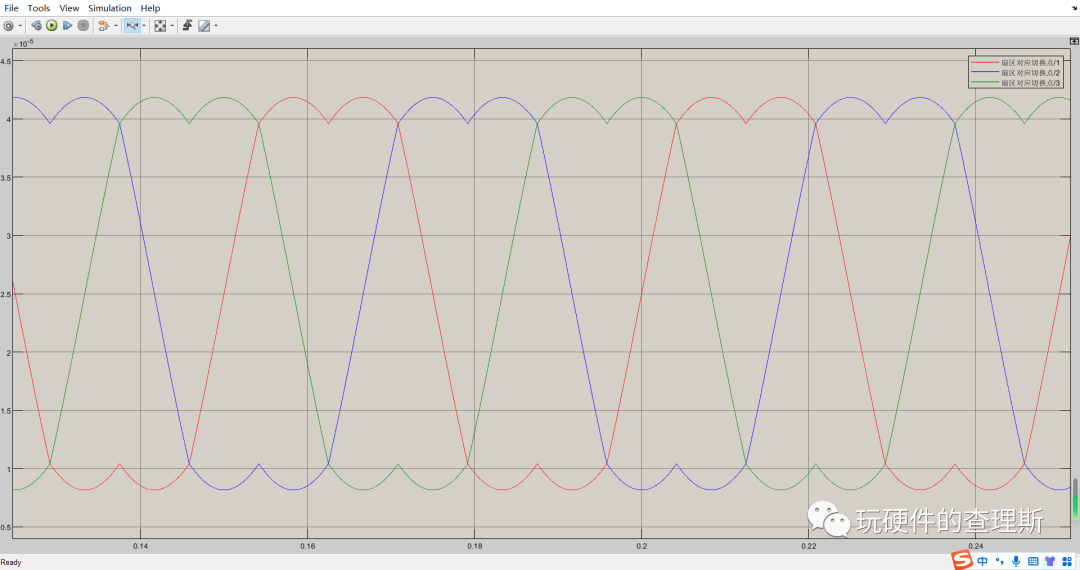
（切换点前后马鞍波）

根据仿真我们可以得出结论：其实马鞍波是SVPWM算法的特点，计算得到的三相切换点时间波形就是如此，只是经过了不同扇区的组合，才形成了马鞍波,并不存在三次谐波。

如下为电机转速波形，开环的效果比较理想，虽然启动时有较大的超调量，但是转速很快就能稳定在600转，但由于没有引入闭环控制，所以还是有轻微的波动。

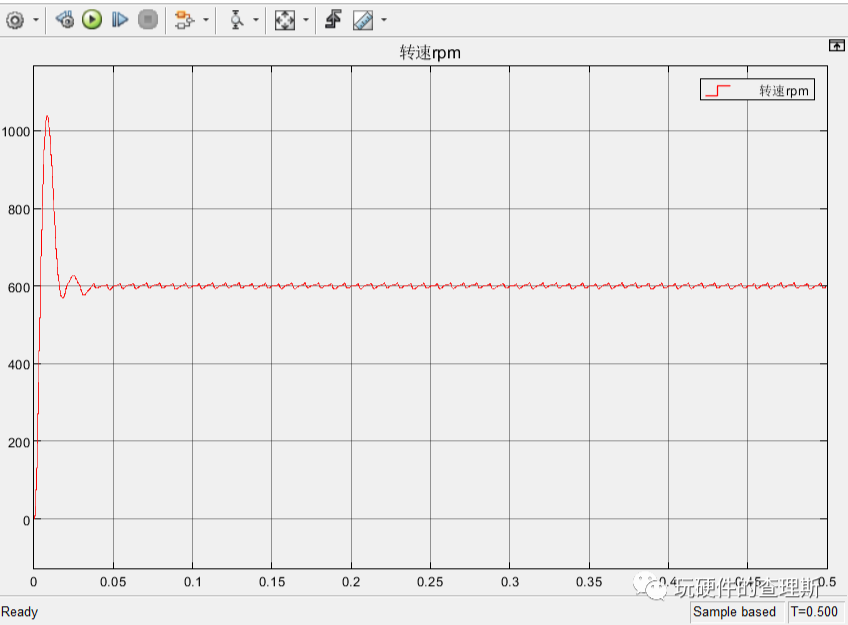
（转速）

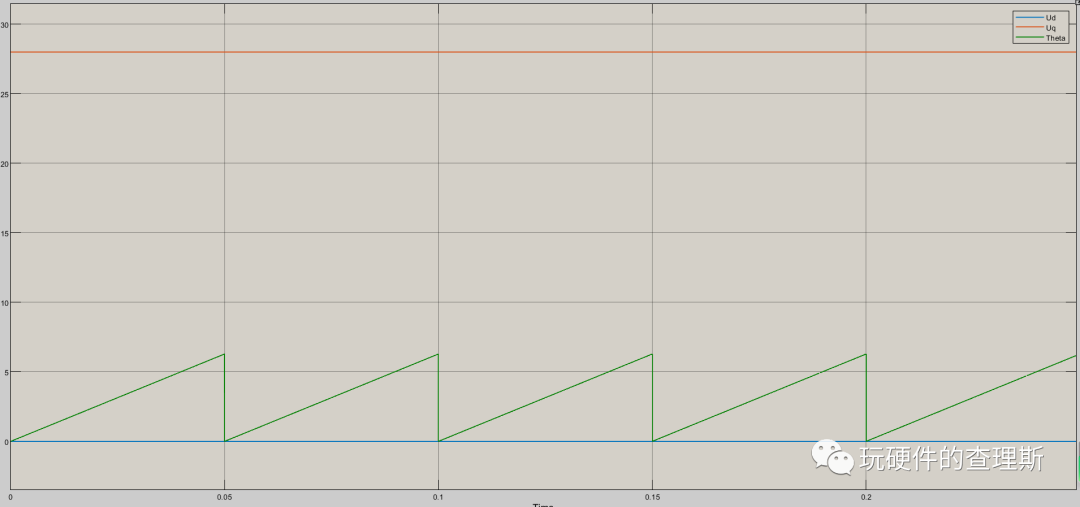
（Ud、Uq、角速度给定值）

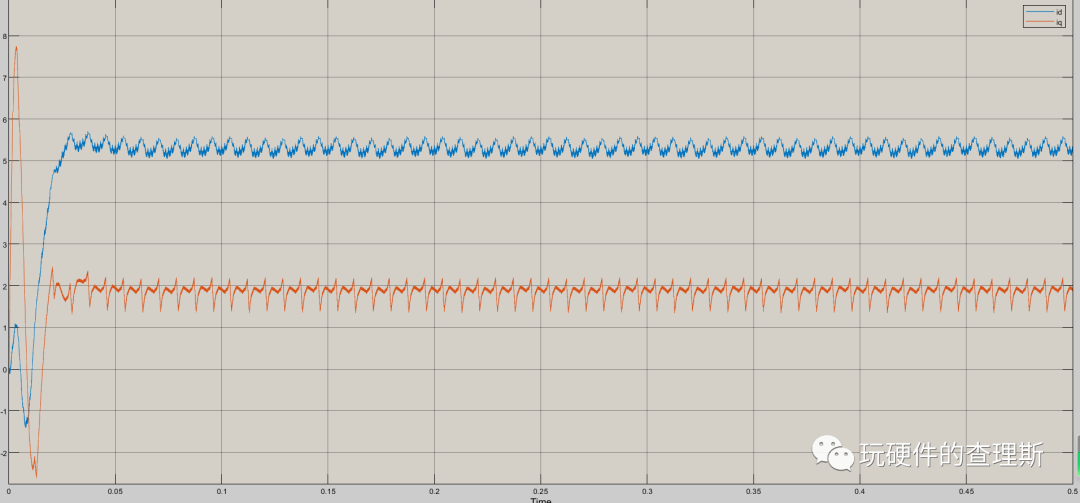
（Id、Iq反馈值）

***四、七段式与五段式对比 ***

在SVPWM 方案中有基于软件模式（七段式算法）和硬件模式（五段式算法)，其中零矢量的穿插是最具灵活性的。

五段式每个Tpwm仅在中间段插入零矢量，每个周期相比七段式减少了1/3的开关次数，减缓了开关器件在负载电流较大时开关动作损耗。

对于七段式SVPWM 算法而言，基本矢量作用顺序为：在每次开关状态转换时，只改变其中一相的开关状态，且零矢量在时间上平均分配，产生的PWM 对称，还能够降低PWM的谐波分量。

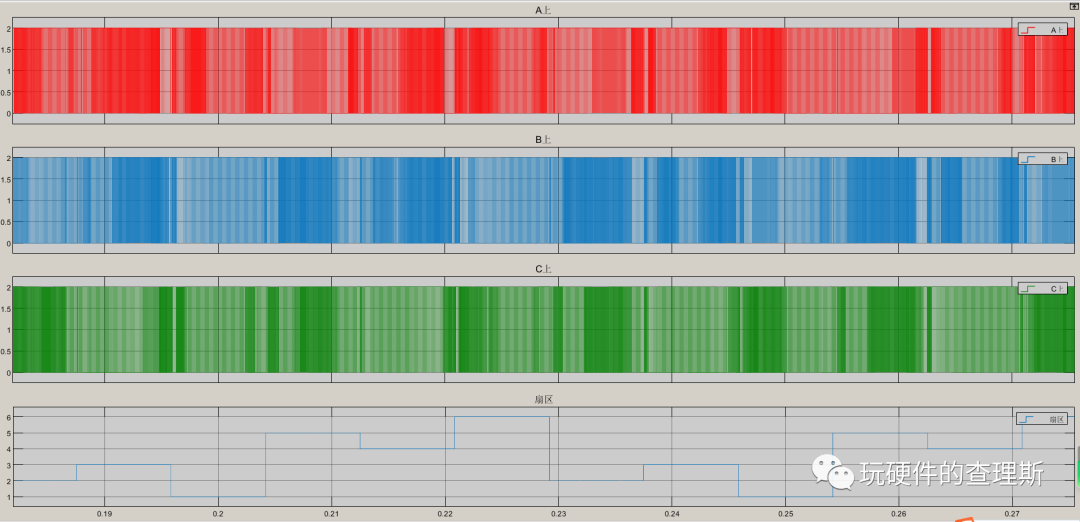
（七段式三相驱动）

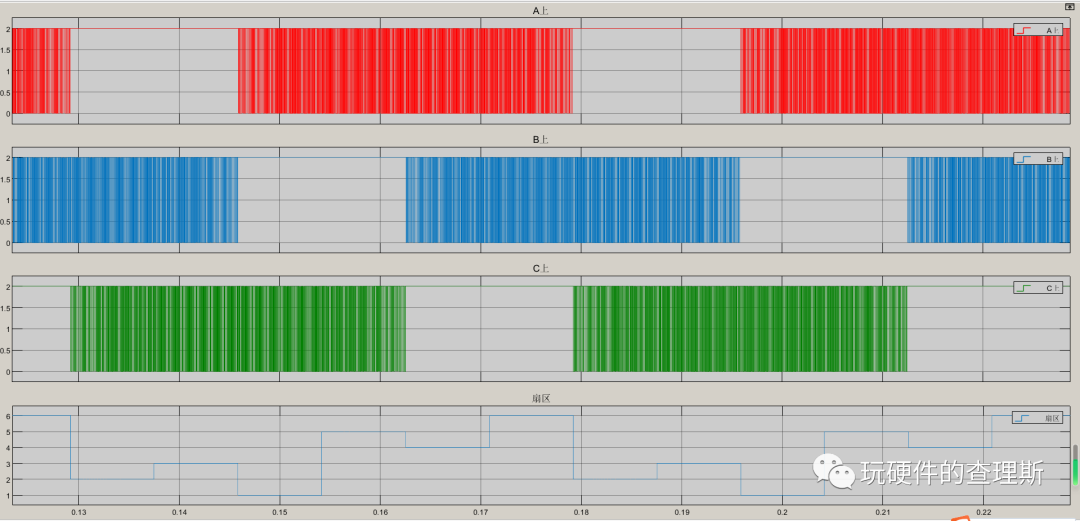
（五段式三相驱动）

（七段式相电流）

（五段式相电流）

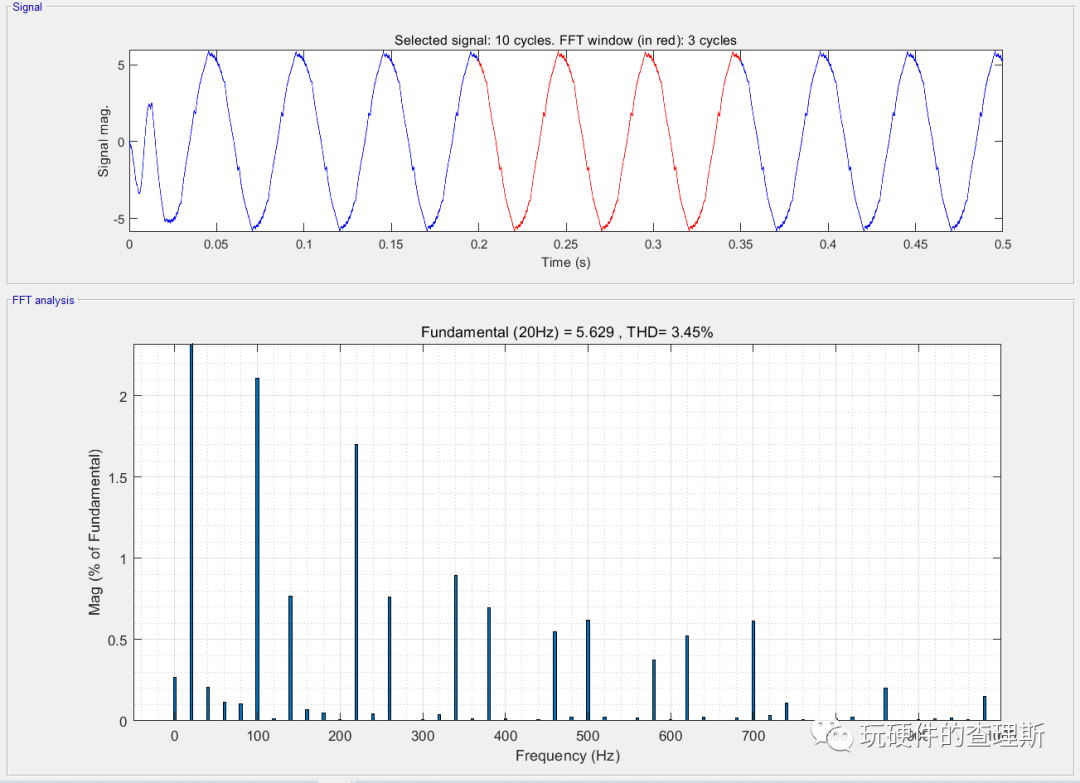
（七段式谐波含量）

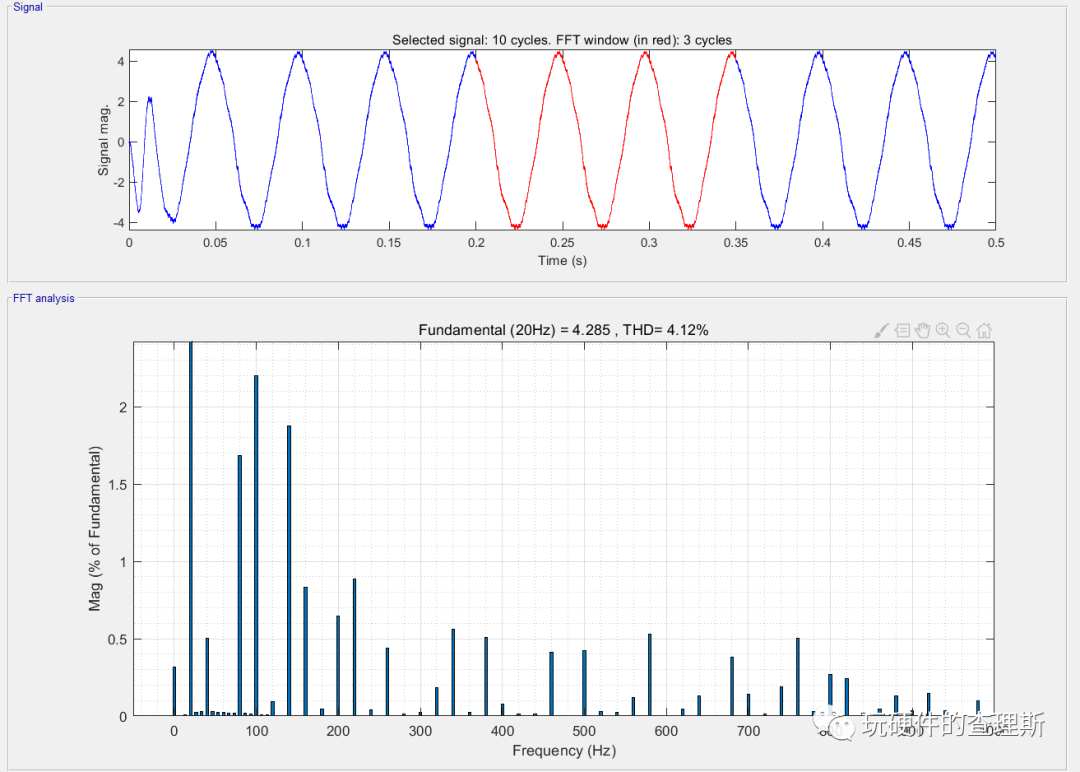
（五段式谐波含量）

从仿真数据中我们可以明显对比出，五段式的驱动波形在每个扇区总有一相的开关管不动作得以休息，相比七段式可减少1/3的开关损耗。

但由于扇区间的衔接是不对称的，所以相电流的波形相比七段式波动更明显，从频谱分析中我们也明显可以对比出，七段式的3次谐波含量为3.45%，而五段式的3次谐波含量为4.12%。

从开环模型的仿真结果来看，五段式算法切合实际的应用，七段式的算法受限于开关元件的性能但有利于更理想的电机运转，可以按应用场景进行选择。

** 总结** ：本次开环仿真也是基于最基本的Svpwm算法搭建，所用的参数及模型均为理想值，对于实际应用仅作为参考价值。