是测试系统的宝贵工具。然而，这些设备的有限方向性可能会导致测量不确定性。本文将详细介绍。

在许多微波和毫米波系统中起着重要作用。例如，矢量网络分析仪（VNA）使用来分离和采样往返于DUT端口的前后波。在本文中，我们将讨论耦合器的方向性系数如何在测量反射功率时引入误差。

测量反射功率

图1展示了一个通用的定向耦合器，用于测量未知终端的反射功率。由于我们测量的是反射功率，因此耦合器的负载端（端口1）被标记为输入端口，即使源端连接到端口2。

使用定向耦合器测量反射功率。显示了所有四个端口，但隔离端口已端接。

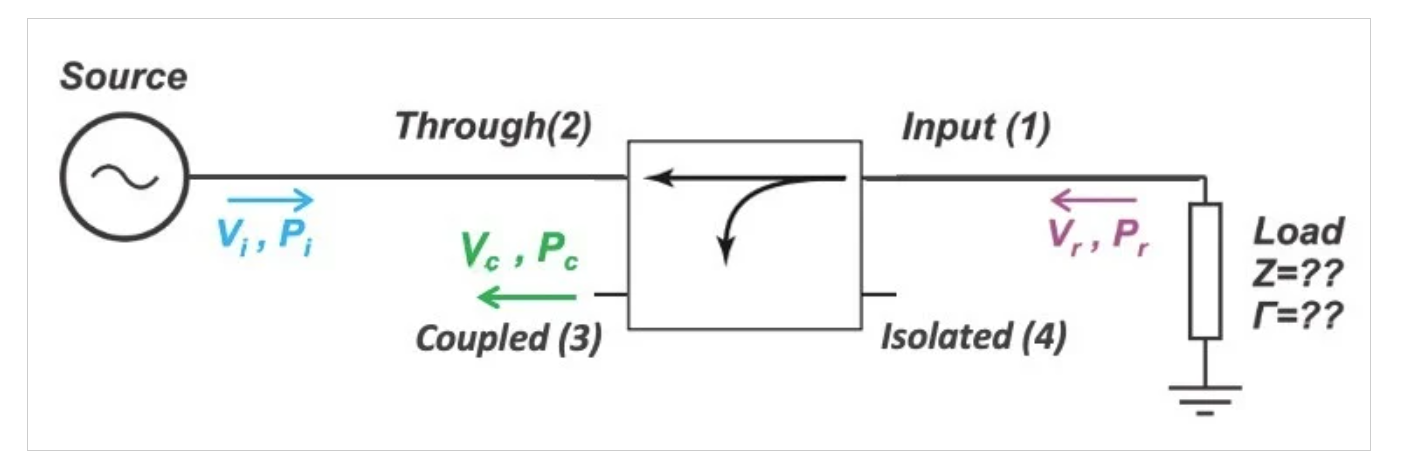
图1.使用四端口定向耦合器测量反射功率。图片由Steve Arar提供

电源提供的功率（Pi）通过耦合器传输到负载——从端口2到端口1。在负载处，一部分功率被反射回耦合器。反射功率（Pr）的量是负载阻抗和互连特性阻抗之差的函数。Pr的一小部分通过耦合器传输，并通过耦合端口端口3退出。

在理想世界中，知道Pi并测量耦合功率（Pc）将使我们能够确定负载反射系数（Γ）。例如，如果负载完全匹配，则没有功率被反射，因此Pc理论上应为零。

然而，现实世界中的定向耦合器会将端口 2 上入射的 Pi 泄漏到耦合端口 3，这会影响功率测量的准确性。泄漏量取决于耦合器的方向性。在本文的其余部分，我们将研究如何量化此误差。

定向耦合器方程综述

在本系列的前一篇文章中，我们介绍了通常用于表征定向耦合器的三个因素：

耦合系数（C）。

方向性系数（D）。 

隔离系数（I）。

对于图1中的四端口定向耦合器，我们可以计算出这些量如下：

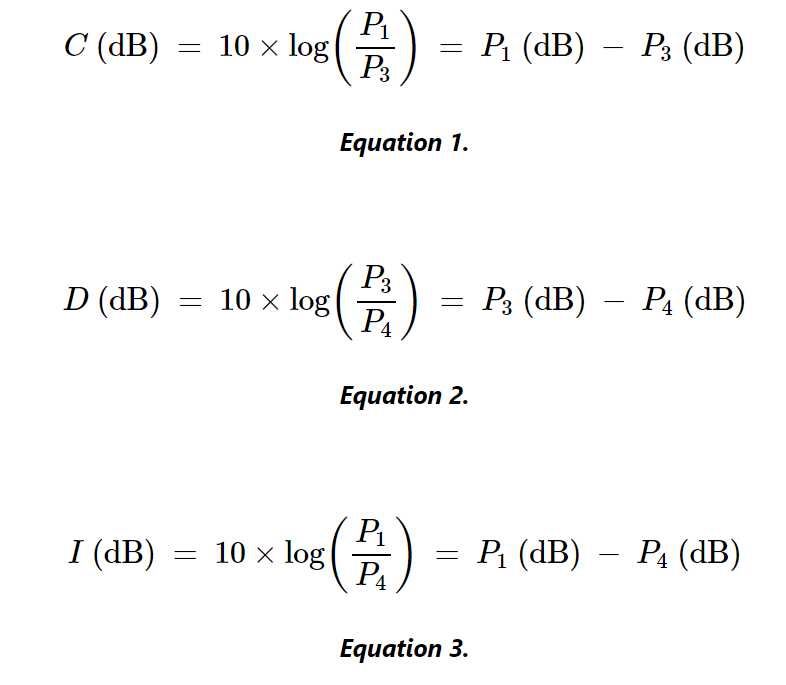
方程式1 方程式2 方程式3 

Px是港口x的功率，单位为瓦特。

Px（dB）是端口x的功率，单位为dB。

这三个因素之间存在有趣的关系：

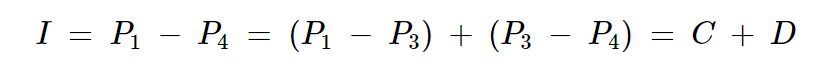
方程式4

计算耦合端口处的反射功率

首先，我们将计算到达耦合端口3的理想功率。假设来自源（Pi）和入射到端口2的所有功率都从端口1流出。从负载（Pr）反射的功率（dB）等于入射功率（Pi）减去负载的回波损耗（RL）：

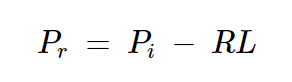
方程式5

端口1上输入功率的一部分被耦合到端口3。通过重新排列方程2，我们可以表示端口3的耦合功率为：

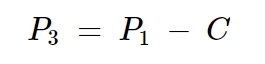
方程式6

我们将端口 3 的耦合功率称为 Pc1。现在，通过将 Pr 替换为 P1，我们得到：

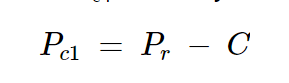
方程式7

最后，将方程5代入方程7，得到：

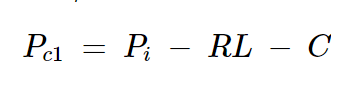
方程式8

图2显示了功率项、耦合因子和回波损耗之间的关系。

定向耦合器的功率项、耦合因子和回波损耗之间的关系。

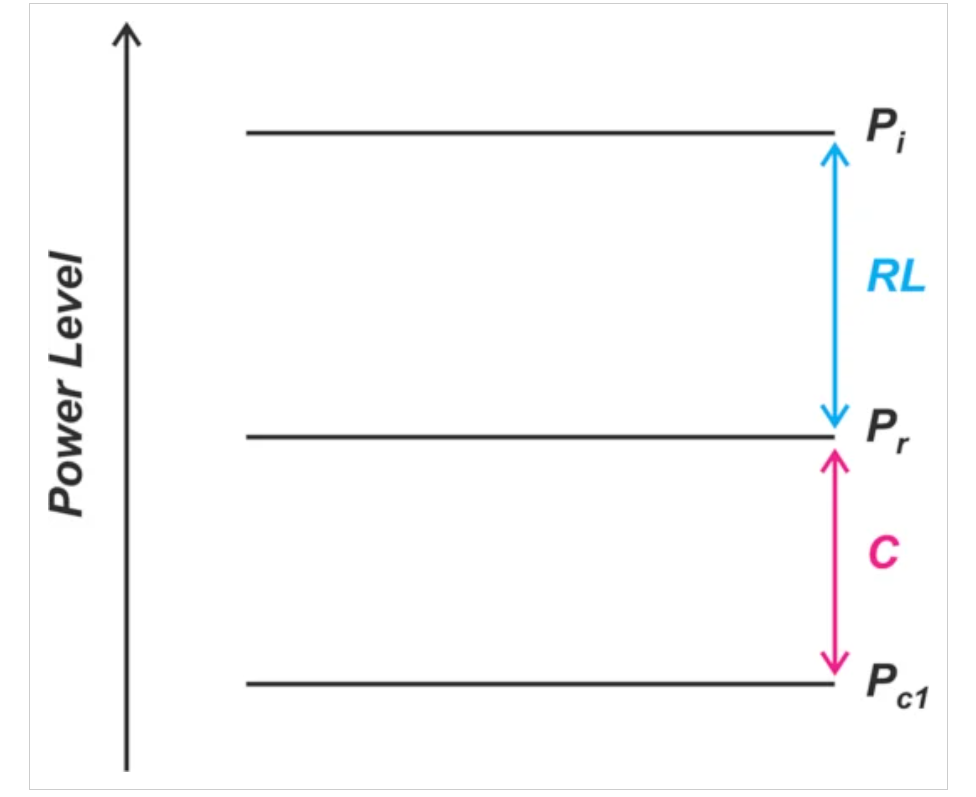
图2:功率项、耦合因子和回波损耗之间的关系。图片由Steve Arar提供

多重反射让事情变得更加困难！

在此分析中，我们假设从负载反射并通过耦合器的功率被耦合器的输入端口（端口1）完全吸收。在实践中，该端口可能不是完全匹配的。因此，耦合器和负载之间可能发生多次反射，进一步改变了测量误差。

有限方向性引起的功率测量误差的计算

现在我们需要开始考虑耦合器中的误差来源。由于耦合器具有有限的指向性，因此Pi的一小部分也会泄漏到端口3。我们将这种泄漏称为Pc2。

对于入射到端口2的波，端口3是隔离端口。因此，泄漏量由隔离因子表征，其方程略有不同：

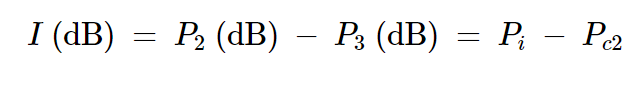
方程式9

重新排列这个方程并代入方程4，我们得到：

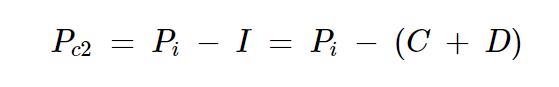
方程式10

图3显示了这组关系。Pc1是指定负载回波损耗的期望信号，Pc2是从端口2泄漏到端口3的信号。

反射功率测量中耦合功率和泄漏功率的关系。

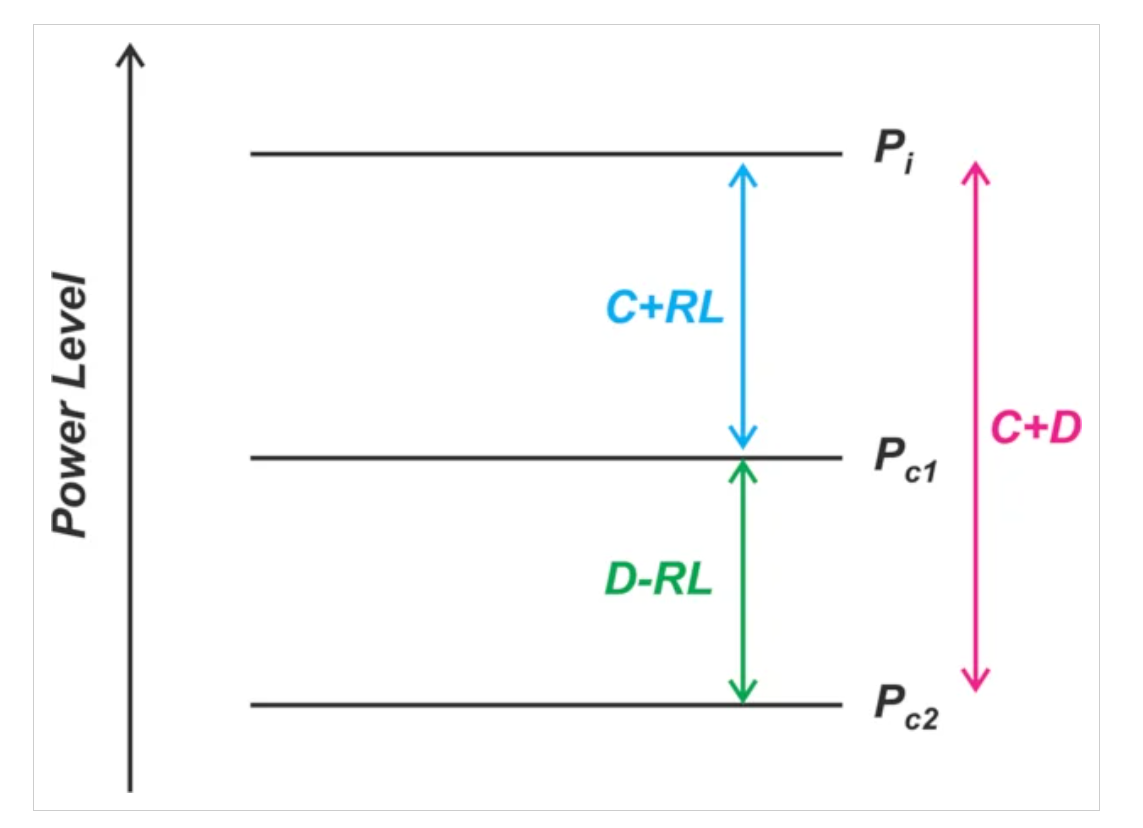
图3.反射功率测量中耦合功率和泄漏功率的关系。图片由Steve Arar提供

Pc2的存在仅是因为耦合器的有限方向性。理想情况下，方向性（D）将是无限的，测量的功率将仅是负载反射功率的函数。当D有限时，在耦合端口出现额外的功率项（Pc2），影响我们的测量精度。

如图3所示，Pc1和Pc2之间的差值等于D – RL。考虑到方向性和回波损耗，我们可以很容易地确定Pc2相对于所需功率有多小。例如，如果D = 34 dB，RL = 26 dB，我们知道Pc2比Pc1低8 dB。

考虑相位差

上文中，我们确定了所需功率测量值（Pc1）与不希望泄漏（Pc2）之间的关系。然而，在耦合端口测量的总功率还取决于这两个信号分量之间的相位差。

假设与Pc1和Pc2对应的电压信号分别是振幅为a和b的正弦波形。使用图3中所示的关系，我们有：

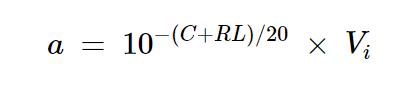
方程式11

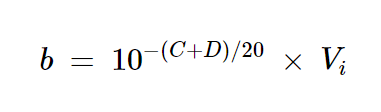
方程式12

其中Vi是图1中电源入射电压的振幅。

如果两个信号同相，则总信号幅度为+b。另一方面，如果两个信号相位相差180度，则总幅度为-b。这两个极端情况给出了总信号的最大值和最小值——相位差的其它值产生的幅度介于a-b和a+b之间。

耦合端口处的总电压波可以表示为：

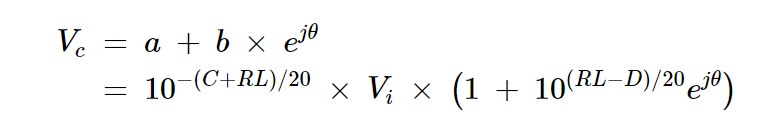
方程式13

方程式13中的术语可以理解为：

ejθ这一术语表示两个信号之间的相位差。

括号内的术语是误差系数，表示测量值与实际值的相对偏差。

括号前面的术语表示如果耦合器具有无限方向性，我们将获得的期望幅度。

我们将把这种期望振幅称为Vdesired，并分别写出它的方程式：

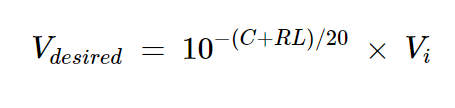
方程式14

然后我们可以将方程式13重写为：

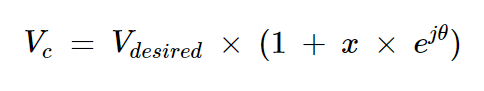
方程式15

其中x等于10（RL-D）/20。总误差因子是1和x的矢量和。图4帮助我们直观地展示了误差项。

误差因子，可视化为具有实部和虚部的向量。

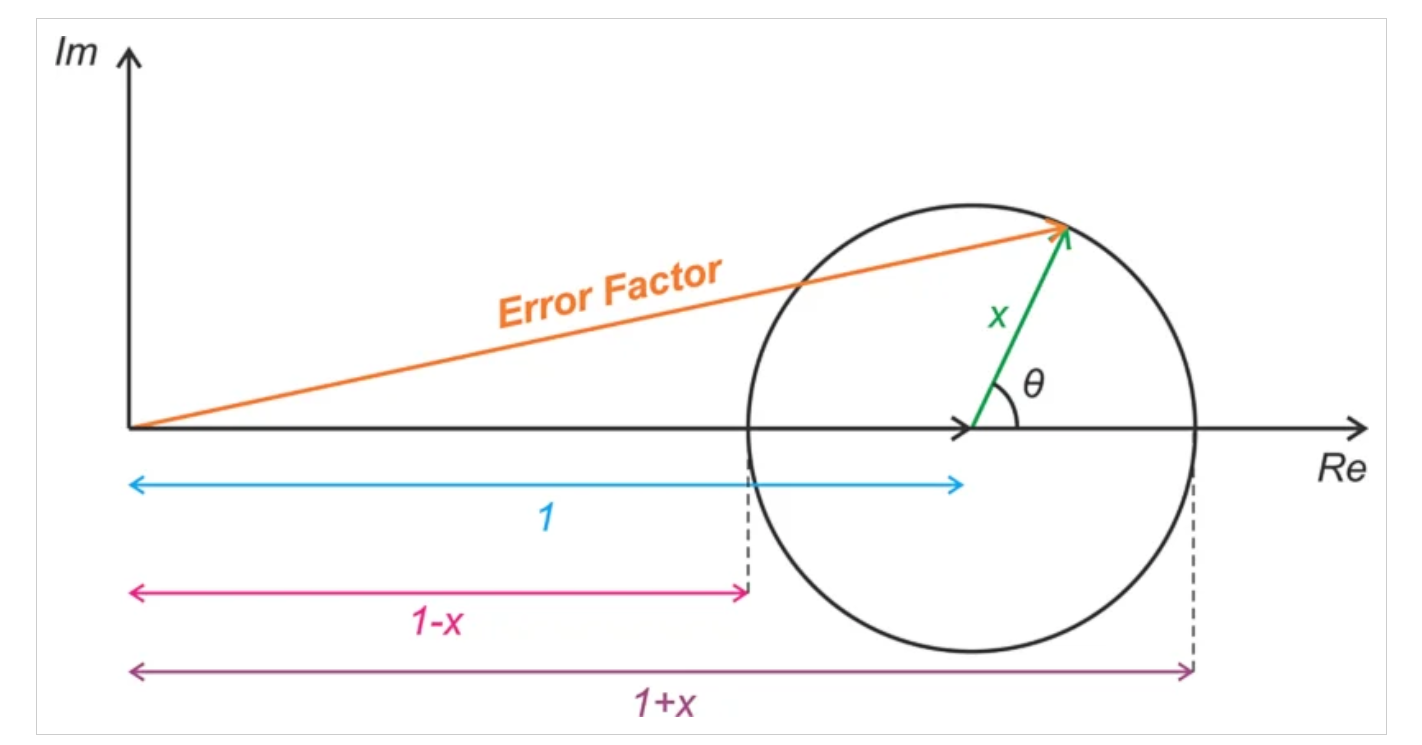
图4.将误差因子可视化为一组具有实部和虚部的向量。图片由Steve Arar提供

示例1：计算测量回波损耗的不确定性

为了澄清上述讨论，让我们来解决罗德与施瓦茨公司关于VNA基础的文档中的一个示例问题。在这个例子中，我们的目标是使用方向性（D）为40 dB的耦合器来测量实际回波损耗（RL）为30 dB的负载。测量的回波损耗的最大值和最小值是多少？

从图3中，我们知道所需信号功率和不想要的信号功率之间的差值等于D – RL = 40 - 30 = 10 dB。因此，不想要的电压的幅度比所需的电压小0.32倍，计算如下：

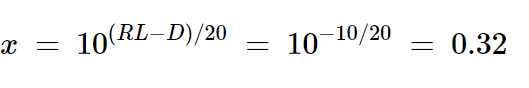
方程式16

将x的这一值代入方程式15，我们看到总电压可以为：

系数1+x=1.32，比实际值高。

系数1-x=0.68，低于实际值。

因此，测量的功率可以是：

20log(1.32) = 比实际值高2.4 dB。

20log(0.68) = 比实际值低3.35 dB。

测量的反射功率与负载的回波损耗有关。反射功率越高，回波损耗越小。当测量的反射功率比实际值高2.4 dB时，测量的回波损耗比实际值低2.4 dB。这导致：

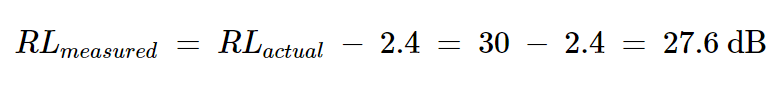
方程式17

同样，当测量的反射功率比实际值低3.35 dB时，测量的回波损耗为30 + 3.35 = 33.35 dB。因此，测量的回波损耗可以在27.6 dB和33.35 dB之间。

示例2：计算测量回波损耗的不确定性

为了更好地理解这些计算，让我们来看另一个例子。假设我们的目标是使用方向性为35 dB的方向耦合器来测量实际回波损耗为20 dB的负载。按照与上述示例类似的过程，我们首先找到不期望电压的幅度相对于期望电压有多小：

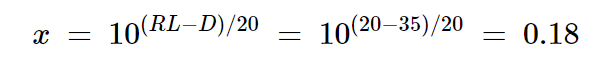
方程式18

总电压可以是：

比实际值高1 + 0.18 = 1.18倍。

系数1 - 0.18 = 0.82，低于实际值。

因此，测量的功率可以是：

20log(1.18) = 比实际值高1.44 dB。

20log(0.82) = 比实际值低1.72 dB。

当测量的反射功率比实际值高 1.44 dB 时，测量的回波损耗为 20 – 1.44 = 18.56 dB。另一方面，当功率测量为低 1.72 dB 时，测量的回波损耗为 20 + 1.72 = 21.72 dB。因此，测量的回波损耗可以在 18.56 dB 和 21.72 dB 之间。

误差如何随回波损耗和方向性变化？

图5显示了不同回波损耗和方向性值下反射功率测量误差。

反射功率测量误差是回波损耗和方向性的函数。

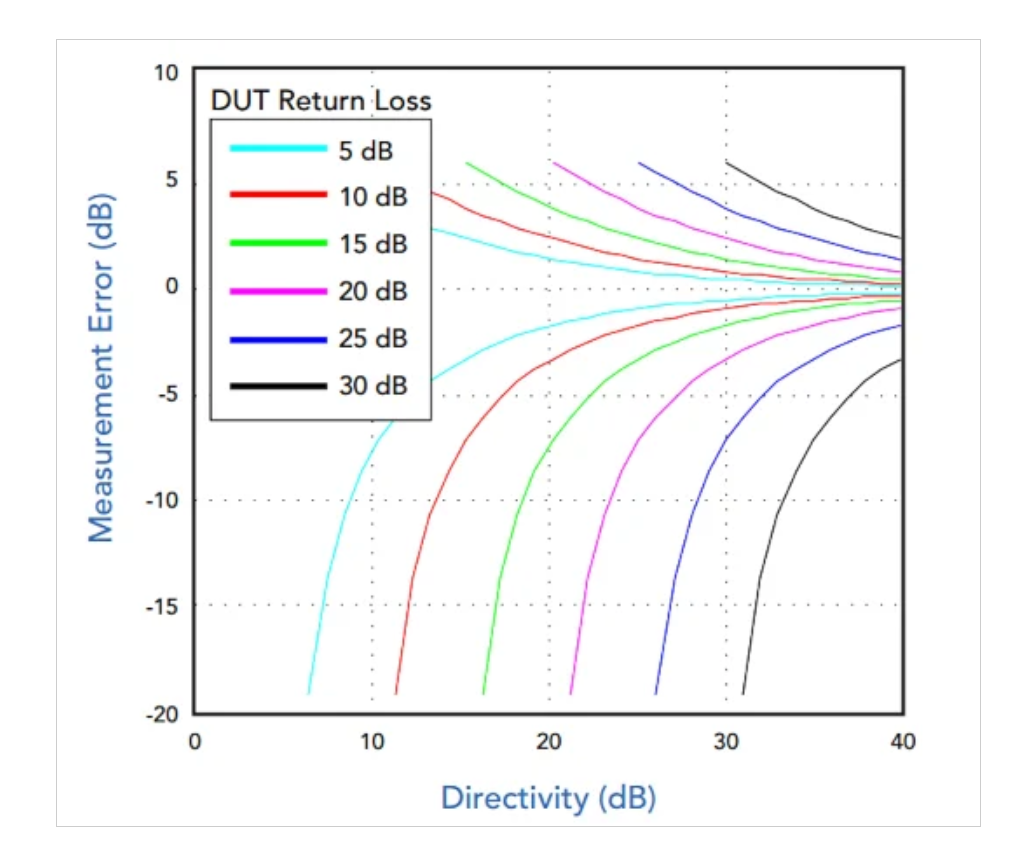
图5.反射功率测量误差与回波损耗和方向性的关系。图片由Marki Microwave提供

上述曲线对应于插入损耗为1 dB的耦合器。这使得结果与我们的分析结果略有不同，在我们的分析中忽略了耦合器的插入损耗。然而，该曲线揭示了有限方向性引入的误差的一些重要特性。

首先，请注意，误差随着回波损耗的增加而增加。对于给定的输入功率（Pi），泄漏功率是恒定的，但测量的信号（Pr）在减小。

其次，观察到增加给定回波损耗的指向性可以减小误差。图3中的关系解释了为什么：随着D的增加，与期望信号相比，不期望信号变得越来越小，从而提高了测量精度。

图5摘自Marki Microwave的白皮书，标题为“方向性和VSWR测量：了解回波损耗测量”，显示了当方向性几乎等于负载的回波损耗时误差会变得非常大。白皮书建议，作为经验法则，您可以通过使用比DUT回波损耗高约15 dB的方向性将误差降低到约1 dB。例如，如果回波损耗为20 dB，我们需要35 dB的方向性将误差限制在1 dB。

测量正向功率

我们还可以使用定向耦合器来对正向功率进行采样，如图6所示。

使用三端口定向耦合器对正向功率进行采样。

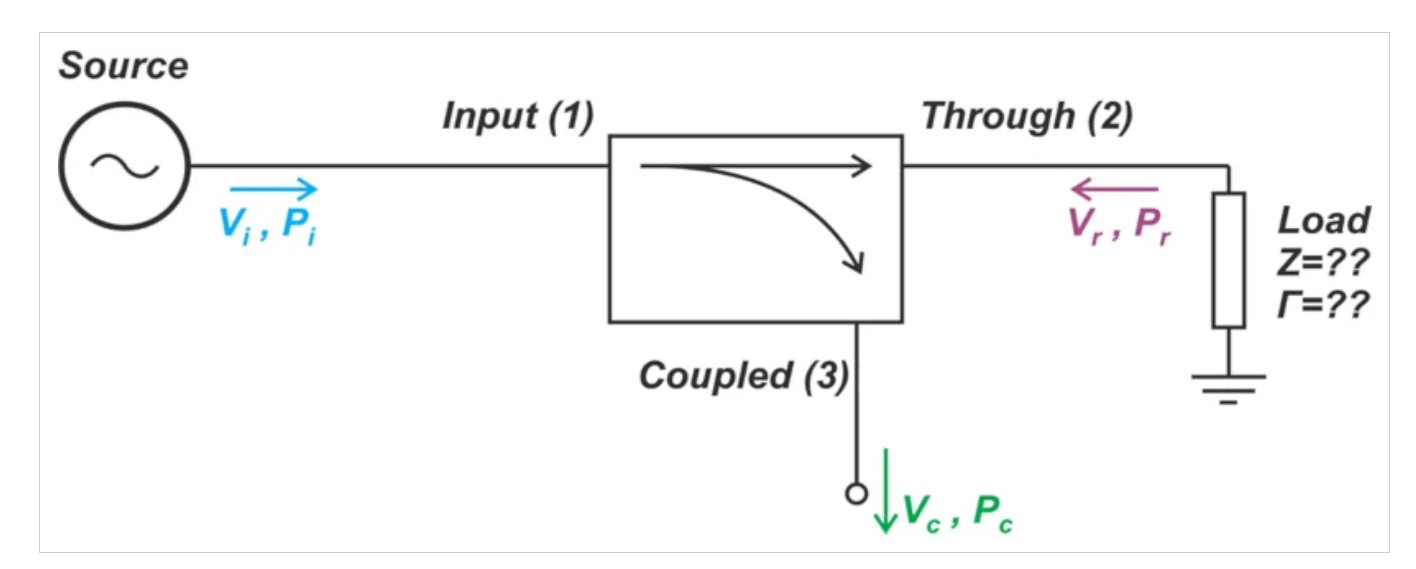
图6.使用三端口耦合器对正向功率进行采样。图片由Steve Arar提供

与反射功率测量相比，耦合器对正向功率测量的方向性要求更宽松。这是因为被测量的输入功率（Pi）大于反射功率（Pr）。图7显示了不同回波损耗和方向性值的前向功率测量误差。

正向功率测量误差是回波损耗和方向性的函数。

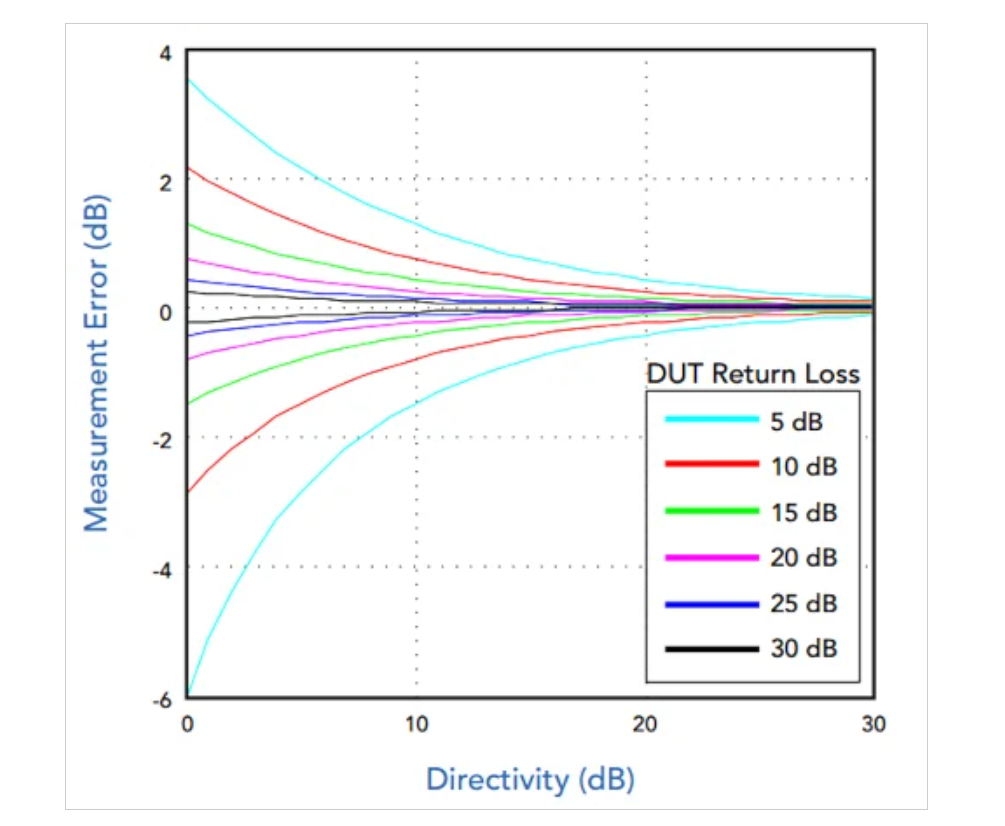
图7. 正向功率测量误差与回波损耗和方向性的关系。图片由Marki Microwave提供

请注意，负载回波损耗越小，误差就越大。这是因为较低的回波损耗意味着更多的功率被反射回源。这反过来导致耦合器输出端的不期望信号增加。即使对于很小的回波损耗，15 dB的指向性也可以确保正向测量的误差不超过大约1 dB。

耦合器方向性的测量

最后，由于它与本文中提供的误差分析密切相关，我想提一个测量耦合器方向性的实用方法。我们通常不能直接测量这个方向性，因为前向和后向波在耦合器的输出端产生了可比较的信号分量。

然而，我们可以修改图1，使用滑动负载间接测量耦合器的方向性，如图8所示。

测量耦合器方向性的电路。

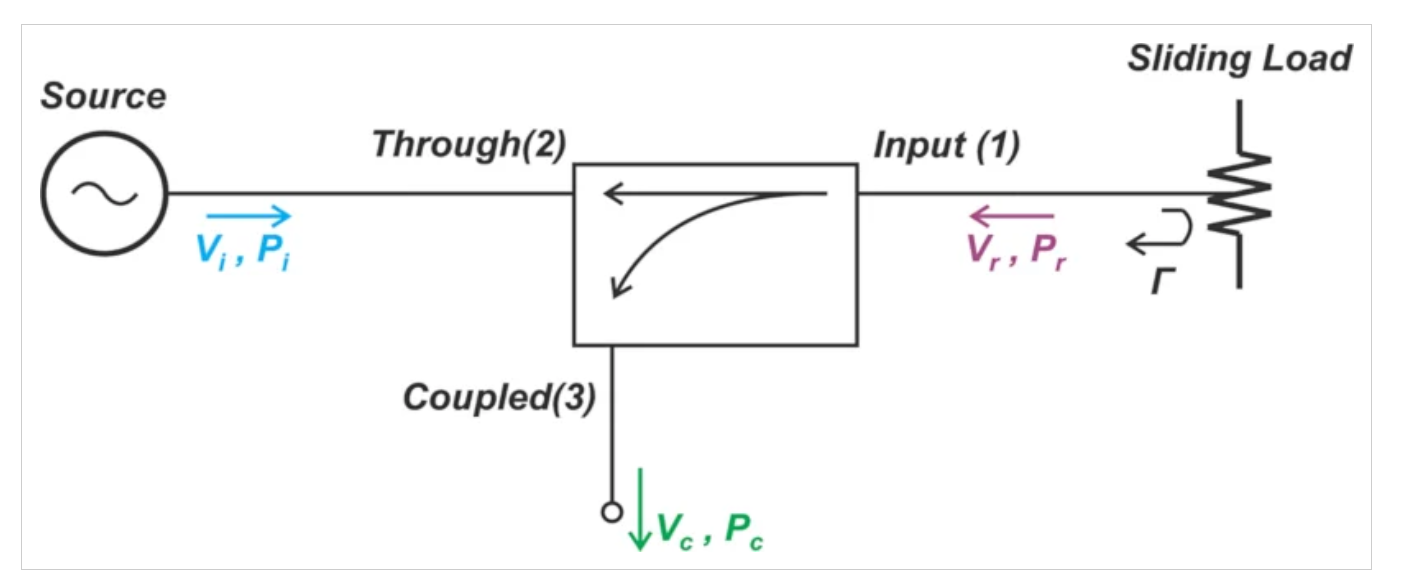
图8.测量耦合器方向性的电路。图片由Steve Arar提供

改变滑动负载的位置会在反射信号中引入可变相移。根据我们上面的讨论，我们知道，当我们改变滑动负载的位置时，耦合端口处的电压会产生圆形轮廓（图4）。通过找到耦合端口处的最小和最大功率电平，我们可以确定耦合器的方向性。