组成自动驾驶的关键技术包括感知、规划和控制三大部分。自动驾驶车通过传感器感知环境并进行定位，根据感知系统获得的信息和行驶目标进行速度和路径的规划，并以控制系统为基础实现车辆的运动控制。

背景

导航是感知系统下重要的模块，其性能优越程度决定了自动驾驶的性能。基于扩展卡尔曼滤波器的GNSS/SINS松耦合组合是最常见的导航算法之一，但是此算法对GNSS的鲁棒性极低，不适用于狭窄的道路。另一个重要的方法是车道检测和跟踪。一种是基于霍夫变换表示的视觉，但这种方法要求路面高度清洁。另一种基于激光雷达，通过获取雷达扫描点的坐标并将其转换为光栅图像，然后利用光栅图像中的点密度提取车道线。

规划系统的经典形式是比例积分微分（PID）控制器，它不需要系统模型，并且基于误差信号设计了控制率。但当路径的曲率较大时，跟踪精度会降低。另一种典型的方法是基于车辆运动学模型。该方法利用车辆运动模型预测一段时间内的未来运动，并通过连续优化的控制参数来拟合这一系列运动，但此方法只考虑重心的偏差和预测时域中的偏差。

在这项研究中，研究人员基于平方根容积卡尔算法（SCKF），以二阶固定非线性展开为测量模型，设计了融合IMU、GNSS接收机和里程表的组合导航控制算法。导航控制算法将预期路线划分为多段，并根据电子地图的经纬度、航向角和关键点序列来进行计算，最终得到无人驾驶车辆与分段路线之间的角度偏差。该算法通过增量式PID控制器消除偏差，实现逐段路径跟踪。仿真实验结果表明，基于SCKF的组合导航算法的精度优于基于SKF的组合导航。该系统的组成如图1所示。

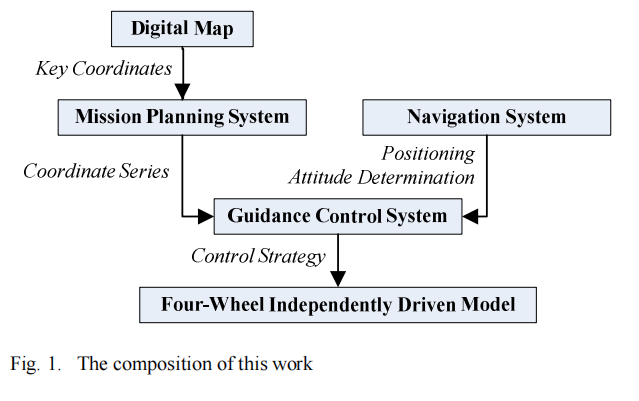
图1

导航系统

基于惯性导航误差模型的滤波器在观测异常时容易出现异常甚至发散。其原因是基于小误差假设建立了组合导航的滤波观测方程。当惯性导航误差变大时，滤波观测方程的线性化过程将不理想。

因此，在本研究中，引入了一种非线性滤波器，立方体卡尔曼滤波器（SCKF），该滤波器使用三阶球面径向体积规则来近似非线性变换中所需的积分运算。为了避免矩阵计算过程中的失真，本文推导了与平方根卡尔曼滤波器相似的立方卡体尔曼滤波器。

最终的推导结果如下，Wk为反馈矩阵，X k|k为最佳状态，Pk|k为方差矩阵。

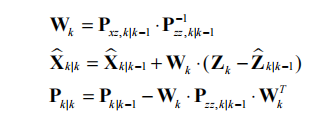
引导算法

引导控制算法基于地图信息和关键点生成坐标序列，并生成用于分段运动控制的引导参数，以根据所建立的路线实现自动驾驶。制导控制算法的体系结构如图3所示。

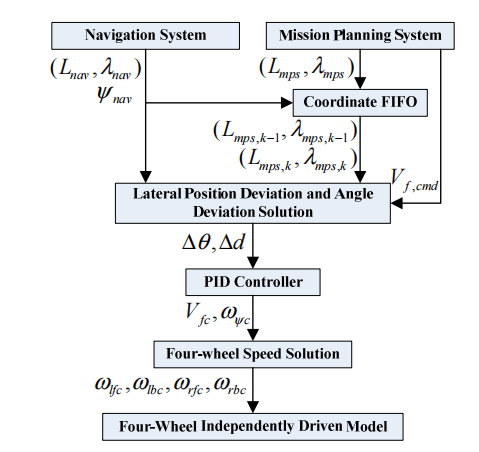
图3

考虑到具有轮距W和车轮半径r的四轮驱动车辆，四轮转向模型如图4所示。

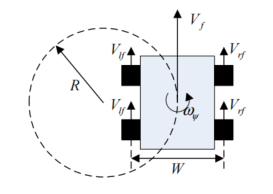
图4

制导参数由航向角偏差d和横向距离偏差r组成。制导参数与关键点坐标序列的关系如图5所示。

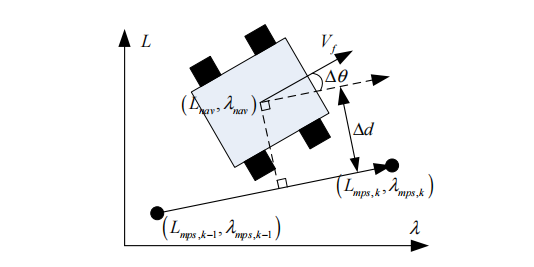
图5

结论

研究人员对该系统进行了仿真测验，结果表明，基于SCKF的组合导航算法的精度优于基于SKF的组合导航。为了验证自动驾驶算法的有效性及其对卫星信号干扰的鲁棒性，进行了无人驾驶汽车的室外自动驾驶实验。该算法是自动驾驶仪的基本形式，具有很高的工程应用价值和参考价值。这项工作缺乏对环境感知的处理，例如障碍物的存在。因此，下一步的研究将集中于在线路径规划和重构。