中学时，提到电阻，会想到阻值和欧姆定律这些等。 提到阻性分析，联想到伏安曲线分析。

电阻在电路中用途很多很广。通常设计产品的时候，负载也许在某种环境下，除了本身的原生特性，还可能会产生其他的特性，如阻性、容性和感性。举例：2020年口罩机的超声波电源和振子，超声波电源就是驱动振子，而振子是感性负载，所以在设计超声波电源的时候，就要考虑到设计的电路和波形是不是会受到这些特性的影响。

阻性分析仿真：（软件：tina-ti），推导出阻性的数学模型。

1、 正弦波在纯阻性分析

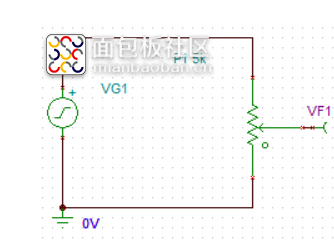
VF2:ui （1V 50HZ ） VF1:uo

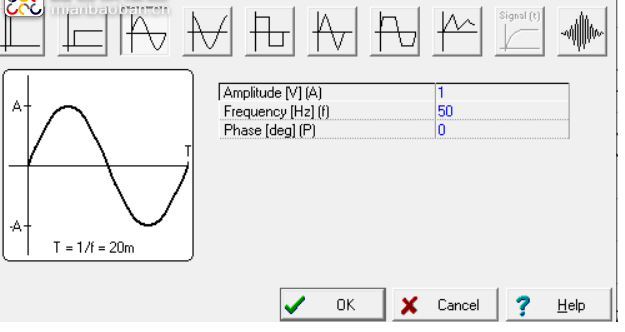
V2（Ui）波形：直流分量为0V，幅度为1V，周期为20ms，以相位由0开始的时域连续周期性函数。

纯电阻电阻比值为50%，即2.5k（0.5W）。

测试波形如下：

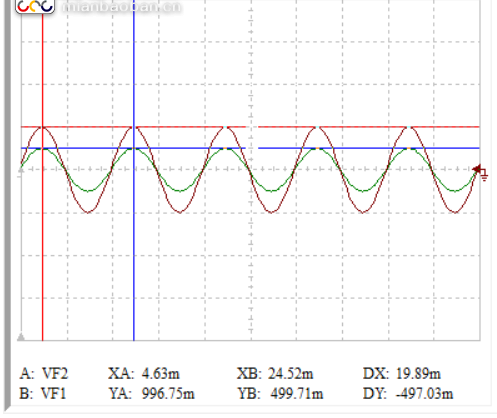
A： VF2:ui VP:1V（996.75m）

B： VF1:uo VP:0.5V（499.71m）

测试结果：纯阻性元件不会影响输入电压波形的相位和波形主要形状，但是会影响波形的幅度，但呈现线性关系。是消耗能量（电能）的性质。

纯阻性的信号分析完毕。

2、高频电阻模型

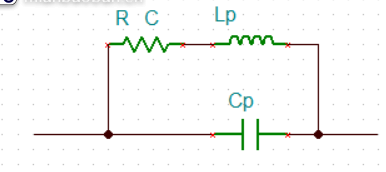
高频的电阻等效模型

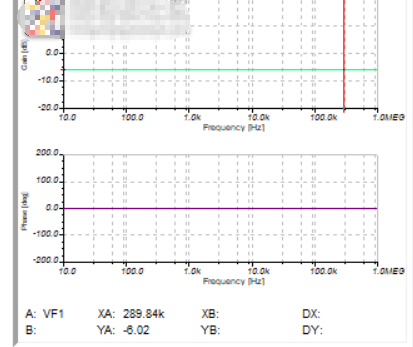
1）50%的阻值比

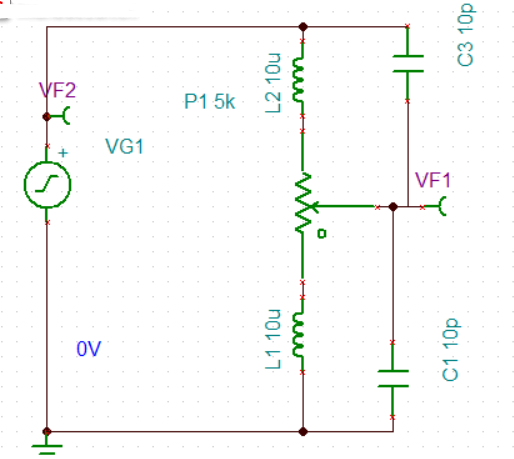
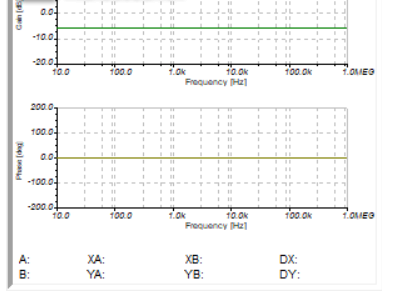
单上下端的电阻值相等和性质一样的时候，（0-1MHZ）波形都是一个非常完美的状态和平衡。

1）20%的阻值比

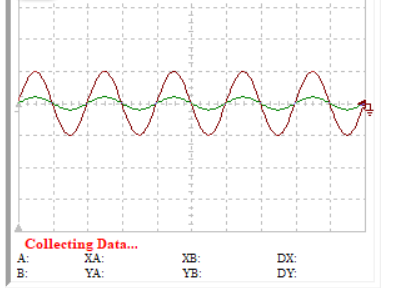
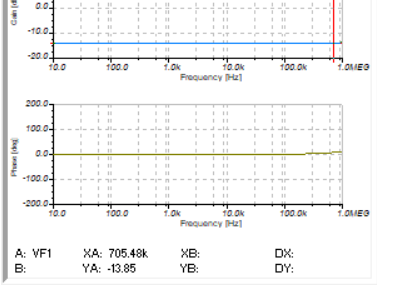
在频率增加的时候，增益增加了，相位超前了。

3）80%的阻值比

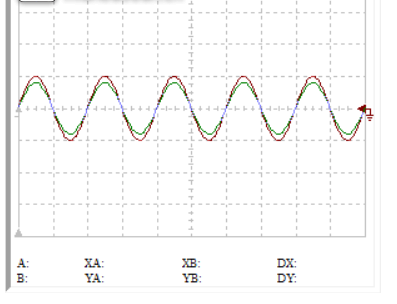
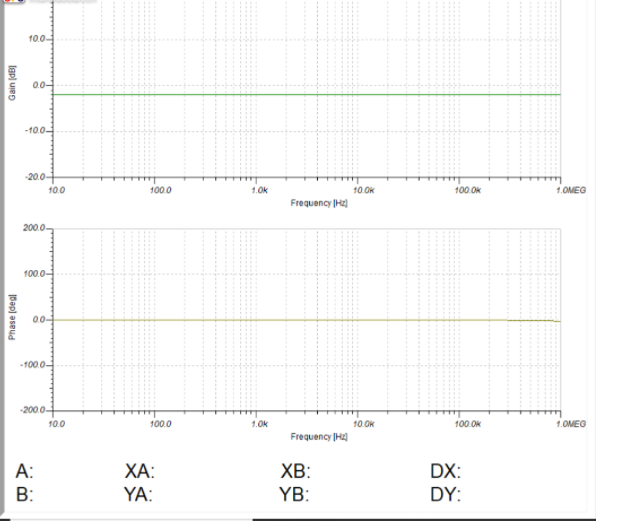
在频率增加的时候，增益增加了，相位滞后了。

测试小结结论

1） 阻值匹配，使得高频信号能等时等长，同时到达（不超前不滞后）

2） 运用阻容器件，可以巧妙进行相位补偿

3） 高阻抗，对于处理小信号，会对噪声有抑制作用

4） 时钟信号和敏感信号线路尽量短，阻值等长

5） 阻性可以吸收波形（如反射）、差分电路阻抗相等等等

这里主要就是推导出阻性在电路的数学模型。

（1） 在相同条件下，1：1的情况下：Uo（t）=p *Ui（t） （P为比例常数，如电阻比值；Ui为输入波形，t为时间）

（2） 在阻抗不一，和频率变化的情况下：Uo（t）= （ p + C ） * Ui（t + ph） （P为比例常数，C为不确定增益常量，Ui为输入波形，ph为不确定相位常量）