与低通或高通滤波器不同，全通滤波器的增益始终存在于其使用的频率范围内，但它确实提供了与频率相关的相移。可以级联多个全通滤波器，以产生用于电子音乐的相位单元。

相位效应是通过对信号进行相移，然后将信号的原始变体和相移变体相加而产生的。图1显示了第一类全通滤波器的基本电子电路。

相移取决于R和C的相对值以及输入频率。在低频时，C具有非常高的阻抗，电路仅用作反相放大器，因此相移为180°。在高频下，C的阻抗很低，电路用作零相移的同相放大器。

滤波器的增益取决于Rl和R2的相对值。在这种情况下，Rl和R2被选择相等，因此增益是统一的。该图显示了填料的相移与频率曲线。

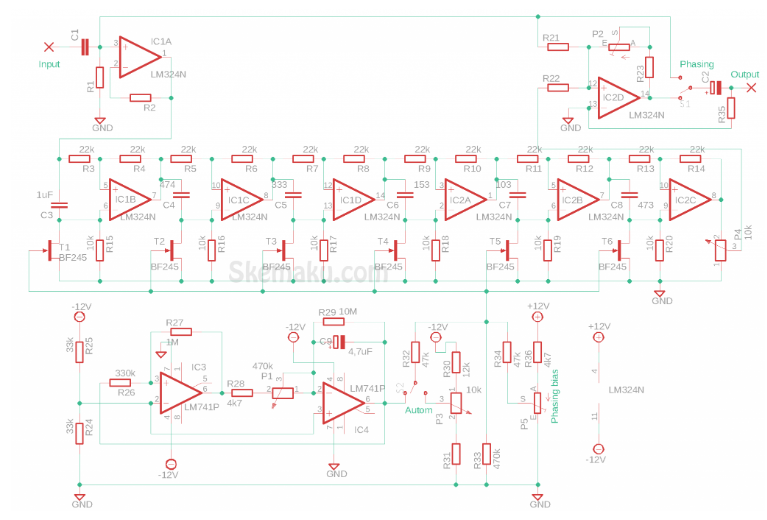
使用所有通滤波器的相位单元的完整电路如图2所示。六个全通滤波器级级联，因此低频下的总相移可达1080“！在电路中使用总共10个运算放大器似乎相当过分，但由于其中8个是LM324四通道运算放大器，因此总封装数量仅为4个IC。

IC1a用作单位增益输入缓冲器，IClb至IC2c是六个滤波器级。直接和相移信号由lC2d求和。相移信号的比例以及相位深度可以利用P4进行调整。

特定频率下的相移程度可以通过FET Tl至T6来改变，FET用作电压控制电阻。通过改变栅极电压，漏源电阻可以增加或减少，从而改变每个全通滤波器中“R”的有效值，从而改变相移。

这可以使用P3手动控制，也可以由IC3和IC4组成的三角波发生器的输出自动上下扫频。由于FET的栅极电压必须始终为负，因此该振荡器的输出在‘2和– 6 V之间摆动。

振荡器频率可以通过PI来改变，最佳相位效果发生在0.5Hz和1Hz之间的频率。在较高频率（约4 Hz）下，相位效果会丢失，但会获得颤音效果。