模型搭建背景

三相永磁同步电机(PMSM)是目前被广泛应用的一种电机，电机本体也是一个强耦合、复杂的非线性系统，matlab电力模块库中已经包含了各种电机本体模型，但是为了能够更好地设计先进的PMSM控制算法,了解电机中各个量的关系，有必要建立一个数学模型。同时，在仿真中，有时候可能会存在有些工况下要求电机具备变参数功能，如果能够自己搭建一个数学模型，这样就可以根据需求更改相关的参数，使用上更加灵活。

目前,根据永磁体转子上的位置不同,三相 PMSM的转子结构可以分为表贴式和内置式两种结构,对于表贴式转子结构而言,由于其具有结构简单、制造成本低和转动惯量小等优点,在恒功率运行范围不宽的三相PMSM和永磁无刷直流电机中得到广泛应用。表贴式转子结构中的永磁磁极易于实现最优设计,能使电机的气隙磁密波形趋于正弦波分布，进而提高电机的运行性能。内置式转子结构可以充分利用转子磁路不对称所产生的磁阻转矩,提高电机的功率密度,使得电机的动态性能较表贴式转子结构有所改善,制造工艺也较简单,但漏磁系数和制造成本都较表贴式转子结构大。

永磁同步电机数学模型

根据坐标系的不同，常见的永磁同步电机电机数学模型可分为基于abc三相自然坐标系下的模型，基于α—β静止坐标系模型以及基于d—q旋转坐标系模型。abc坐标不需要坐标变换，但方程相对复杂，变量较多，耦合度较高计算较为复杂，abc坐标系转换到α—β坐标系统后，模型参数仍存在随时间变化的问题，这些参数的变化使得控制系统设计变得复杂，因此，为了便于后期控制器的设计，通常选择同步旋转坐标系d—q坐标系下的数学模型进行电机模型的建模。

永磁同步电机的数学模型一般可以用如下四个方程进行描述，分别是定子电压方程、定子磁链方程、电磁转矩方程，以及机械运动方程。各方程公式如下：

定子电压方程：

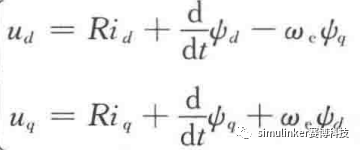
定子磁链方程：

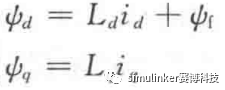
将定子磁链方程带入定子电压方程可得：

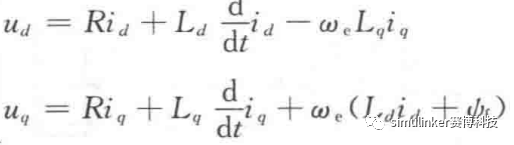
** 电磁转矩方程：**

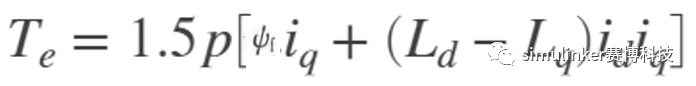
其中，p为极对数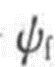，为永磁体磁链

机械运动方程：

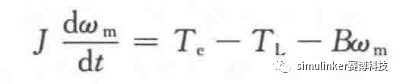
其中，wm为电机的机械角速度;J为转动惯量;B为阻尼系数;TL为负载转矩。

通过上述四个电机的公式，即可完成完整的永磁同步电机数学模型的搭建。

仿真模型

基于上述公式可搭建永磁同步电机数学模型如下：

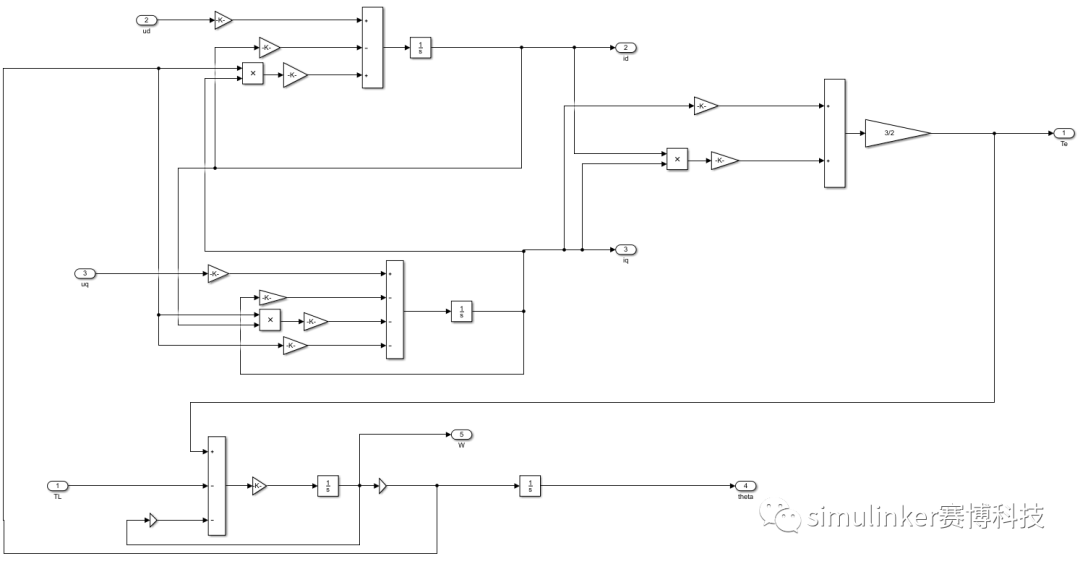
图1 永磁同步电机数学模型

参照matlab自带模块库模型，可将模型进行简单封装，得到基于负载转矩（TL）输入的模型和基于电机电角速度(w,rad/s)输入的模型，其中ud,uq为电机接入点三相电压经dq变换后的信号。由于基于电角速度输入的模型省去了机械运动方程部分，相比基于负载转矩的模型简单，运行时更容易稳定。

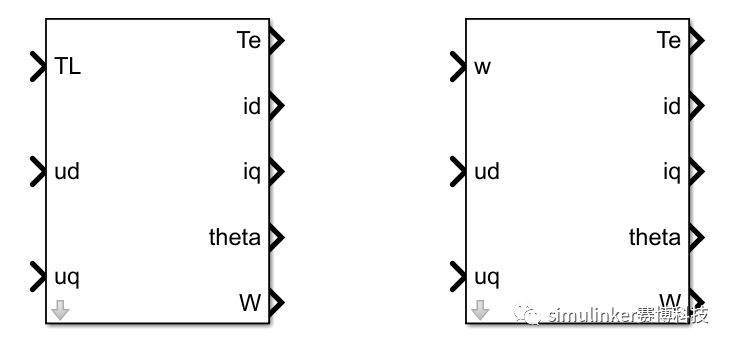
图2 永磁同步电机数学模型封装

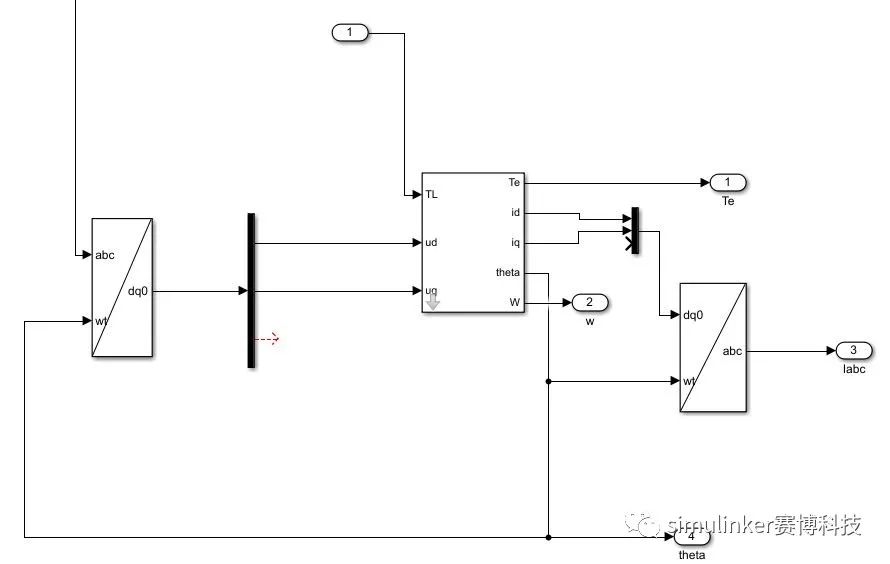
图3 永磁同步电机数学模型封装内部

仿真结果验证

（1）为验证本文所搭建的模型的正确性，搭建电路结构及参数完全相同的简单电路模型，并给定完全相同的负载转矩，进行测试。

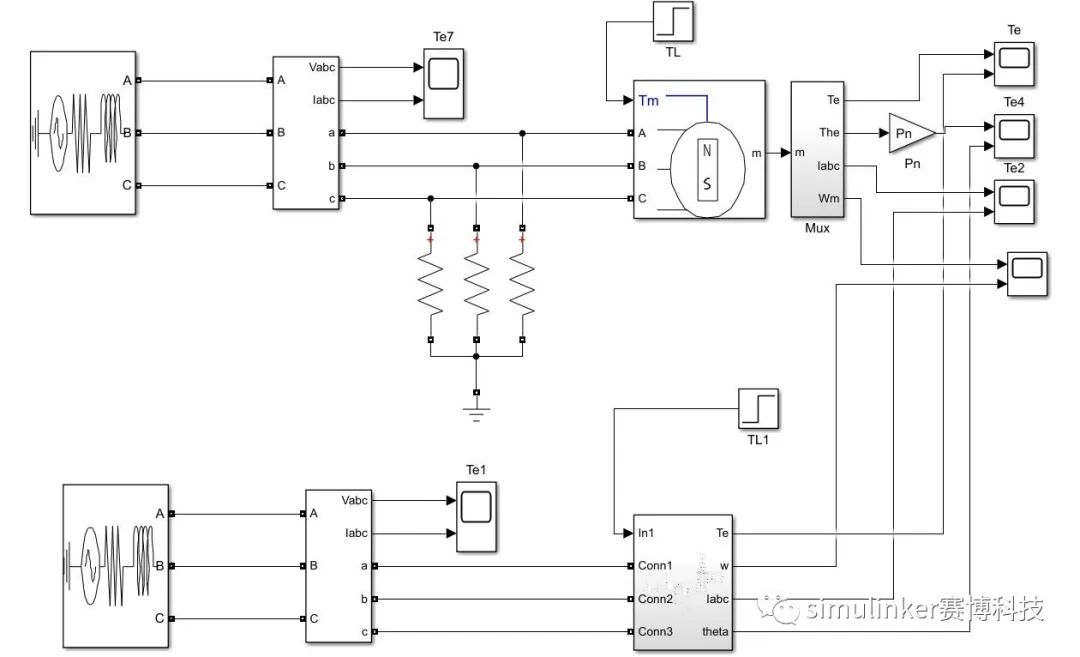
图4 对比测试模型

运行仿真结果如下：

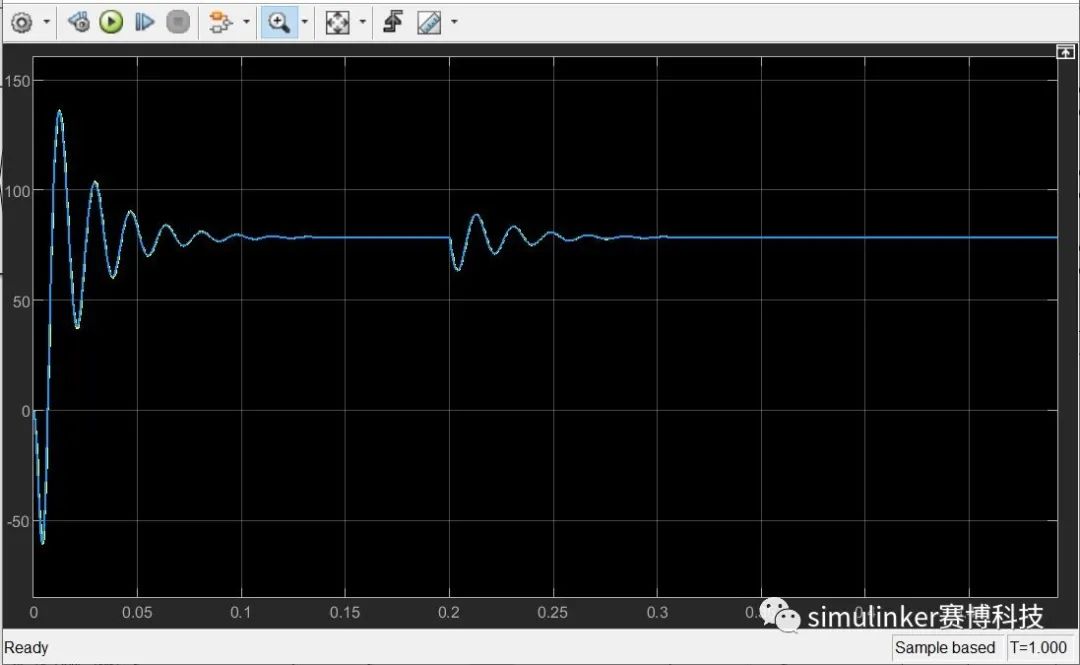
图5 电机输出角速度（rad/s）

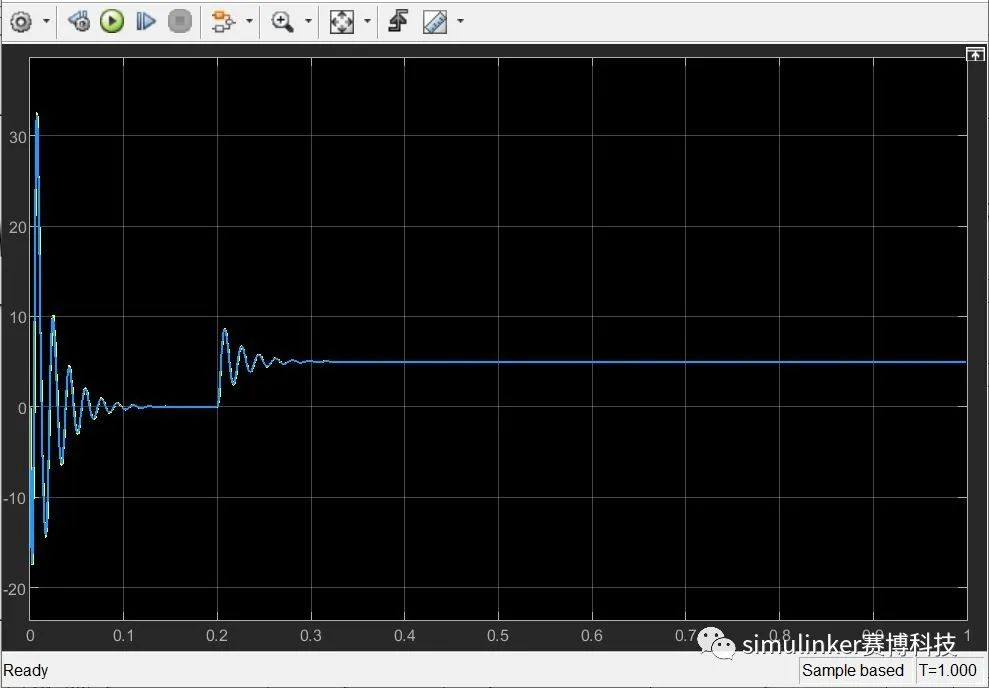
图6 电机转矩波形

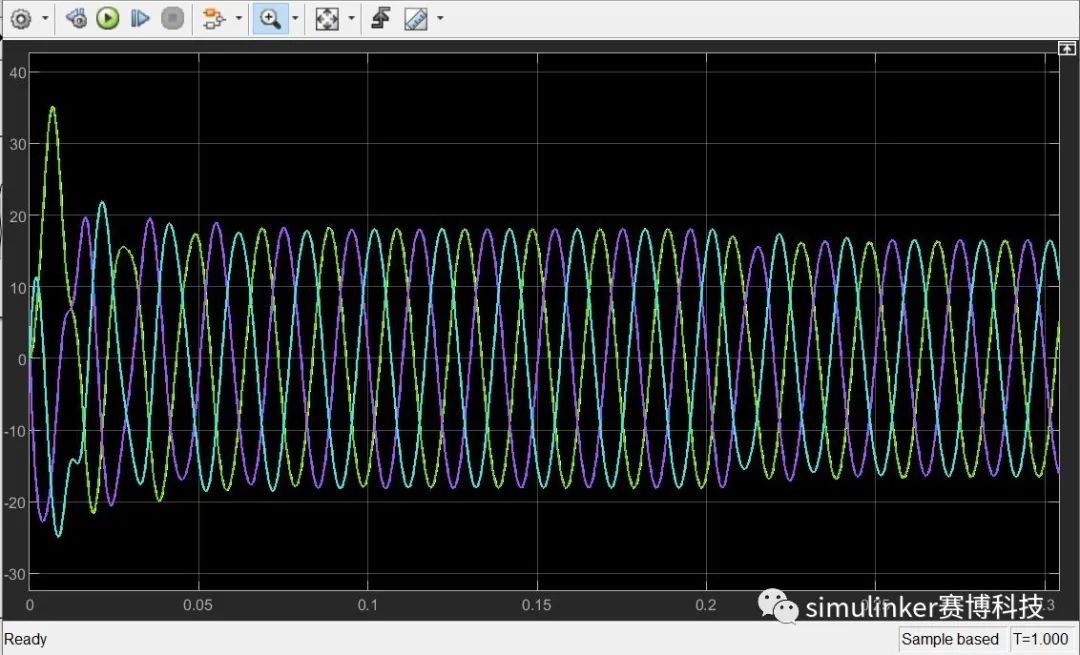
图7 电机电流波形

（2）为进一步验证本文所搭建的电机本体模型，搭建电路结构及参数完全相同的基于FOC控制的永磁同步电机调速控制仿真模型，并给定完全相同的负载转矩及转速指令，进行测试。

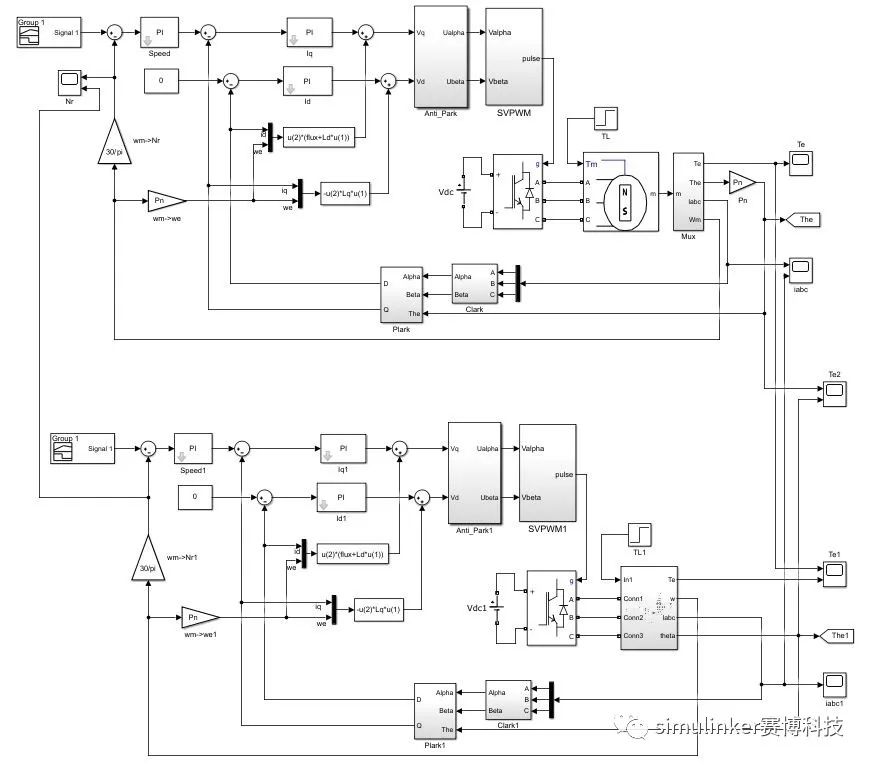
图8 电机调速对比测试模型

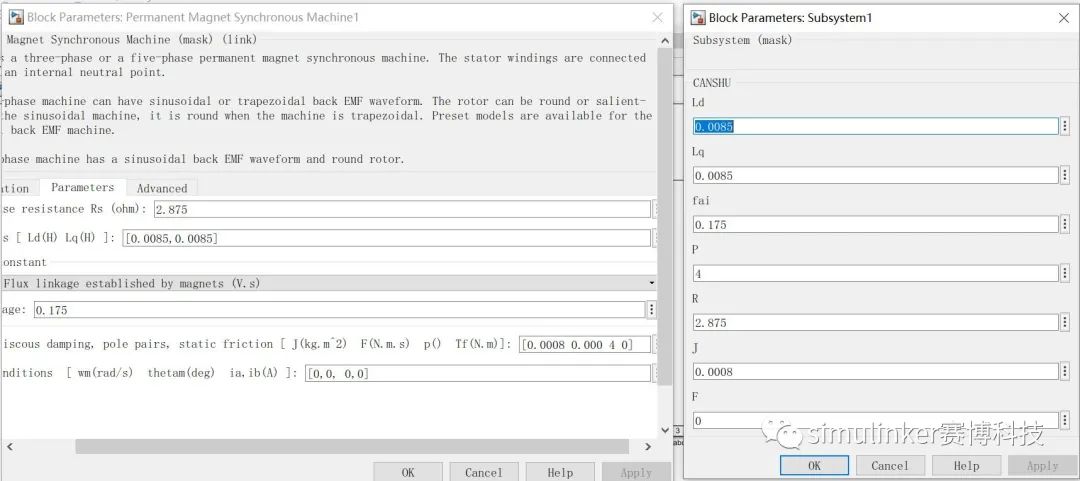
图9 电机参数对比

运行仿真结果如下：

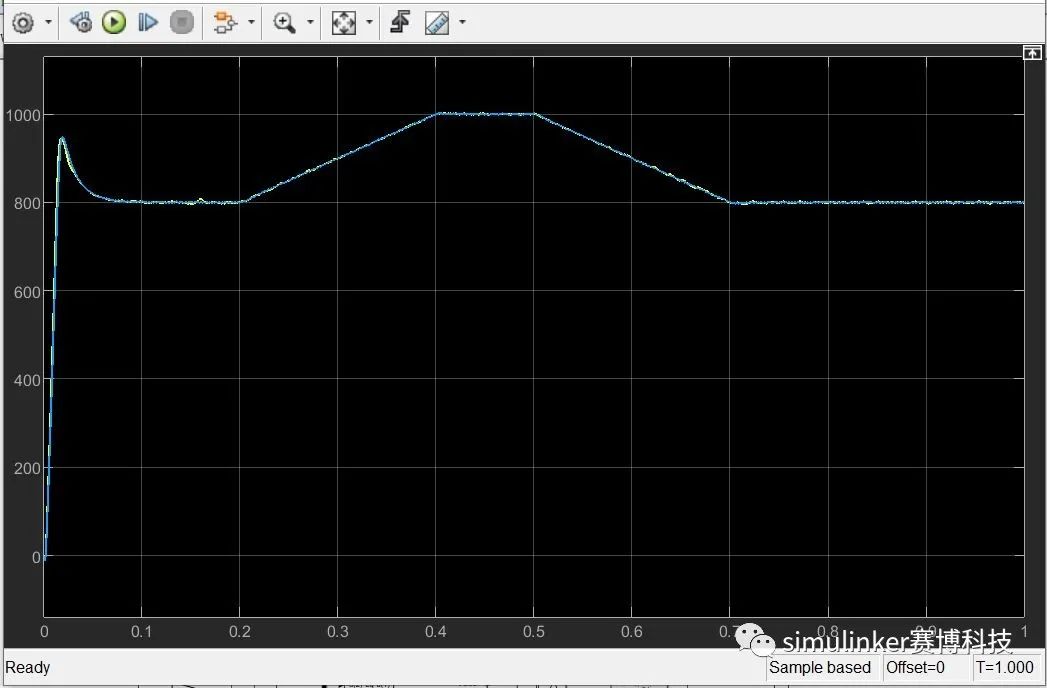
图10 电机转速波形（r/min）

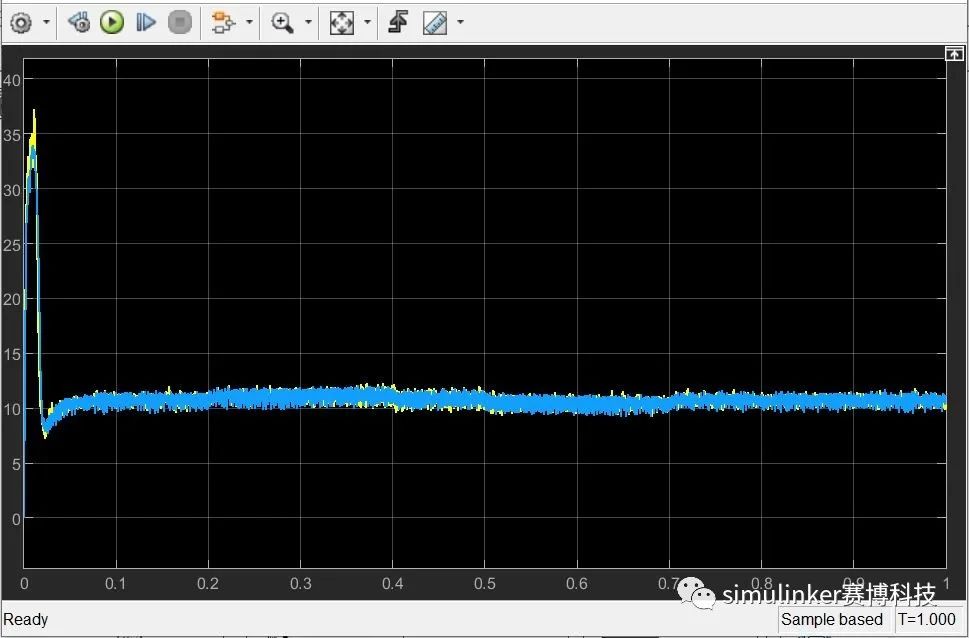
图11 电机转矩波形

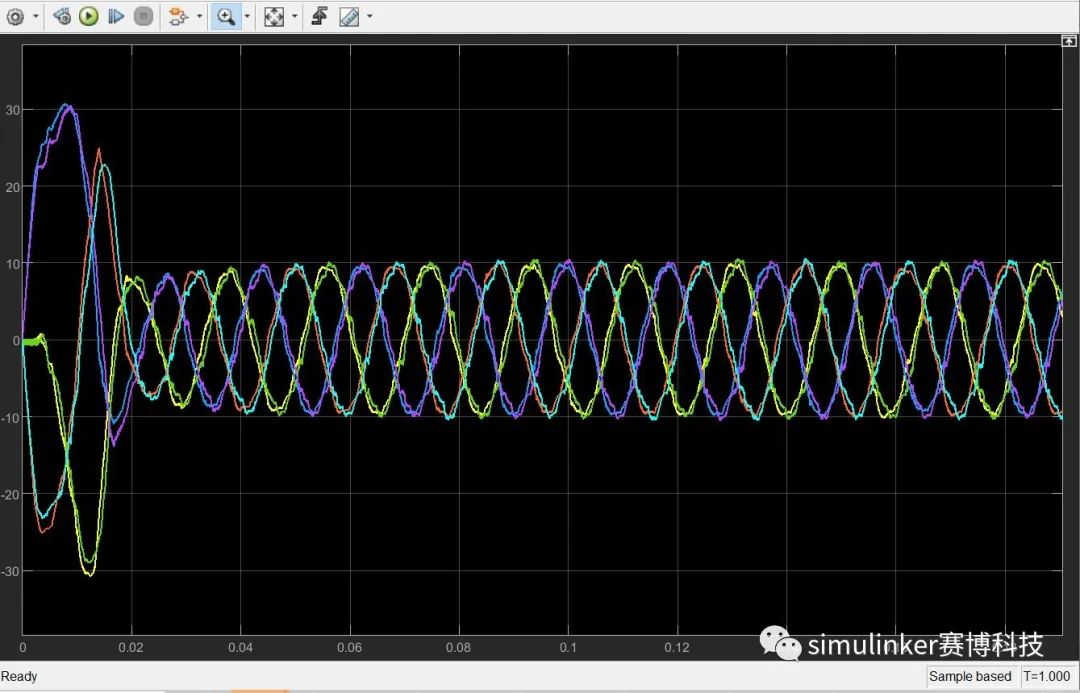
图12 电机电流波形

通过上述仿真结果可以看出，在相同电路拓扑及输入给定的情况下，搭建的永磁同步电机数学模型仿真结果波形与matlab自带的电机模型仿真结果几乎完全重合，验证了模型的正确性。