简介

此KWIK（技术诀窍与综合知识）电路应用笔记提供了解决特定设计挑战的分步指南。对于给定的一组应用电路要求，本文说明了如何利用通用公式应对这些要求，并使它们轻松扩展到其他类似的应用规格。

在任何采样系统中，例如涉及ADC的测量系统中，有一种称为混叠的现象，它可能导致处于较高频带的信号“向下折叠”到奈奎斯特频带，使其与目标信号无法区分。奈奎斯特频率是采样速率fs的一半。由ADC采样的电路带宽应小于采样速率的一半。混叠会导致干扰信号和噪声污染输出，从而影响测量精度。图1和图2分别显示了正确采样（高采样速率）和不正确采样（低采样速率）的例子。

 

图1：采样速率足够高，可分辨信号

 

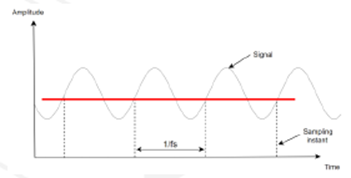
图2：低采样速率，混叠回到DC

有些应用依赖频域中的数据分析，例如状态监控、预防性维护、电力质量监控和被动声纳，对于这些应用中使用的测量系统，混叠是一个特别的问题。这些系统通常支持宽带宽数据采集，能够处理频域中的振动、功率和声学等信号，并根据信号音和谐波的特征做出决策。监控的性质要求使它们对频谱干扰特别敏感。低通滤波器是这些测量系统中的信号链设计的重要组成部分，有助于防止带外信号和噪声折叠到目标信号带宽中。

信号处理电路通常选择有源滤波器，而不选择无源滤波器，原因是有源滤波器提供的输出功率增益和频率范围可通过修改滤波器参数来轻松调整。巴特沃兹、椭圆、贝塞尔和切比雪夫滤波器是四种最常见的有源滤波器。要选择最合适的滤波器，实际上取决于应用和滤波器设计过程中需要权衡的因素，如频率响应、级数或相位线性度。图3显示了每种有源滤波器的响应，设计技巧部分会提供进一步说明。

 

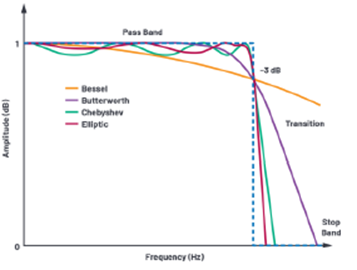
图3：四类有源滤波器

这里选择的是实现巴特沃斯滤波器。一旦选定了滤波器类型，通常用于支持有源极点对拓扑的配置是Sallen-Key滤波器和多反馈滤波器。此KWIK电路笔记将帮助设计和实现低通Sallen-Key滤波器以防止混叠。

单级Sallen-Key滤波器由有源器件（运算放大器）和无源元件（电阻和电容）组成。运算放大器的电压增益由一个双电阻分压器设置，运算放大器用于抑制超范围信号。本文讨论一个针对低功耗应用的滤波器电路设计示例。所讨论的原则适用于一般的滤波器设计。该设计使用10µA电源电流、低IB、零漂移运算放大器LTC2066。我们的低功耗信号链产品系列中还有其他运算放大器可以提供相似的结果（AD8505、LTC6258、LTC2063、ADA4505、MAX40023、MAX40108）。

图4显示了电路的整体原理图，其中选择LTC2066来实现Sallen-Key、双极点、单位增益的低通滤波器。

设计规格示例

低功耗应用通常使用单电源，电源电压通常在1.8 V和3.6 V之间。图4所示电路的设计选择取决于传感器输出和应用要求。对于这种情况，一种可能的传感器是ADLX356B，它是一款加速度计，用于在有许多高频干扰信号的非常嘈杂环境中测量机器的振动。图4中电路的主要设计规格示例列在表1中。

 

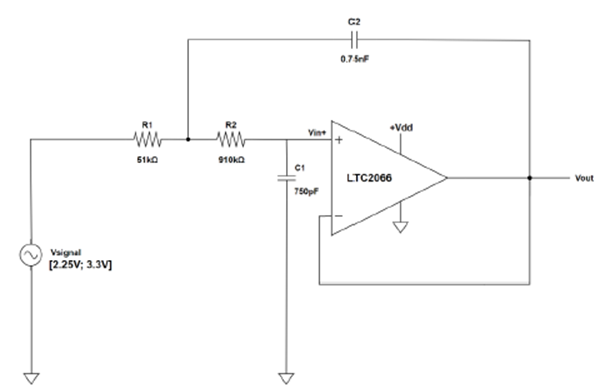
图4：具有单位增益的Sallen-Key低通滤波器

表1.图4所示电路的主要设计规格

设计描述

图4中的电路包括LTC2066，它是一款10µA电源电流、低IB、零漂移运算放大器，可以采用最低3.3V电源VDD供电。LTC2066采用6引脚SC70封装。这种低通Sallen-Key滤波器用于对加速度计的输出进行滤波，以防止混叠到目标频带中。

滤波器的输出表示为Vout，而Vsignal表示加速度计的输出。

设计注意事项

1.图4中的电路是一种单位增益的Sallen-Key滤波器。可将电阻网络添加到运算放大器的反馈回路中，以给电路增加增益（参见附录1）。品质因数Q（衡量稳定性方面的性能）与增益本质上相关。为获得最佳稳定性，增益应低于3。

2.品质因数Q对于Sallen-Key滤波器可能很重要。在此设计中，Q保持√2⁄2，这是巴特沃兹二阶滤波器的标准值。可以调整Q以改变滤波器响应。Q越高（切比雪夫滤波器），滚降速度越快，但相位线性度和幅度平坦度会下降。Q越低（贝塞尔滤波器），相位线性度越好，但抑制性能会下降。其他对于描述低通滤波器很重要的参数可见图5上的标识。

 

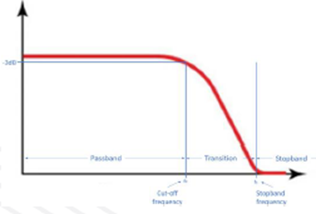
图5：低通滤波器通常的幅频表现

3.与理想的低通滤波器响应不同， Sallen-Key滤波器的响应不会在超过截止频率后持续降低。在截止频率之后，滤波器增益将以40dB/十倍频程的斜率降低，直到某一频率（取决于所选的放大器），然后滤波器增益开始以20dB/十倍频程的斜率提高，直至变成恒定值。这种特性源于以下事实：运算放大器不是理想的，具有有限的增益带宽，并且输出阻抗不是零。在超过其能力的频率时，这种有限的增益带宽会导致运算放大器丧失活力。当发生这种情况时，运算放大器看起来像是连接到地的输出阻抗，因为电容C1和C2表现为短路。

不仅应该监视Sallen-Key滤波器的高频特性，而且必须知道它在什么频率开始再次提高，如图6中的绿色曲线所示部分，而蓝色曲线是理想特性。此限制被称为阻带限制。

 

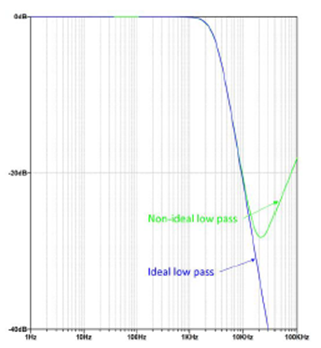
图6：阻带限制

4.在Sallen-Key滤波器中，为电阻和电容选择的值成反比，这意味着如果电阻较大，那么电容将较小。

当传感器不能很好地驱动滤波器时，使用大电阻和小电容会很有用，这样就不会给传感器带来负担。最后，Sallen-Key滤波器引入了一个问题，如设计技巧3所述，其抑制信号的能力在高频时会降低。较大电阻可缓解此问题。

较小电阻和较大电容也有一些好处。小电阻对直流性能有利。输入偏置电流流入运算放大器输入端，因此电阻值越低，直流偏移越低。这种组合还能降低噪声。最后，在较高频率时，小电阻会降低寄生电容对设计的影响。

对于这种低功耗设计，最好使用大电阻和小电容。

5.选择无源元件值（电阻和电容）时，应考虑容差。

例如，当选择R1、R2、C1和C2的值时，这些元件的容差可能会改变滤波器特征，例如截止频率。在多通道解决方案中，元件容差还会影响通道之间的匹配。

设计步骤

1. 设置滤波器的截止频率：

开始设计Sallen-Key滤波器之前，必须考虑传感器规格。对于此设计，加速度计的相关带宽为3kHz，因此Sallen-Key滤波器设计的目标截止频率将设置为fc = 3kHz。

注：依据低通Sallen-Key转换函数计算截止频率的公式为：

 

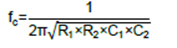
2.设置滤波器的Q：

有多种方法可以实现Sallen-Key滤波器并评估元件的值。在不实施增益的情况下，一种不限制设计的常见方法是使用比率设置这两个电阻和两个电容。也就是说，电阻R1和R2设置如下：

 

而电容C1和C2设置如下：

 

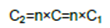
第一步是选择m和n的值。从设计技巧2可知，品质因数Q = √2⁄2 ≈ 0.707，但因为增益K等于1，所以也可以简化来自转换函数的Q因数的表达式：

 

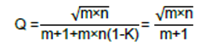
由于未知参数比已知参数多，因此通常固定一个比率。一个常见值是n = 10，此设计过程将使用该值。由于n = 10，现在便可求得m的值。

 

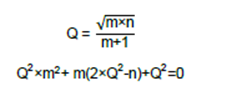
该二次方程的完整求解过程见附录，m的两个解是：

 

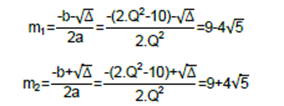
解m1和m2是可以获得√2⁄2的品质因数的两个值。

3.元件值：

根据设计注意事项第4点，期望是在合理范围内使用大电阻和小电容。现在，比率为已知值，下一步是选择R1的值以计算其他元件值。一个合理的高值是R1 = 51kΩ，这是标准电阻值。此值也足够高，使得低功耗运算放大器LTC2066的输出阻抗不至于过大。上一步求得了电阻比的两个解。在Sallen-Key滤波器中，出于阻抗原因，最好将低值电阻放在R1位置，因此将保留m1解。

根据先前确定的R1值和所选的比率，可以计算R2。

 

最接近的电阻标准值为910kΩ。

一旦选定并计算出电阻值，借助截止频率的简化表达式可以计算C的值，然后计算两个电容的值。

 

根据先前的计算，对于C1，最接近的标准电容值为75pF。利用先前确定的比率可以计算C2的值，

 

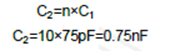
最接近的标准值为0.75nF。

4.阻带限制频率：

考虑设计注意事项第6点，在Sallen-Key低通滤波器的设计中，尽管它是低通滤波器，滤波器增益最终也会再次提高。这种行为来自放大器的输出阻抗与设计的电阻值R1和R2的相互作用。这些电阻的值越高，阻带限制出现得越远。

设计仿真

模拟滤波器向导工具根据用户的规格提供滤波器建议，并辅助设计滤波器（低通、高通和带通）。它还能帮助检索所选滤波器的预期性能，例如幅度、相位、噪声、输入阻抗、静态功耗以及对电路的建议。它也会提供对滤波器的理论预期和实际性能的严谨分析。

使用此工具的第一步是参考目标低通滤波器设计的规格。为了实现仅有一级的二阶滤波器，阻带规格需要满足某些要求。根据阻带的分贝(dB)值的不同，二阶滤波器的频率间隔是不同的。当为不同的阻带dB值选择3kHz的截止频率时，设置二阶滤波器的频率间隔如表2所示。

表2：行为结果间隔

根据设计步骤，通带的特征是0dB增益和3kHz (-3dB)截止频率。在25kHz时，阻带规格将是-30dB。最后，您可以选择滤波器响应，也就是您想要使用哪种滤波器（巴特沃兹、切比雪夫、贝塞尔……）。正如设计注意事项第2点所述，为了尽可能接近上述理论，我们将选择二阶巴特沃兹滤波器。在第一个窗口中，可以看到刚刚输入的规格中的级数，如图7所示。

 

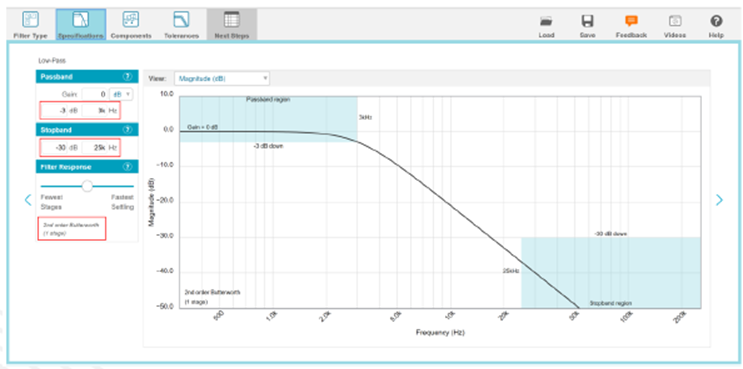
图7：模拟滤波器向导工具的规格窗口

在规格窗口中可以检索幅度视图。这是滤波器在理想条件下的频率输出的样子。在高频时，滤波器的确是不断滚降。

输入规格后，左键单击图8中显示的“components”（元件）按钮。在此窗口中，单击元器件选项卡中的“I want to choose”（我想要选择）之后，不仅可以选择电阻和电容的值，还可以选择运算放大器基准电压源。您还可以选择将滤波器实现为Sallen-Key型还是多反馈型。为了尽可能接近设计步骤，这里选择LTC2066。该工具还会提供电阻和电容的标准值，同样，我们将选择尽可能接近以上计算值的元件。

所有元件设置完毕后，便可监视滤波器的行为，如图8所示。与图7相反，幅度视图这次不是用理想运算放大器来仿真，而是用真实运算放大器来仿真，它在高频时引入了阻带频率。行为结果的摘要如表3所示。

表3.设计目标与仿真交流分析

根据设计步骤、设计目标和模拟滤波器向导的结果，就元件值而言，输出似乎比较相似。

您可以监视其他结果，以便更好地了解ADI工具提供的Sallen-Key低通滤波器，例如功耗或有效值噪声。

 

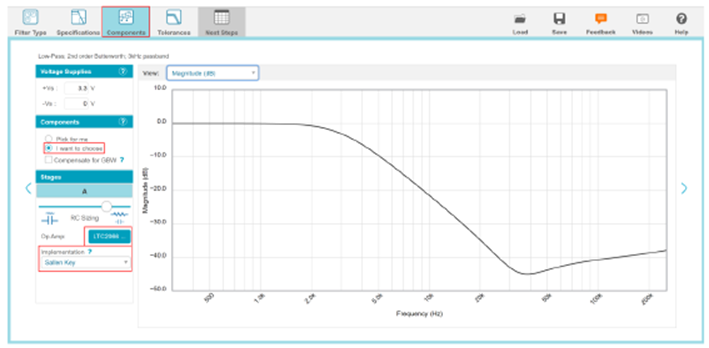
图8.模拟滤波器向导工具：电路结果

LTspice也是一个很好的仿真工具，它能检查上述设计步骤中的计算。LTspice原理图如下图9所示。所做的仿真是电路的频率响应，结果可从图10中检索，输入信号为1V (1kHz)。图10中的光标放在低通滤波器的-3dB点上。表4显示了设计目标与仿真结果的比较。

表4.设计目标与仿真交流分析

虽然截止频率非常接近期望值，但范围的起源不同。首先，电阻值取标准值，但应尽可能接近计算值。该设计显示，在最高80kHz的阻带时，至少为-20dB的衰减。如果这不足以达到设计要求，可以考虑使用更宽带宽的运算放大器，但功耗会提高。另外，可以考虑在Sallen-Key滤波器之后使用一个简单的R/C低通滤波器，以在较高频率下获得更多衰减。

 

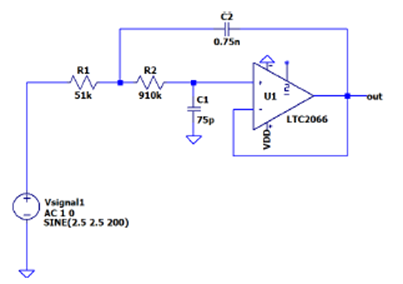
图9：LTspice原理图

 

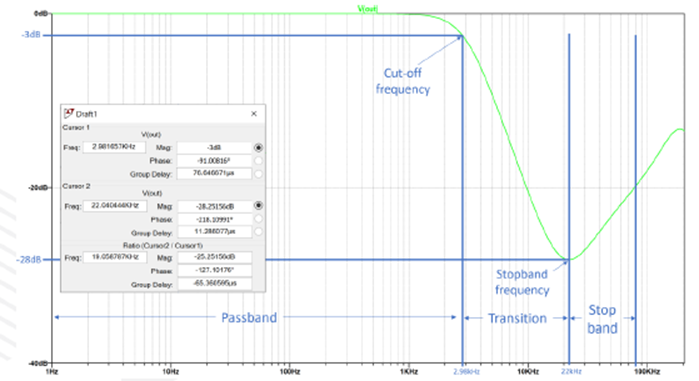
图10.交流仿真结果

设计器件

表5.运算放大器

参考资料

Ltspice

LTspice®是一款高性能SPICE III仿真软件、原理图采集工具和波形查看器，集成增强功能和模型，简化了开关稳压器、线性稳压器和信号链电路的仿真。

模拟滤波器向导

钻石图工具是一款Web应用程序， 可基于Analog Devices 的元器件生成滤波器建议，助您设计出具备所需特性的低通、高通或带通滤波器，且准备时间更短。

附录

附录1：

如果需要增益K，所使用的公式将不相同。品质因数的公式将是：

 

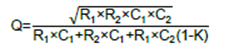
在这种情况下，品质因数和截止频率之间存在关联。为了满足设计规格，同时将元件值设置为先前的比率，设计过程首先应确定增益K，以及电阻和电容的比率m和n以设置Q。然后应设置C值，最后根据期望的截止频率fc计算R值：

 

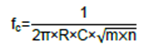
增益K将等于：

 

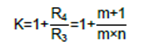
增益可能会改变运算放大器的带宽，进而影响通带和阻带的行为。放大器的输出阻抗须除以环路增益，因此输出阻抗将随频率的提高而上升。较小的R3和R4电阻也会影响滤波器的响应，让阻带频率向高频移动。

 

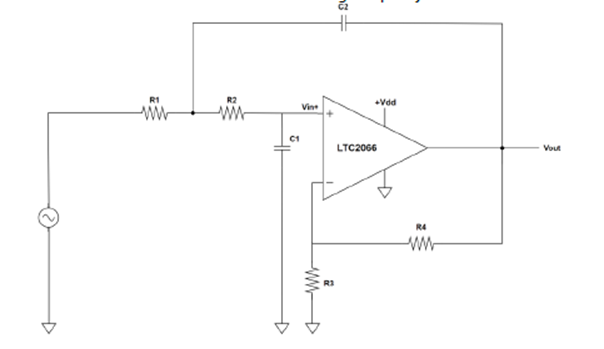
图11.具有增益的Sallen-Key低通滤波器

附录2：

要求解的二阶方程如下所示：

 

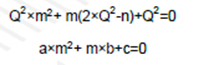
此方程的Δ为：

 

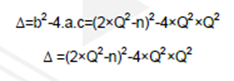
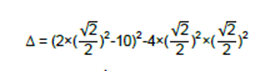
使用n = 10且Q =  ：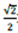

 

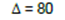
由于Δ大于零，因此有两个解：

 

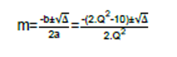
致谢

主要顾问：

David Plourde，科学仪器(SCI)部IC设计工程师

Tim Green，科学仪器(SCI)部高级模拟应用工程师