C-V测量是测定MOS器件特性的主要方法，它广泛地应用于半导体材料的研究中。C-V测量时常常在SiO2中观察到有害的频率离散。用于校正测量误差数据的一些分析公式和模型已得到充分研究。着重于消除串联电阻、氧化物漏电、氧化物与半导体间不希望有的损耗介电薄层、多晶硅耗尽层和表面粗糙度等等的影响。减少纳米级MOS器件中栅极漏电的迫切需求刺激了用高k电介质替代SiON的努力。但是，将高k电介质引入生产线将再次引起C-V测量曲线积累区处的频率离散。到目前为止，频率离散的准确来源仍有待讨论。

本文研究了高k电介质堆层中频率离散的原因。特别提出了电介质介电常数（k值）的频率离散。为了确证单独k值相关影响，对高k电介质和硅衬底间损耗界面层的影响及串联电阻和硅金属背接触的重要性也充分地进行了讨论，并基于双频技术建模。根据实际测得的LaAlO3/SiO2、ZrO2/SiO2和LaxZr1-xO2/SiO2叠层电容值评估它们k值的频率相关性。

器件加工和实验过程

将高k电介质（LaAlO3、ZrO2和LaxZr1-xO2）淀积在n型Si（100）衬底上。高k薄膜和硅衬底间的界面层是～1nm的原始SiO2，由截面透射电子显微镜测得（没有示出）。用1100℃下干法氧化热生长的SiO2样品与高k叠层比较。MOS电容用Au栅热蒸发制造，有效面积为4.9x10-4cm2。所选Si晶圆的背面接触用HF缓冲溶液清洗，接着用热蒸发方法淀积200nm厚的Al膜以使串联电阻影响最小。然后，所有样品在合成气体中400℃退火30分钟，再在1k到1Mz频率范围内用HP4192阻抗分析仪测量。

实验结果和讨论

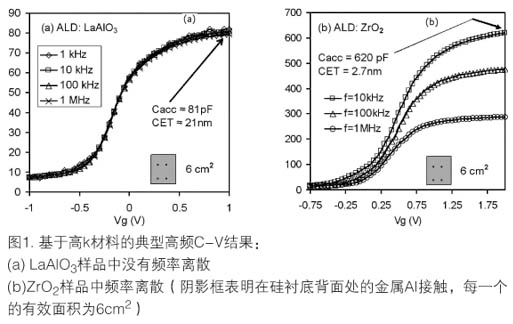
基于高k介质的典型C-V结果分别示于图1（a）和（b）。不管淀积方法、条件和材料如何，有时仍能得到频率离散。产生这一问题可能有三个因素：串联电阻影响，包括不完美的背接触；有损耗界面层的影响（～1nm原始SiO2）；k值的频率相关影响。在讨论k值的频率相关影响前，必需充分研究串联电阻影响和有损耗界面层的影响。

串联电阻影响（通常是由于硅体电阻和不完美的背接触）的重要性在热SiO2 MOS电容中得到最好的展示，其中体电介质与硅衬底间的损耗界面层的影响是可以忽略的。SiO2中频率离散只有在衬底有效面积小的样品中观察到，如图2（a）所示。此外，对于没有Al背接触的小样品，尽管测量条件是同一的，测得的结果也不再重复，如图2（b）所示（闭合的符号）。这就破坏了测量方法的可靠性。

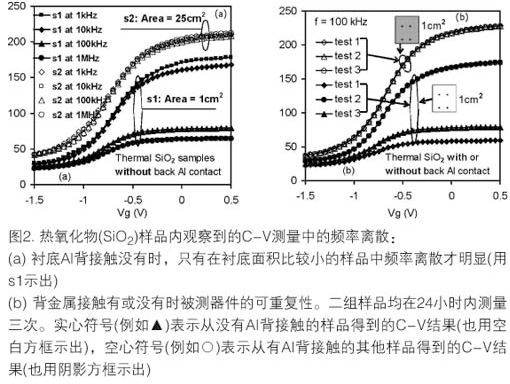
为了在任意测量时间和频率下对SiO2重建测得的C-V曲线，必须考虑可能由背接触不完美和硅串联电阻产生的“寄生”分量。然后对C-V曲线实施校正以得到它们的真实值。图3（a）是理想情况下的等效电路，可与实际测量模式比较，其中Cox代表SiO2栅介质的实际频率自主电容，Rs含有硅衬底的体电阻及不同接触电阻产生的量。背接触不完美也用电容Cp建模。CC、GC、Cm、Gm分别指已校正（没有“寄生”分量 Rs和Cp的影响）或测得的电容和电导。

测得的电容可按照此模型校正而恢复，与测量频率无关，如图3（b）所示。串联电阻影响则可直接用在衬底背面淀积Al膜减至最小（图2（b）中的空心符号和图3（b）中的实线）。这表明，一旦考虑寄生分量时，有可能决定无误差的电容真值，保持测量系统的可靠性。

再研究高k MOS电路上损耗界面层的影响。在图1（b）中，要注意频率离散不是串联电阻影响引起的（因为此样品采用了有效面积大的衬底和Al背接触）。图1（a）中看到的频率离散缺失则可用高k层和界面层的相对厚度解释。图1（a）样品的界面层厚度（~1nm）与电容等效厚度（CET）～21nm比较可以忽略不计，这种情况下，高k层电容比界面层电容小得多（即Ch《《Ci）。但对于图1（b）的样品，尽管有Al背接触和较大的衬底面积，频率离散影响仍是很大的。此时Ch与Ci相当，将频率离散影响归因于界面层电容内的损耗（假定原始SiO2为～1nm），其中，缺陷是由界面位错和ZrO2/SiO2化学突变界面处键合配位中的固有差异引起的。

基于这一解释，图4（a）示出了采用双频技术做出的高k堆叠的4-元素电路模型，以便从损耗重建电容值。

图4（b）是校正后的C-V曲线，在三个完全不同的频率对上相互非常一致，证明模型在寻找电容真值方面是成功的。这表明，有损耗界面层也会影响高k堆叠中的频率离散。有损耗界面层对频率离散的影响也能用较密的SiO2膜（没有示出）替代原有SiO2或用厚得多的等效高k层（图1（a））加以抑制。

最后，考虑串联电阻和有损耗界面层二者的影响，评估LaxZr1-xO2介质的κ值频率相关性。图5（a）示出LaxZr1-xO2/SiO2堆叠中典型的频率离散影响，由于大的Al接触衬底和厚的高κ层，这里的影响现在只与其κ值频率相关性有联系。LaxZr1-xO2、ZrO2、LaAlO3和热SiO2介质的频率相关性也示于图5（b）以便比较。LaxZr1-xO2介质的k 值明显与频率（f）有指数律关系，称为Curie-von Schweidler定律 ，（0≤n≤1），式中指数（n）的值表明介质弛豫程度。当La的x组分为0.22和0.63时，n 值分别为0.981和0.985。产生这一结果可能有二个原因：金属氧化物中自由La+或Zr+离子的离子运动导致介质弛豫；自由金属离子与电子阱复合产生偶极矩而引起介质弛豫。揭示LaxZr1-xO2介质弛豫确切的机理需要做进一步的研究。

结论

频率离散产生的两个原因是损耗界面层和串联电阻和衬底背接触不完美，只有在抑制有损耗界面层和串联电阻及不完美背接触的影响后，才能评估k值的频率相关性。基于两个等效电路模型对这些影响进行分析和建模。研究每一个影响后，在LaAlO3和ZrO2介质中没有观察到k值的频率相关性。但LaxZr1-xO2介质的k值有明显的指数律相关性，可用Curie-von Schweidler定律建模。