一、优化的“本质”

先从滤波讲起~

SLAM首先是一个状态估计问题：在前端中，我们需要从k-1时刻的状态量 出发，推断出k时刻的状态 ，最简单的情况下，状态仅包含位姿，如果用四元数表达旋转的话，状态向量就是7维的（position 3 + orientation 4)。我们用来完成状态估计的信息有：k-1时刻到k时刻之间的运动测量 和k时刻的环境观测 。。 上面部分，我们构建了两个时刻间的优化问题，并可以用各种优化策略取去求解。但相比于滤波方法，这并没有什么优越性，其精度和效率都是等价的。

优化方法真正的优势在于它可以考虑更多时刻的信息，从而大大提升精度。这里得提一下贝叶斯滤波框架的局限：贝叶斯滤波方法依赖马尔可夫性，也即每一时刻的状态仅与上一时刻有关，这就决定了上一时刻之前的测量信息将被丢掉。 优化方法则可以考虑所有时刻的测量信息，上面部分中，我们仅考虑了两个时刻间的误差项，现在，我们把所有过往时刻（1, 2, ... k-1, k）的误差项都添加到目标函数中，我们以所有时刻的状态为自变量，求目标函数（也即总体误差）的最小值，这样就得到了整体的最优状态估计！精度大大提升。当然，由于我们考虑了所有时刻的信息，此时的维度会非常大，并且随着时间的推移维度将越来越大！但所幸，目标函数中的单个误差项并不是与所有时刻的状态都相关，所以求解过程中的相关矩阵会呈现出稀疏性，这就允许我们对高维问题实时求解。 我们也可以只取相近若干时刻的状态进行优化（而非所有时刻），也即构建一个“滑窗”。

在此基础上，更高级的做法是，对滑窗边缘的那个时刻，我们对其进行边缘化处理以使其能够融合更早时刻的信息（而不是把更早时刻的信息直接丢掉），这样，我们就构建了“滑窗优化”，这方面的代表作如VINS。 优化作为一种方法，既可以用于前端，也可以用于后端，甚至你想用的任何地方。用于后端时，通常是全局的优化，也即“考虑所有时刻的状态和所有测量误差项”的优化。发生闭环时，意味着当前时刻的状态 和历史上某一个时刻的状态 之间构建了误差项，由于位姿漂移，这个误差项往往很大！当我们再去对全局误差进行最小化时，我们就需要“微调”全局各个时刻的状态量，以把这个误差“分散”到各个时刻去，从而实现全局误差的最小化。这个“微调”的过程，同样由优化来完成。 因此，从以上各个角度来看，一个现代的SLAM系统，本质上就是一个优化的系统，SLAM本质上就是一个优化问题。而所有的视觉里程计，激光里程计，轮式，imu等等，它们的作用就是构建出一个个的误差项。

一个误差项，也即一个约束。

二、线性化与非线性化优化问题

优化问题本质来说都是最小二乘问题，其关键的地方在于：如何设计与建立SLAM的problem structure：

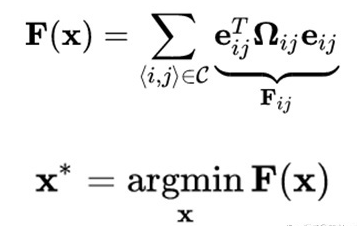
除非理想情况下，实际中都是非线性化问题，但是我们不知道非线性模型，无法求解实际问题，于是我们通过对非线性问题进行线性化分析，忽略一些因素，构建线性化方程求解非线性化问题。

非线性化：1、通俗来说，非线性优化就是求函数的极值，2、再多说一句，在非线性优化里面通常求最小值。

1、我们想求一个 函数的极值问题的时候，线性函数是最简单的，因为是线性的嘛，单调增或者单调减，那么找到边界就可以求到极值。例如 f(x)=ax+b。

2、简单的非线性函数也是很容易求得极值的，例如f(x)=x*x.可以通过求导得到极值点，然后求得其极值。

3、但是对于复杂的非线性函数，或者复杂的数学模型，求导很困难或者无法求导的时候怎么求极值呢？那么就出现了很多非线性优化的算法。来解决对于复杂数学模型的求极值的问题。

三、全局优化与局部优化

全局优化的英文是（global optimization） 1、全局优化是找到在整个可行区域内使目标函数 最小的 可行点x的问题。通俗来说就是从所有可能的x值里面找到最小值 2、通常，可能是一个非常困难的问题，随着参数数量的增加，难度将成倍增加。比如上面的例子是x1和x2两个参数，有着不同的组合方式。那么如何有x1~x100个参数呢，会有多少种组合方式呢？

3、实际上，除非知道有关 f 的特殊信息，否则甚至无法确定是否找到了真正的全局最优值，因为可能会出现 f 值的突然下降，且这个值隐藏在您尚未查找的参数空间中。 局部优化的英文是（local optimization） 1、局部优化是一个容易得多的问题。它的目标是找到一个仅是局部最小值的可行点x：f（x）小于或等于所有附近可行点的f值 2、通常，非线性优化问题可能有很多局部最小值，算法确定的最小值位置通常取决于用户提供给算法的起点。3、另一方面，即使在非常高维的问题中（尤其是使用基于梯度的算法），局部优化算法通常也可以快速定位局部最小值。

四、优化使用的方法

具体的优化求解策略包括最速下降法、牛顿法、高斯-牛顿法（G-N），基于信任区域的L-M法等。

1、梯度下降法

函数的下降方向将永远为函数的负梯度方向 梯度下降法是一个一阶最优化算法，通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。因此指保留一阶梯度信息。缺点是过于贪心，容易走出锯齿路线。

2、牛顿法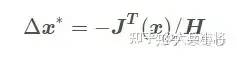牛顿法是一个二阶最优化算法，基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似。因此保留二阶梯度信息。缺点是需要计算H矩阵，计算量太大。

3、高斯牛顿法

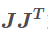
其实其就是使用上式，对牛顿法的H矩阵进行替换

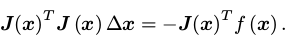
有可能为奇异矩阵或变态，Δx也会造成结果不稳定，因此稳定性差

4、LM信任区域法

但是这个近似假设的成立是有一定程度限制的，我们可以设立一个正值变量△使得模型在一个以x为圆心为半径的圆中被视为可以精确近似。这个圆就是我们所说的信任区域。然后我们就可以基于以下公式求解变化值h。 LM算法大致与高斯牛顿算法理论相同，但是不同于高斯牛顿算法，LM算法是基于信赖区域理论(Trust Region Method)进行计算的。这是因为高斯牛顿法中的泰勒展开只有在展开点附近才会有比较好的效果，因此为了确保近似的准确性我们需要设定一个具有一定半径的区域作为信赖区域。

基于信赖区域我们能够重新构建一个更有效的优化框架 采用信赖区域法我们就需要明确该区域该怎么确定。在LM算法中信赖区大小的确定也是运用增益比例来进行判定的。

四、非线性优化解退化问题

对于SLAM而言，视觉传感器需要纹理信息决定特征点，距离传感器需要空间几何结构信息决定特征点，在特征点缺乏时，状态估计方法会进行退化。定位的退化主要是因为约束的减少，比如NDT需要三个正交方向的约束才能很好的匹配，但若在狭长的走廊上或者隧道环境，条件单一，即使人肉眼观看激光雷达数据，也很难判断机器人所处的位置。因为激光“看到”的环境都是一样的，在隧道方向是没有约束的；并且在隧道中GPS信号是没的，只能依靠高精度的姿态传感器和轮速机的融合来做，当然随着运行时间的增加，误差会慢慢增加。 处理退化的常用方法有: 1）当出现退化时换一种方法;这要求在设计时需要一个备用方法可用 2）在状态估计过程中加入人工约束，如恒速模型的约束。

即使问题本身是可解决的情况下也会带来不必要的误差。我们的方法是在原始问题的部分子空间添加约束。原始问题的解可以分为非退化方向和退化方向，在处理问题时，首先确定退化方向，然后将求出原始问题非退化方向的解，对于退化方向的解使用猜测值。在最后的实践算法中，只使用非线性优化解在非退化方向的分量，不考虑退化方向的分量。 正常情况下，约束应该是分布在空间中的多个方向，从各个角度约束解，如下面所示，绿色点表示问题的解，被非退化约束限制在了一个小区域。这样的解就比较准确，约束发生小变化时，解的变化也很小，被限制在一个局部区域，这样的解就是一个比较理想的解。

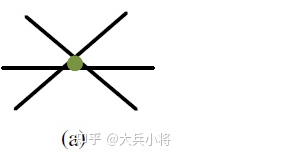
如果解的约束大多近似平行，那么他们就是退化的方向（蓝色箭头表示的方向），这个时候解在退化方向收到的约束就很差。考虑绝对平行时，解的约束也是一个平行的方向，那么这种情况下的解是需要避免的，如果其中一个约束发生了小的偏移，那么解所在的局部区域会发生较大的变化，这样的解是比较糟糕的解。

每次求解时 优化解=原始解在非退化方向投影+估计值在退化方向投影（实际算法中可以将退化方向解丢弃，只考虑非退化方向）