

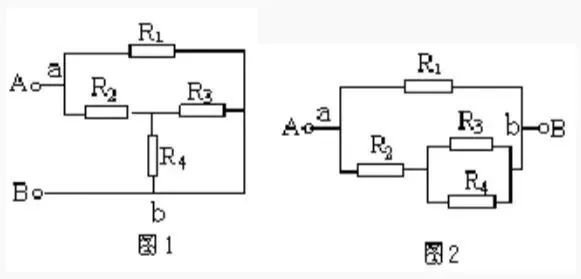
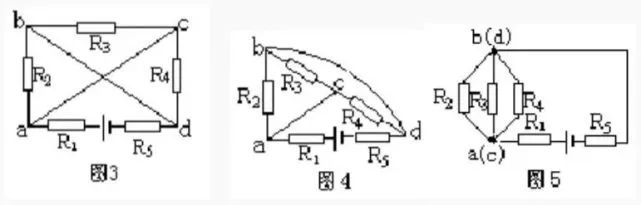
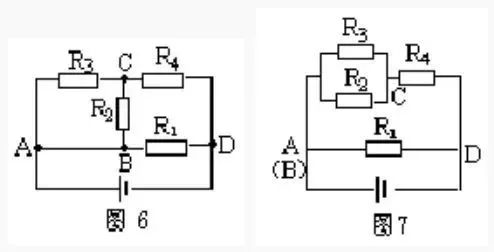
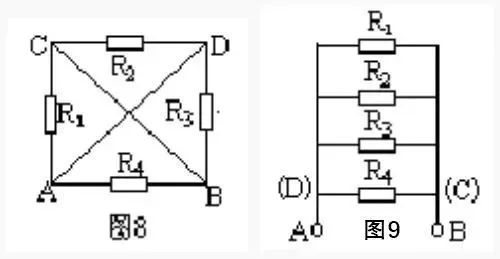
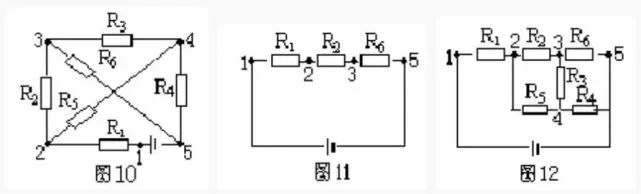
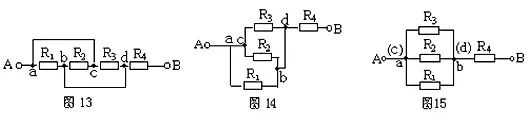
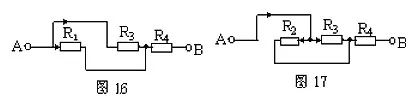
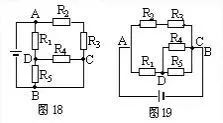
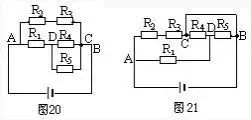
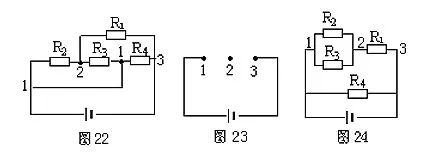
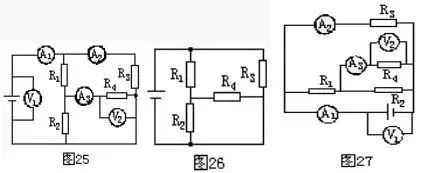

常见电气字母图形符号、实用仪器仪表、实物接线彩图
电流表 :无需断开电路即可测量电流,特别适用于测量大电流或不易接近的导线。 示波器 :用于观察和分析电信号的波形,是电子电路...

全新电路图符号大全,助你快速看懂图
全新电路图符号大全,助你快速看懂图; 电路图,是一种以物理电学标准符号来绘制各电子元器件组成和关系的电路原理布局图,它被广泛应用于人类工程规划和电路研究。通过分析电路图,可以...

仪表电路图识读的基本方法和步骤
各部分工作原理的理解也越深,对每个元器件的作用判断就越准。这样,在仪表检修中才能正确分析故障原因,合理检测并查出故障。因此,仪表工要重视仪表基础知识的学习,不断扩大专业知识面。还要掌握识读电路图的基本方法和步骤,以提高分析电路...


工程师随时可能用得上的10个电路图
中的关键元器件的作用,每个元器件出现故障时电路的功能受到什么影响,测量时参数的变化规律,掌握对故障元器件的处理方法;定性分析电路信号的流向,相位变化;定性分析信号波形的变化过程;定性了解电路...

读懂汽车电路图的输入信号、输出信号、控制信号
方框中所标注的内容一般是整车或系统的一个独立部件。每个方框之间的关系由方框之间的线条沟通,所用箭头表示信息或电量的流向。在分析电路工作原理之前,先阅读该电路的方框图有助于加深了解电路的工作原理。 在分析...

电子制造业SMT电子工程师必须掌握的15种模拟控制电路图!!
。 中级层次 能分析这二十个电路中的关键元器件的作用,每个元器件出现故障时电路的功能受到什么影响,测量时参数的变化规律,掌握对故障元器件的处理方法;定性分析电路...

功率放大器在椭圆超声辅助机械抛光研究中的应用
中,压电陶瓷振子串联一欧姆标准电阻。扫频范围为20k—30kHz。其中当只有间隔的两个电极通电时,振子的B4模态被激励,当四个电极同时通电时,振子的L1模态被激励。 椭圆超声振子谐振特性分析电路图...

示波器眼图如何分辨信号质量
示波器眼图如何分辨信号质量;示波器是很多电子工程师常用的测试仪器,而且高科技的发展,也让示波器开始“进化”,很多高端示波器都会有很多软件,例如示波器眼图软件。当然,如果...
