通过针对制程能力(CPK）分析的学习，分享学习心得给大家参考！

一、X - R 管制图

(一）功 能 :  可以让我们知道制程上的差异,其中有些参数亦可应用在 “ 制程能力 ” 的计算式中. 方便又容易.

条 件 :

1. 先建立制程用之管制图.

2. 将制程变得稳定

3. 然后再评估制程的能力.

（二）作法步骤 :

A. 收集足够资料.  最好能得到制程全部变化数据.

第一阶段需 50 个读值.

第二阶段需 25 个读值.

第三阶段需 25 个读值.

B. 依数据与公式计算出自然管制界限与相关参数.

R 管制图公式 :

二、制程能力

1. 功 能 : 可显示出生产制程的能力是否达到可生产状况.

a. 一般而言 CP > 1.33 时,该制程属平稳可生产.

b. 若 CP < 1.33 时,该制程属不平稳,需小心管制.

c. CP 值愈大显示制程的制造能力愈稳定.  CP 值愈小则显示制程的制造能力愈不足,需要作许多的改善.

2. 制 程 能 力 公 式 :

本公式适用于规格只有设定 上限值 (max 值 ).

本公式适用于规格只有设定 下限值 (min 值 ).

三、Z分布

功 能 :  可提供了解制程的变异与不稳定趋势,预先提出改善预防.

Z 分 布 例子说明:

步骤2：计算出UCL / LCL 超出规格上下限所占之比率

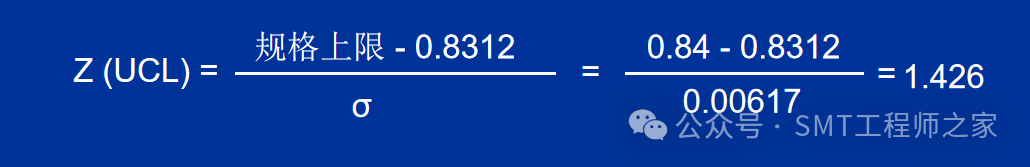
由Z分布表查知 1.426 所占面积约 0.423 = 42.3%

超出规格上限的不良比率 : 50% - 42.3% = 7.7%

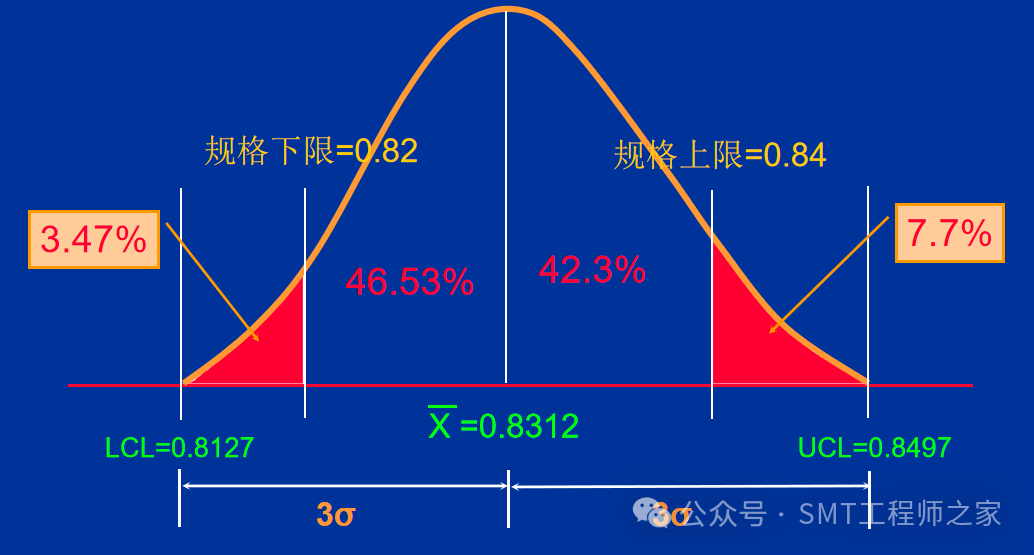
由Z分布表查知 1.8152 所占面积约 0.4653 = 46.53%

步骤3：将超出规格上下限的不良比率相加即等于制程不良率

制程不良率 = 7.7% + 3.47% = 11.17% (估计值)

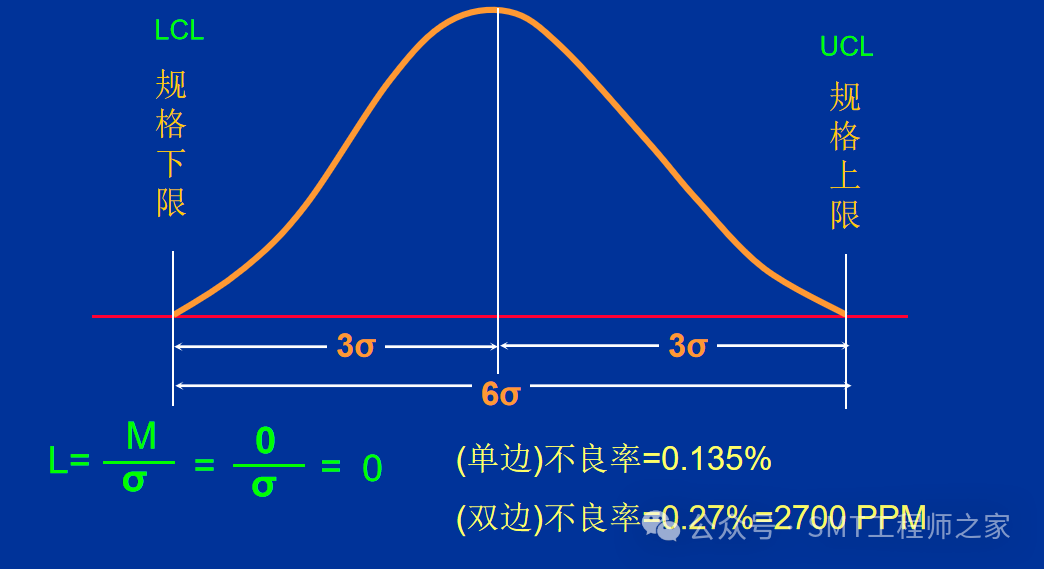
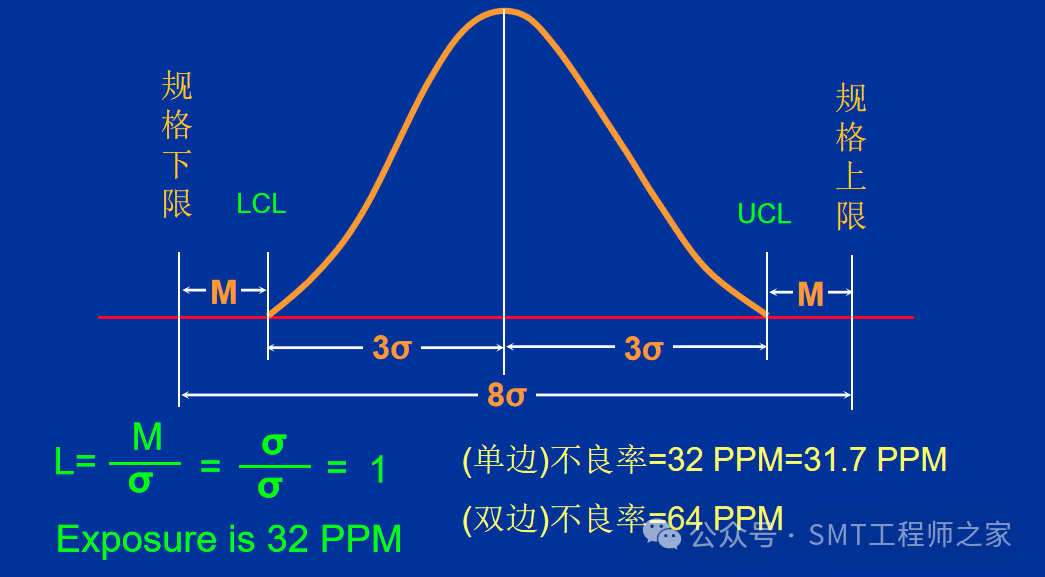
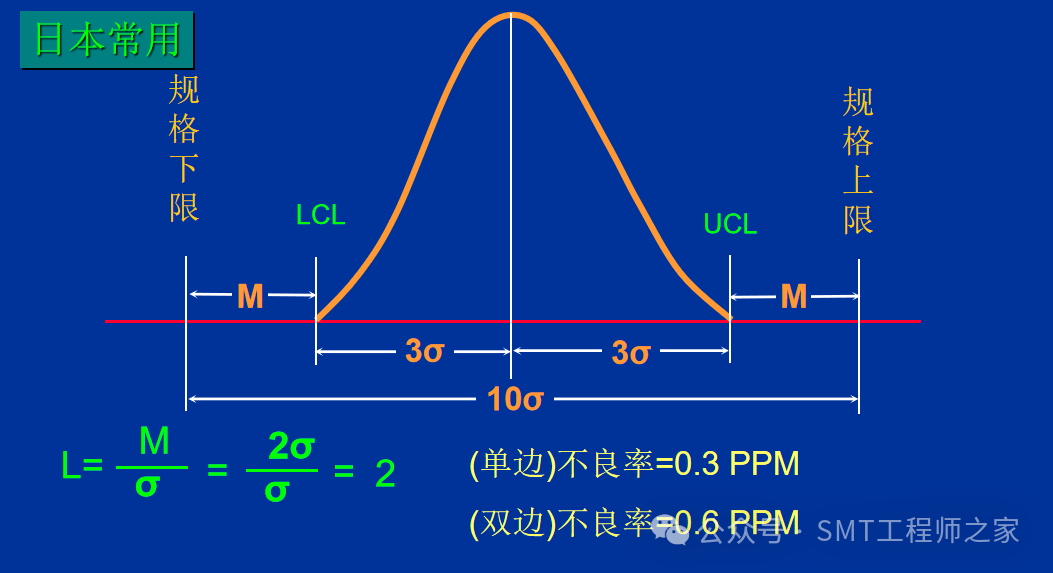
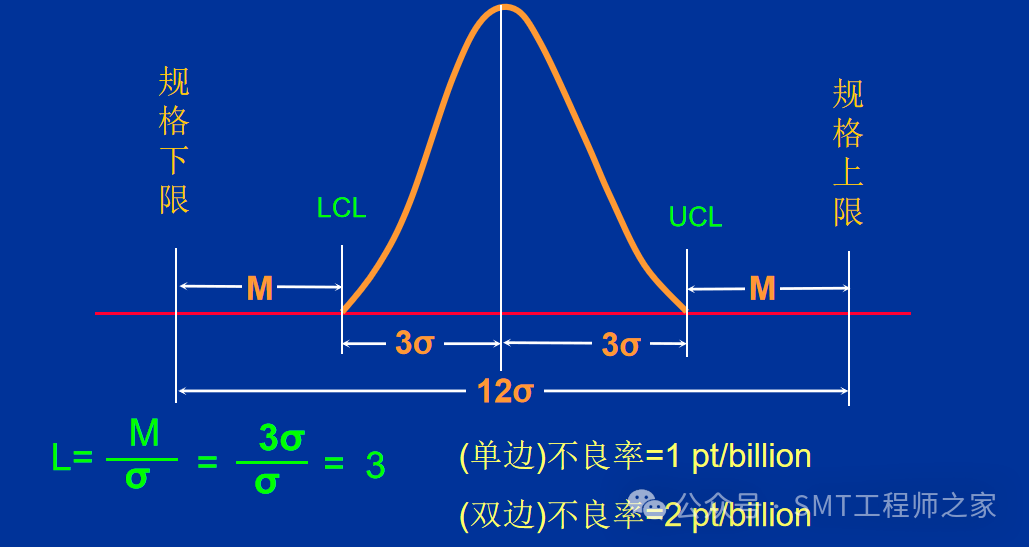
四、制程不良趋势图

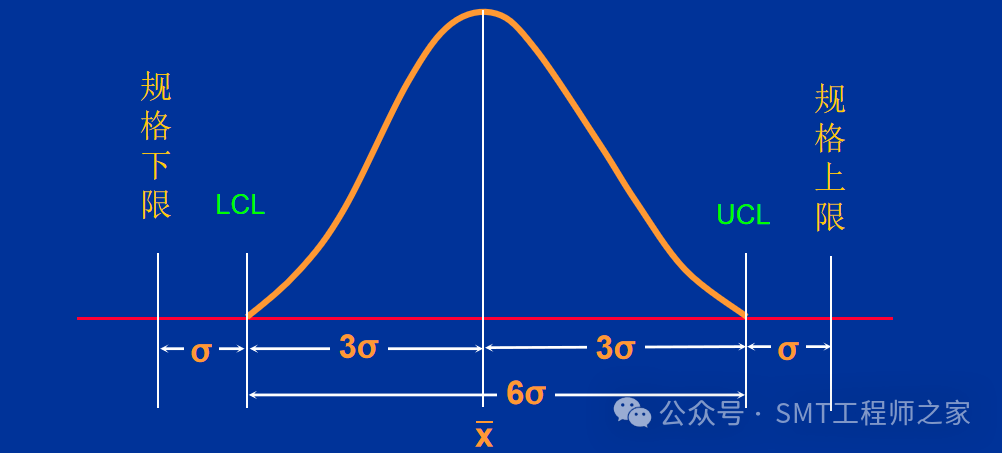
UCL及LCL都在规格上下限之内,且距离规格上下限皆有一个δ以上,此种状况正表示制程能力很好,且非常稳定.

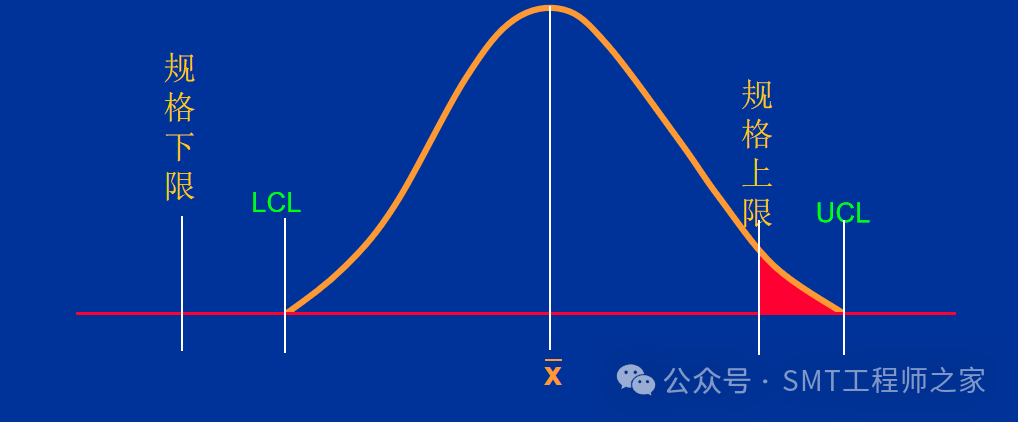
此图表示,制程有变异存在,整个分布图往规格上限偏移,致使UCL超出规格上限, 以致有不良会产生.