在本文中，我们学习了噪声参数，并使用为指定的增益设计单边低（LNA）。

在接收器应用中，信号链中的第一个放大器对整个系统的噪声性能具有主导作用。该放大器应具有尽可能低的噪声系数，同时提供可接受的高功率增益。因此，这种低（LNA）的设计过程应考虑增益和噪声性能。

在本文中，我们将学习如何根据这些要求设计单向LNA。我们将首先探索如何在RF应用中指定双端口网络的噪声参数，然后设计一个能够实现特定增益和特定噪声水平的单向放大器。最后，我们将使用本系列上一篇文章中介绍的RF设计软件对我们的设计进行测试。

二端口网络的噪声参数

正如我在噪声系数度量中详细讨论的那样，电路的输出噪声在很大程度上取决于其源阻抗。同时，连接到源导纳YS = GS + jBS晶体管的噪声系数（F）由以下方程给出：

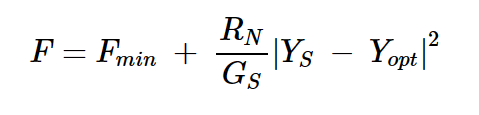
方程式1

其中：

Fmin 是设备的最小噪声系数

RN是设备的等效噪声电阻

Yopt是最佳源导纳

GS是源导纳YS的实部。

从这个方程中我们可以看到F如何随着源导纳（YS）而变化。观察到当YS=Yopt时，噪声因子降低到其最小值Fmin。

Fmin、RN和Yopt的量称为晶体管的噪声参数。我们不计算这些参数，而是由制造商给出或通过测量获得。Fmin有时以dB为单位表示为NFmin，它随着晶体管的偏置点、温度和操作频率而变化。RN参数是一个灵敏度因子，表明噪声因子随着源导纳远离Yopt而增加的速度。

在低频时，Yopt是实数，但对于大多数有源器件，在50至100 MHz以上，它变成了一个复数值。对于任何给定的双端口网络，我们可以找到一个使噪声系数最小的Yopt值。请注意，方程1中没有出现S参数。事实上，器件的S参数没有为我们提供任何有关其噪声性能的信息。

如前所述，F是噪声系数。它以线性形式表示。噪声系数缩写为NF，是转换为dB的噪声系数。因此，F和NF之间的关系可以表示如下：

方程式2

在实践中，确定NF对源阻抗的依赖性需要专门的噪声测量设备。该设备使用短截线调谐器向设备施加一系列复杂的阻抗，然后对这些测量值进行分析，以在ΓS平面上产生恒定的NF轮廓。

图1显示了假设设备的恒定NF轮廓。正如我们稍后将更详细讨论的那样，这些轮廓是圆形的。

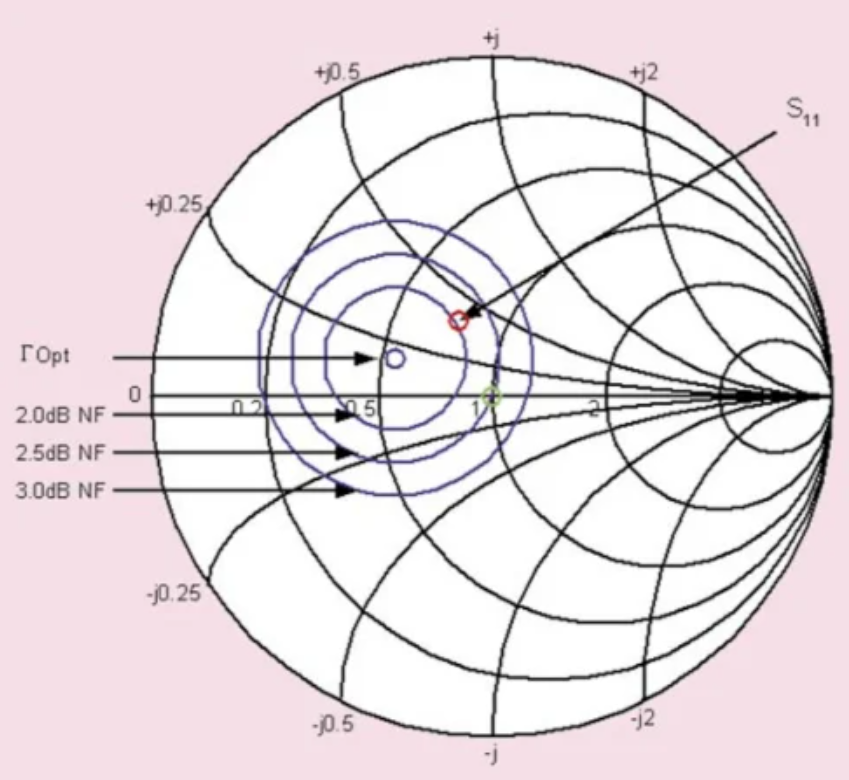
图1.显示了假设设备的NF轮廓，展示了驱动点阻抗对噪声系数的影响。图片由D. Boyd提供

请注意，常见的噪声系数分析仪和网络分析仪无法产生这些NF轮廓。

噪声系数方程的另一种形式，上述引入的RN参数也可以指定为电导项，

$G_N=\frac{1}{R_N}$此外，除了指定最佳导纳外，还可以通过指定等效最佳源阻抗($Z_{opt}=\frac{1}{Y_{}}$)代表时间

(Γopt)或其关联的最佳源反射系数（Γopt）。参数Yopt和Γopt由以下方程式相关联：

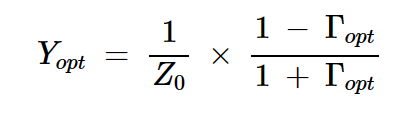
方程式3

使用Γopt参数，方程1也可以表示为：

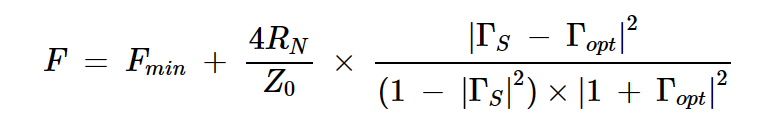
方程式4

请注意，放大器的负载反射系数（ΓL）没有出现在方程4中。由此我们可以看出，输出匹配对噪声系数没有任何影响。然而，匹配的输出可以提供更多的增益，并减少后续级噪声的影响。

放大器的增益和噪声性能之间通常存在权衡关系——在最大增益下无法实现最小噪声。

绘制常数NF圆

为了在给定的噪声系数（F）下绘制恒定的NF圆，我们首先找到噪声系数参数（N）。这由下式给出：

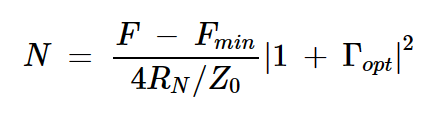
方程式5

常数NF圆的圆心（cF）由下式给出：

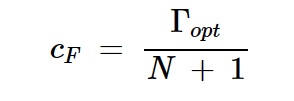
方程式6

通过以下公式计算其半径（rF）：

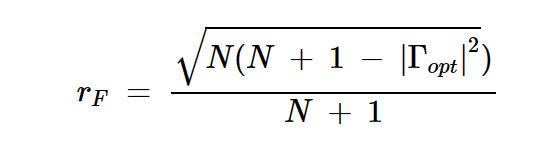
方程式7

为了巩固这些概念，让我们通过一个例子来学习。

示例 1：绘制常数 NF 圆

假设晶体管的Z0 = 50 Ω，f = 1.4 GHz，其S参数如下：

表1.示例晶体管的S参数。

该装置的噪声参数为：

NFmin=1.6dB

Γopt  = 0.5 ∠ 130 度

RN =20Ω。

让我们绘制这个晶体管在NF = 2 dB、2.5 dB和3 dB时的常数NF圆。表2总结了所需的计算。请注意，我们的方程式使用F，而不是NF，所以我们不能直接将噪声系数值代入方程式。相反，我们必须将它们从分贝测量值转换为表示噪声系数的线性项。

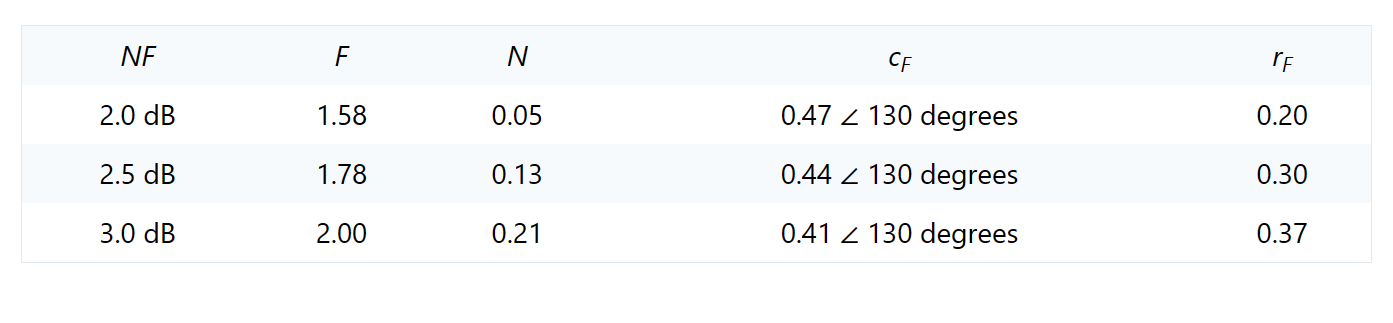
表2。这些计算结果使我们能够为我们的示例晶体管绘制恒定NF圆。

这些恒定的NF圈在图2中绘制。

图2:示例晶体管的恒定NF循环。图片由Steve Arar提供

请注意，恒定噪声圆圈的中心位于从中心到点Γopt的直线上（参见方程6）。在Γopt处，我们得到NFmin = 1.6 dB，噪声圆圈转变为一个点。随着噪声系数的增加，圆圈的中心向原点移动，其半径变大。

设计用于增益和噪声的双边RF放大器

在ΓS 平面中绘制恒定的 NF 圆，可用于找到给定噪声系数下的适当源端接。为了同时考虑噪声和增益，我们还需要在ΓS 平面中绘制增益轮廓。在单边器件的情况下，这是很简单的，其中输入和输出匹配部分的增益是相互独立的。我们将在下一篇文章中介绍双边 LNA 的设计。

示例2：为特定增益和噪声性能设计单边LNA

使用前一个示例中的晶体管，让我们设计一个具有2.5 dB噪声系数和最大可能增益的放大器。

该晶体管具有较小的S12，表明它可能被视为单向的。应用单向品质因数（U），我们得到：

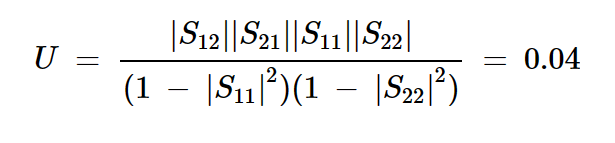
方程式8

由于U小于0.1，我们立即知道单边方法的误差小于±1 dB。因此可以应用单边方法。我们还可以计算出单边近似误差界的确切值。计算结果为：

方程式9

这意味着我们最终设计的实际增益误差应小于±0.35 dB。

接下来，我们确定GS，max，单边器件输入匹配部分的最大可能增益：

方程式10

这转换成1.46dB。

这使我们能够为我们的恒定增益圆选择合适的值。在这个例子中，我任意选择了绘制GS = 0.5、1、1.28和1.4 dB的圆。这些恒定GS圆的中心和半径如表3所示。

表3.恒定GS圆的圆心和半径。

图3绘制了这些圆圈和ΓS平面中NF = 2.5 dB的圆圈。

图3.ΓS平面中的恒定GS和NF圆。图片由Steve Arar提供

在ΓS = 0.45 ∠ 169.17度时，GS = 1.28 dB增益圆仅与NF = 2.5 dB的噪声圆相交。任何更高的GS值都会使我们远离Γopt，从而导致更大的噪声系数。

对于输出部分，我们选择共轭匹配以最大化增益。这导致：

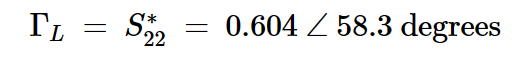
方程式11

并且：

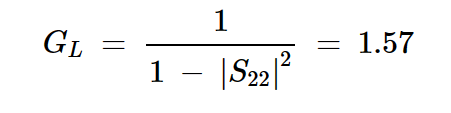
方程式12

这转换成1.96dB。

总增益计算如下：

方程式13

上式中G0 =|S21|2 。这是晶体管基于Z0的传感器功率增益。

接下来，我们使用Z Smith图来设计输入和输出匹配网络。对于输入匹配部分，我们在图4的Smith图中定位ΓS，并通过沿恒定|ΓS|圆旋转180度找到其关联的归一化导纳（yS）。

图4.恒定的|ΓS|圆。圆上的重要点用蓝色标记。图片由Steve Arar提供

从现在开始，我们将史密斯圆图解释为Y史密斯圆图。我们需要一个电路，从位于50Ω终端的圆图中心到yS。恒定|ΓS|圆与1 + jb圆的交点标记为点A，其电纳约为j1。

在设计双端口网络的输入匹配部分时，我们在50Ω终端上添加了一个长度为l1=0.125λ的并联开路短截线，以产生电纳j1。然后，我们添加了一个长度为l2=0.103λ的串联线路，沿着恒定的|ΓS|圆到yS。

输出匹配部分可以以类似的方式设计。如图5所示，输出匹配网络需要长度为l3=0.157λ的开路短截线和长度为l4=0.243λ的串联线。

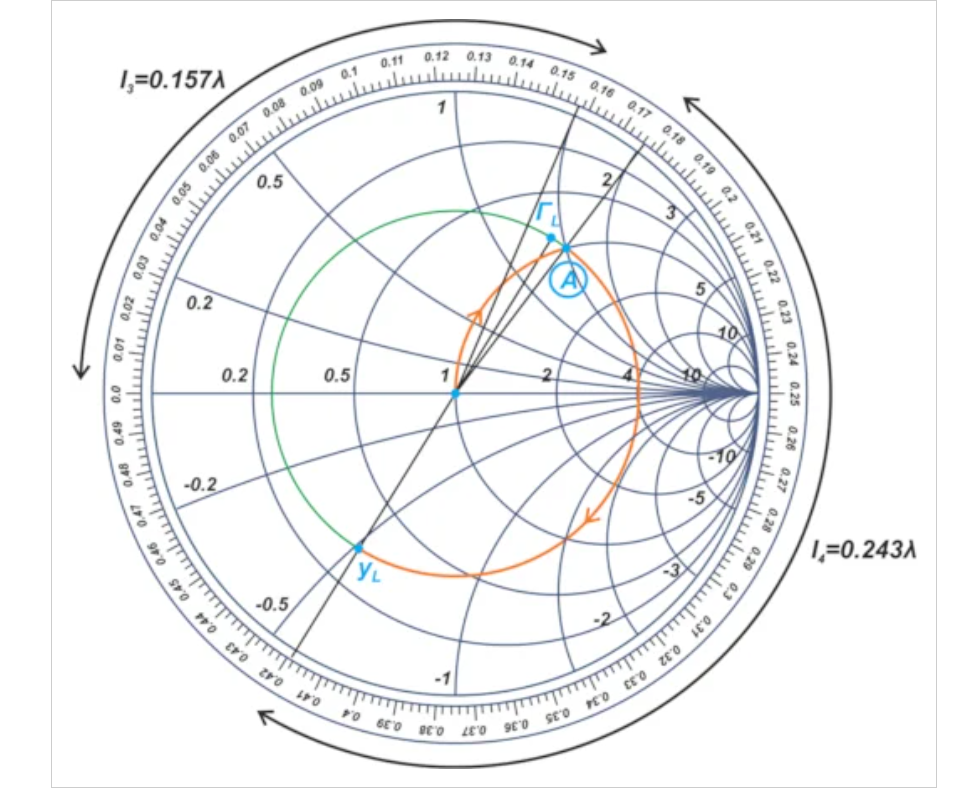
图5.恒定|ΓL|圆。注意l3和l4的值。图片由Steve Arar提供

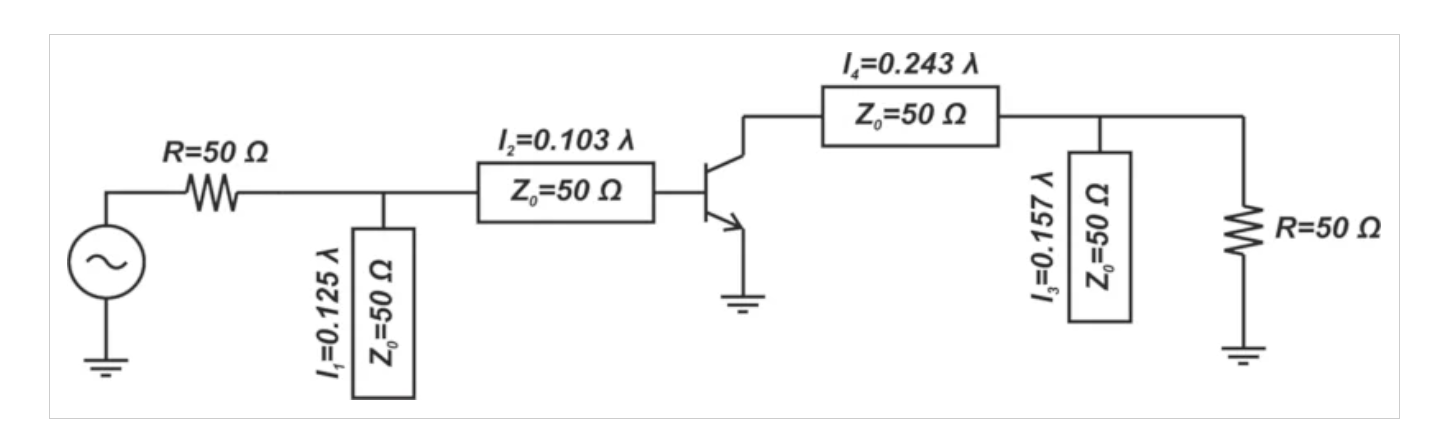
图6.示例LNA的最终设计。图片由Steve Arar提供

现在我们可以使用设计软件来验证电路的性能。

将噪声参数添加到试金石文件

正如我们在最近关于射频放大器稳定技术的文章中所了解到的，Touchstone（.s2p）文件格式通常用于射频设计软件中，以指定双端口网络的S参数。表4显示了图6中放大器S参数的.s2p文件。噪声参数也包含在文件的末尾，尽管这是可选的。

表4.图6中放大器的S参数和噪声参数，保存为Touchstone文件。

图6显示了最终放大器设计的交流原理图。

回想一下，以#标记开头的选项行包含标题信息。此标题信息指定了S参数的频率单位和数据格式。选项行中的术语“R 50”表示S参数的负载终端电阻为50Ω。以！符号开头的行是注释行。

正如你所看到的，噪声参数没有单独的选项行。为了让模拟器能够区分S参数数据结束和噪声数据开始的位置，噪声参数的第一个频率必须小于或等于S参数的最高频率。

噪声信息的数据格式如下：

第一列指定频率（1400 MHz）。

第二列给出了最小噪声系数，单位为dB（1.6 dB）。

接下来的两列给出了最佳反射系数（Γopt = 0.5 ∠ 130 度）的幅值和相位。

最后一列是有效噪声电阻（RN = 20 Ω），归一化为我们在选项行中定义的系统阻抗。

将上述.s2p文件链接到Pathwave ADS中的s2p组件，我们可以分析系统的增益和噪声性能。我们生成的Pathwave ADS原理图如图7所示。

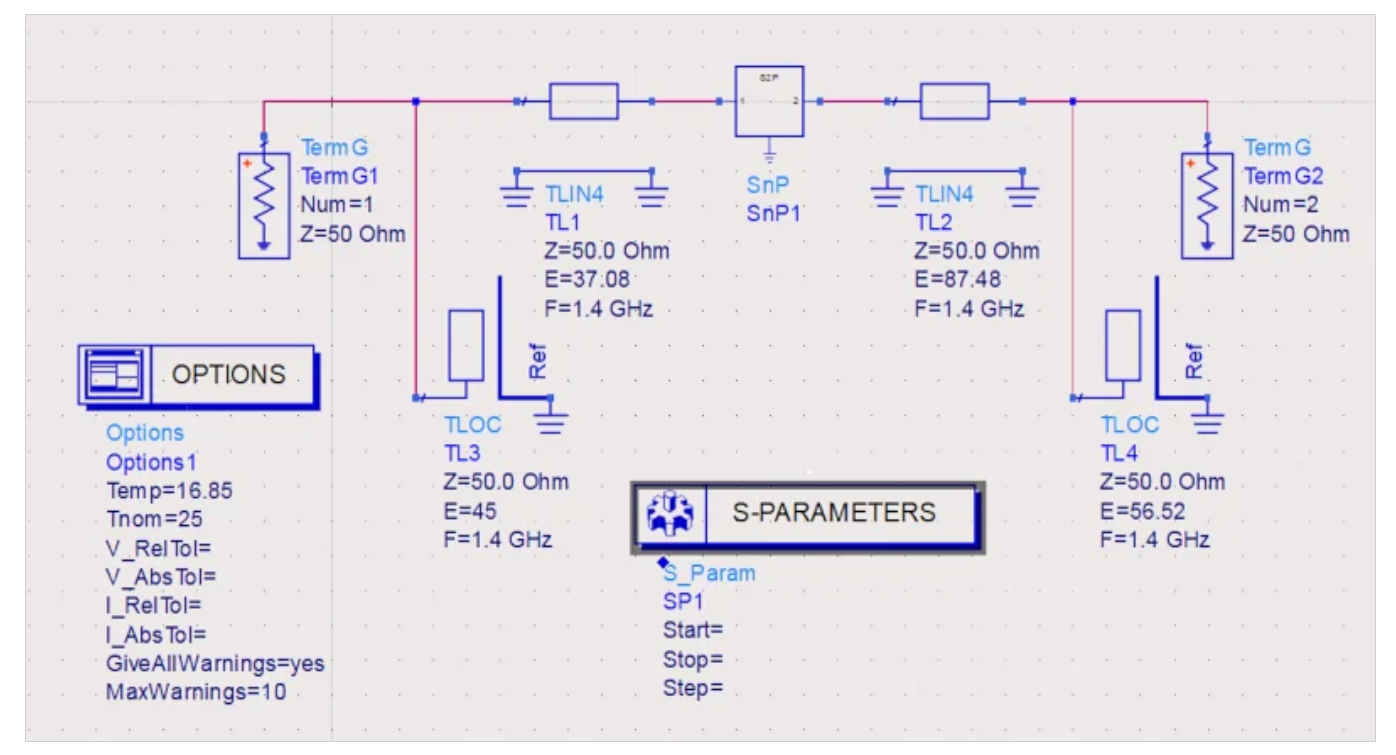
图7.示例放大器的路径波ADS示意图。图片由Steve Arar提供

请注意，模拟温度设置为16.85°C，以确保噪声系数测量与IEEE对噪声系数的定义一致。计算机分析表明，我们设计的电路增益为12.466 dB，噪声系数为2.522 dB。这些数字与我们的设计规格非常接近。

总结一下

本文的后半部分侧重于通过示例进行工作。如果您想复习一下，这里简要总结了前面介绍的概念：

给定工作条件下双端口网络的噪声性能可以通过其噪声参数来充分表征：Fmin（或NFmin）、Γopt和RN。

在ΓS平面中绘制了恒定的NF圆，可用于为给定的噪声系数找到合适的源端接。

为了同时考虑噪声和增益，我们还需要在ΓS平面中绘制增益轮廓。如果设备是单边的，则这是很简单的。

请注意，如果设备是双边的，则在 ΓS 平面绘制增益轮廓就不那么简单了。我们之前使用工作功率增益 (GP) 圆来设计一个特定增益的双边放大器，但 GP 圆在 ΓL 平面内，并不能直接指定可用的源端接。

幸运的是，有一种基于可用功率增益（GA）概念的方法，可以让我们在ΓS平面中绘制双边设备的增益轮廓。我们将在下一篇文章中讨论如何使用恒定GA圆来设计双边放大器，以实现增益和噪声性能。