技术咨询
代买器件
商务客服
研发客服主要有三种类型，即 AND 门、OR 门和 NOT 门。每种都有自己不同的逻辑功能。因此，在这些基本的帮助下，我们可以得到任何逻辑函数或任何布尔或其他逻辑表达式。
本文引用地址：基本逻辑门的真值表：
了解每个逻辑门的功能对熟悉转换非常重要。
1.NOT 逻辑门：
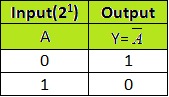
这种逻辑门是数字逻辑电路中最简单的一种。该逻辑门只有两个端子，一个用于输入，另一个用于输出。门的输入是二进制数，即只能是 1 或 0。逻辑门输出端的输出总是与输入端相反，也就是说，如果输入端为 1，则输出端为 0，反之亦然。
可能出现的级数由 2ª 计算得出（输入数由 "a "计算得出）。
NOT 栅极的真值表如下 -NOT 栅极真值表
2.AND 逻辑门
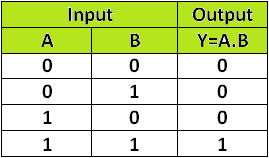
这种逻辑门由两个输入端和一个输出端组成。这种逻辑门的工作原理是，当且仅当两个输入端都是二进制 1 时，我们才会在输出端得到二进制 1。如果任一输入端为二进制 0，则输出端为二进制 0。
可能的相位数 = 2n =22 = 4。
AND 门的真值表如下 -AND 门 - 真值表
3.OR 逻辑门
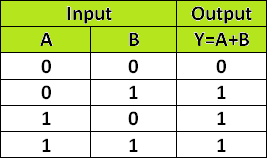
与 AND 逻辑门一样，OR 逻辑门也是一种基本逻辑门，它有两个输入端和一个输出端。如果任一输入端处于低电平阶段，即二进制 0，那么输出端将为高电平，即二进制 1。如果只有两个输入端都处于二进制低电平阶段，则输出将是二进制低电平。
可能的相位数 = 2n =22 = 4。
OR 门真值表如下 -OR 门 - 真值表
4. 门：
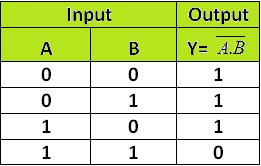
逻辑门是 NOT 逻辑门和 AND 逻辑门的组合。因此， 门由 AND 门和反相门组成。这些门的工作原理是，只有当两个输入端都处于二进制低电平状态（即 0）时，我们才能在门的输出端得到二进制 1；而如果任何一个输入端处于二进制高电平状态（即 1），那么我们得到的输出将是二进制低电平状态（即 0）。
NAND 逻辑门的表达式和真值表如下所示
将 NAND 门转换为其他基本门：
1. 用 NAND 门构建 NOT 门：
用 NAND 栅极构建 NOT 栅极
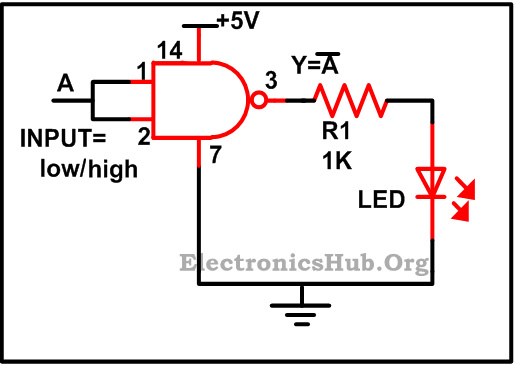
我们只需要一个输入端，因此 NAND 门的两个输入端都被短路，如上图所示。现在，当我们在输入端输入二进制 1 时，由于 NAND 逻辑门的特性，输出端将得到 0，这可以从 NAND 逻辑门的真值表中看出。
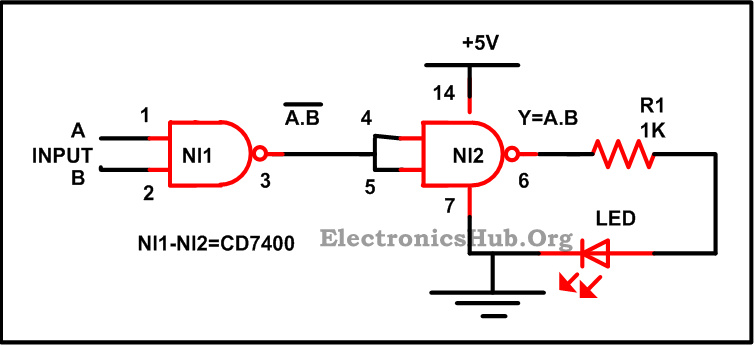
2.使用 NAND 门构建 AND 门：
使用 NAND 逻辑门构建 NOT 逻辑门
3.使用 NAND 逻辑门构建 OR 逻辑门：
使用 NAND 栅极构建 OR 栅极
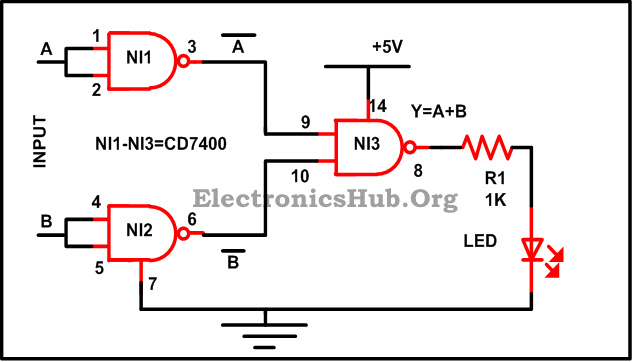
在熟悉这些之前，我们应该先熟悉摩根定理，它指出积的补数等于补数之和。
(AB)‾ = A‾ + B‾ —- EQ 1
如上图所示，使用了两个 NAND 门，每个门的输入端都很短，因此输出为 = A‾B‾
现在将此输出给另一个 NAND 门，得到的输出为-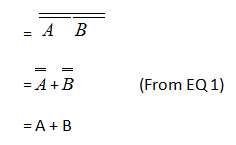
所需元件
CD7402 - 1
R1 (1K) - 1
LED - 1
相关文章
